二叉树基本概念
1 定义
二叉树是由 n(n≥0)个节点组成的有限集合,具有以下特性:
- 空集是一棵二叉树;
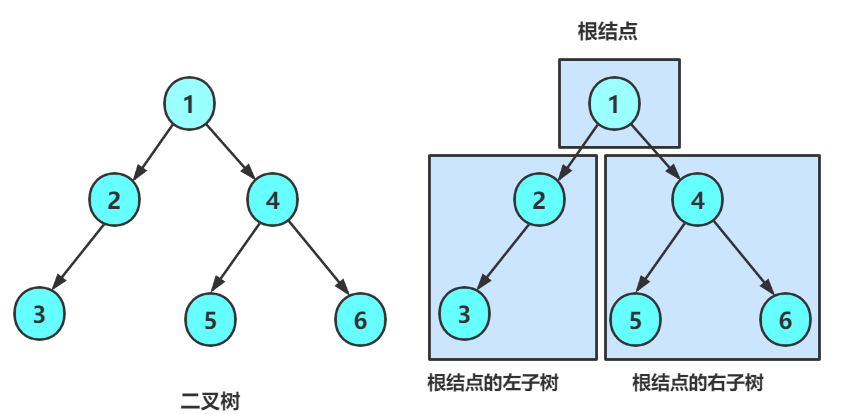
- 非空二叉树由根节点、左子树和右子树组成,且左、右子树均为二叉树;
- 二叉树中每个节点的度(子树个数)不超过 2,且子树有左右之分(有序树)。
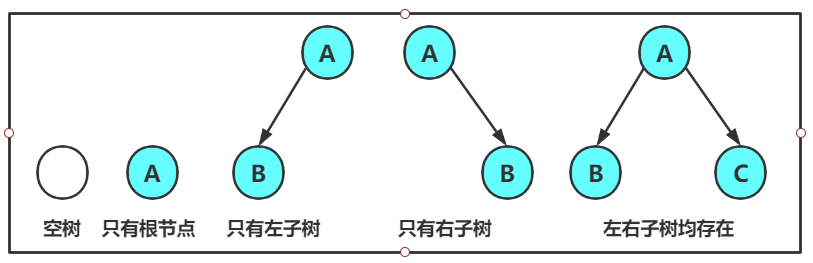
注意:对于任意的二叉树都是由以下几种情况复合而成的:
2 特殊二叉树
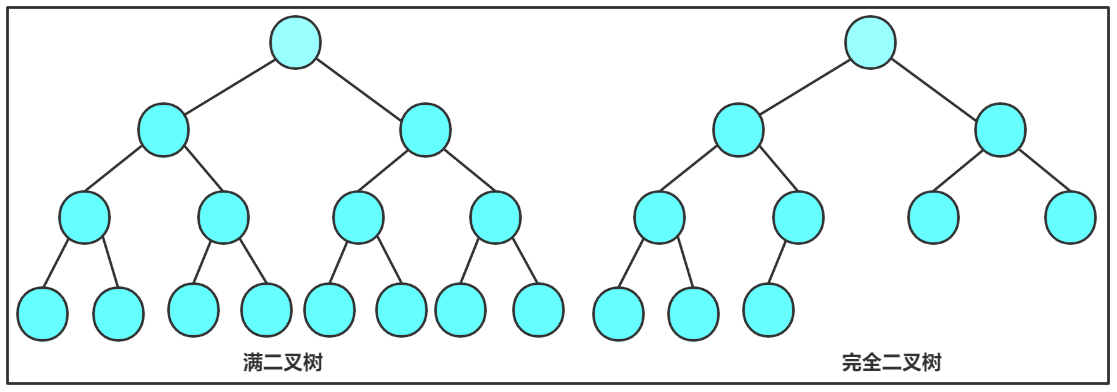
- 满二叉树:每一层的节点数达到最大值,若层数为 k,则节点总数为 2ᵏ-1。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
换一种说法:
设二叉树的层数为 h,也就是说,前 h-1 层都是满的,最后一层不满,而且从左到右都是连续的。中间的左右孩子在结束前,不可以空。
 满二叉树:
满二叉树:
| 层数 | 节点数 |
| 1 | 2^0 |
| 2 | 2^1 |
| …… | …… |
| h | 2^(h-1) |
F(h) = 2^0 + 2^1 + …… + 2^(h-1) = 2^h-1
当有 n 个节点时,可以推算出公式:
3 重要性质
- 第 i 层最多有 2ⁱ⁻¹ 个节点(根节点为第 1 层)。
- 深度为 h 的二叉树最多有 2ʰ-1 个节点。
- 对于任意二叉树,叶节点数 n₀ = 度为 2 的节点数 n₂ + 1。
- 具有 n 个节点的完全二叉树,深度 h = ⌊log₂n⌋ + 1。
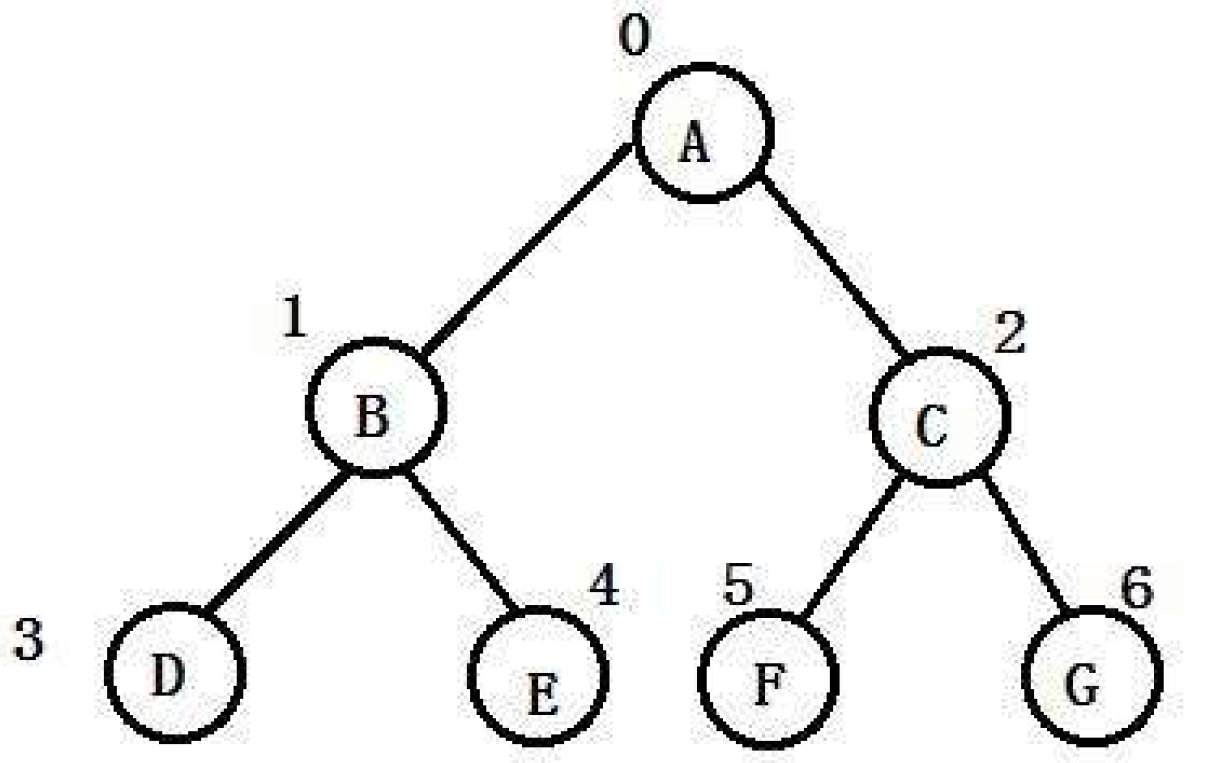
- 完全二叉树按层序编号(从 0 开始)时,对序号为 i 的节点:
- 父节点序号:(i-1)/2(i>0);
- 左孩子序号:2i+1(若 2i+1 < n);
- 右孩子序号:2i+2(若 2i+2 < n)。
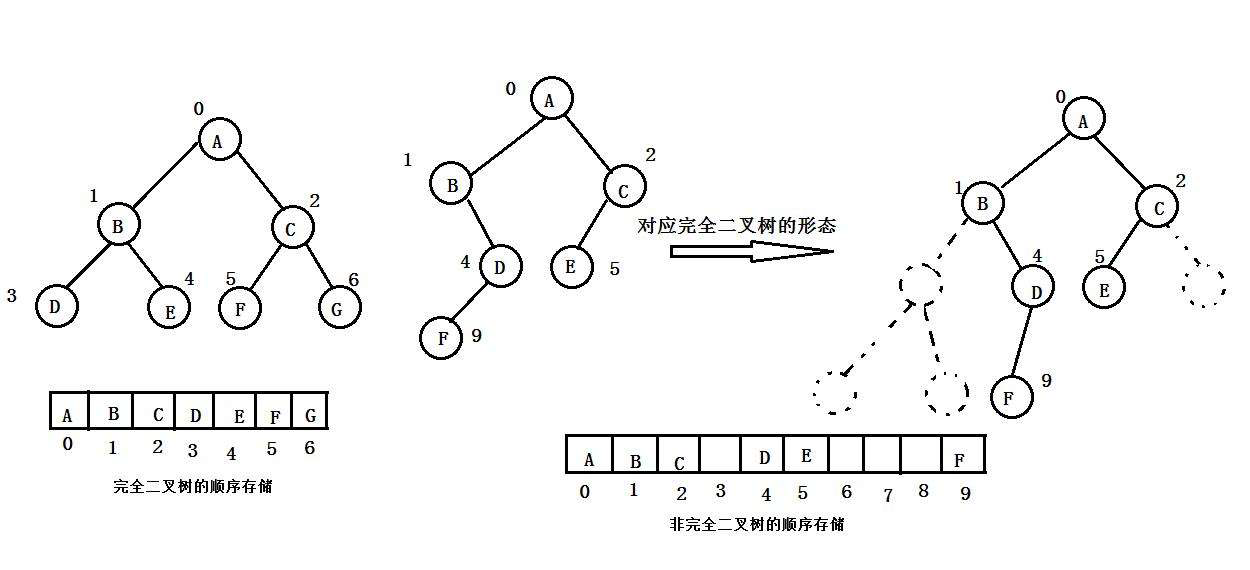
4 二叉树顺序存储
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
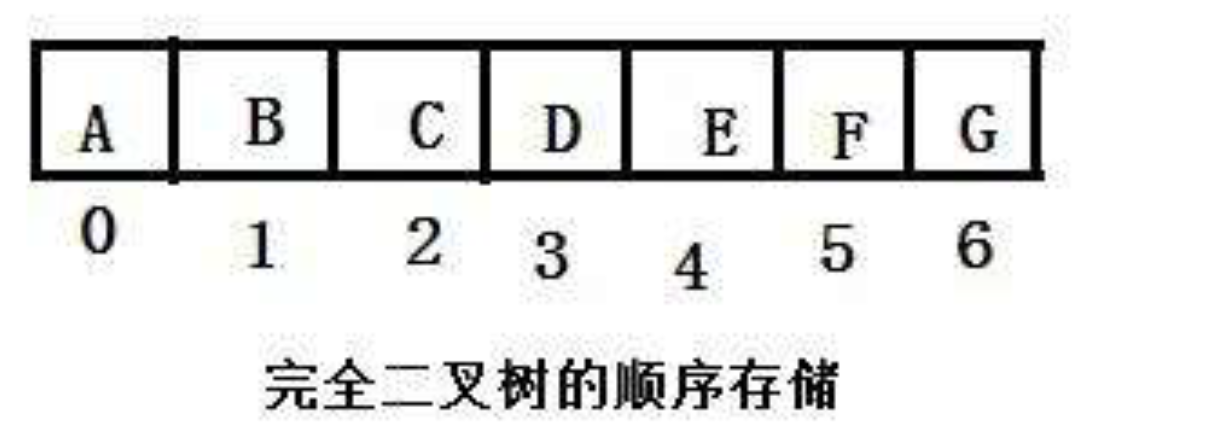
1.顺序结构存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆后面的章节会分析。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
注意:非完全二叉树可以用顺序存储,但是不太适合,因为会存在好多的空间浪费。
2.逻辑结构
想象出来的。
eg:
3.物理结构
内存中实实在在的存储的。
eg:
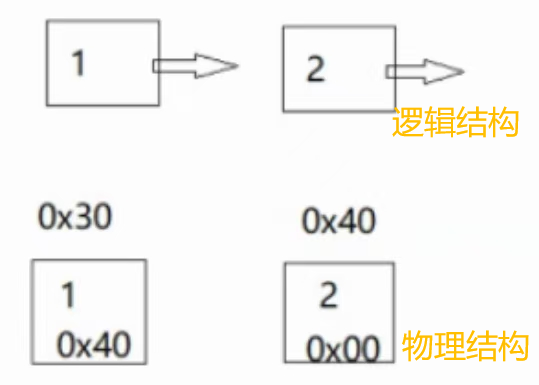
4.意义
用下标可以推导父子关系:
假设父亲在数组中的下标:i
则左孩子的下标为:2*i+1
右孩子的下标为:2*i+2
左孩子都是奇数,右孩子都是偶数。
假设知道孩子下标: j
则父亲下标:(j-1)/ 2 取整