力扣131:分割回文串
力扣131:分割回文串
- 题目
- 思路
- 代码
题目
给你一个字符串 s,请你将 s 分割成一些 子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
思路
从题目中我们可以总结出这道题的三个需要解决的问题:
- 如何判断回文串
- 如何找到一种方案里的所有回文子串
- 如何找到所有可能的分割方案
解决了这三个问题我们就解决了这道题,我们先从最简单的判断回文串开始,想要判断回文串我们只需要知道这个子串的开头位置和结尾位置然后判断字符串中两者所代表的值是否相同再将开头位置进行++结尾位置进行–来完成一个循环判断即可。直到开头位置大于等于结尾位置。
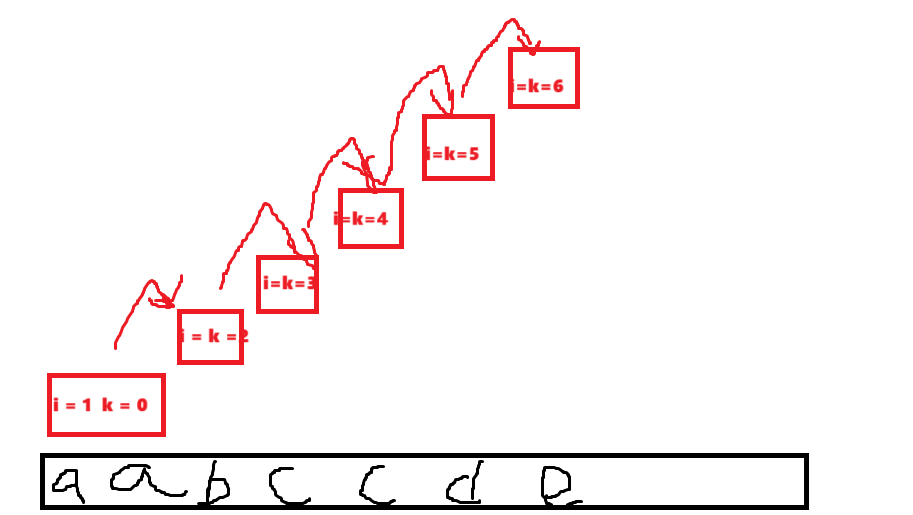
第一个问题解决了接下来我们来解决第二个问题,这里我们可以设计一个函数它的参数有两个分别是当前位置的下标i和开头位置的下标k,我们让当前位置i不等于字符串的结尾位置之前都调用自身但是当前位置要+1只有在当前位置等于字符串的结尾位置时才开始判断开头位置k和当前位置i这一个子串是否是字符串如果是就插入到一个数组中如果不是就直接返回到上一个位置因为是上一个位置调用了函数才导致当前位置到结尾位置的。然后就是上一个位置进行判断是否是回文串以此倒推直到找到回文串,之后呢我们再调用函数但是两个参数都要变成i+1也就是把当前位置和开头位置全部移到这个回文子串的下一个字符再进行判断。我可以用一个图来表示。

这样我们就可以得到一个数组里面存着每一个回文子串。
接下来就是第三个问题如何找到所有方案,这里我们可以使用回溯的方法,有些同学在我们是调用自身来进行分割子串时就发现了这其实是典型的回溯的办法,所以我们只需要在最后找到回文子串并且将其加入到数组中后再把这个回文子串进行pop掉就可以了。因为我们在i=n-1也就结尾位置后会和上图一样一层一层的调用自身直到i=n也就会存储已经有着一种方案的回文子串数组了之后我们再一层一层的把插入的回文子串给pop掉这样就可以继续得到下一种方案了。
代码
class Solution {
public:bool IsPalindrome(string& s , int left,int right){while(left < right){if(s[left++] != s[right--]){return false;}}return true;}vector<vector<string>> partition(string s) {int n = s.size();vector<vector<string>> res;vector<string> path;auto dfs = [&](this auto&& dfs,int i,int start){//当i=n时也就是一种方案的所有的回文串已经找完了if(i == n){res.emplace_back(path);return;}//一直到i = n-1也就是最后一个数if(i < n-1){dfs(i+1,start);}//从i处找到它的回文串if(IsPalindrome(s,start,i) == true){path.emplace_back(s.substr(start,i-start+1));//查找下一个位置的回文串dfs(i+1,i+1);//开始回溯path.pop_back();}};dfs(0,0);return res;}
};
