CART算法-理论部分
CART算法
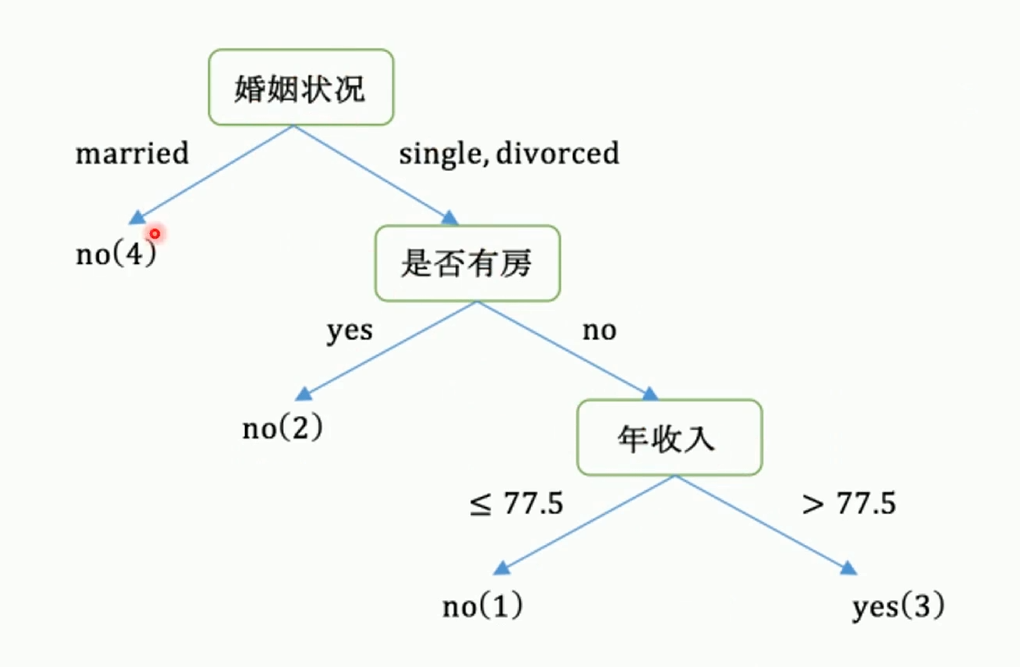
CART分类树
待预测结果是离散数据
CART分类树的生成是递归地构建二叉树的过程。使用基尼系数最小化准则进行特征选择
选择基尼指数最小:
使Gini(D,X)=∑i=1k∣Di∣∣D∣Gini(Di)最小那么基尼增益Gini(D)−Gini(D,X)就最大
使Gini(D,X)=\sum_{i=1}^{k}\frac{|D_i|}{|D|}Gini(D_i)最小\\
那么基尼增益Gini(D)-Gini(D,X)就最大
使Gini(D,X)=i=1∑k∣D∣∣Di∣Gini(Di)最小那么基尼增益Gini(D)−Gini(D,X)就最大
步骤
- 计算当前特征的基尼增益
- 选择基尼增益最大的特征作为划分特征
- 在该特征中查找基尼指数最小的分类类别作为最优划分点
- 将当前样本划分成两类,一类是划分特征的类别等于最优划分点,另一类是不等于
CART回归树
待预测结果是连续数据
CART 回归树通过递归划分数据空间,将整个特征空间划分为若干个子区域,每个子区域对应一个叶子节点。每个叶子节点的预测值是该区域内目标变量的均值
假设将输入空间划分为M个单元R1,R2,…,RM,并在每个单元RM上有一个固定输出值cm,回归树模型可表示为f(x)=∑m=1McmI(x∈Rm)I(x∈Rm)为适应函数,当x∈Rm时返回1,否则返回0(one−hot编码)
假设将输入空间划分为M个单元R_1,R_2,\dots,R_M,\\并在每个单元R_M上有一个固定输出值c_m,回归树模型可表示为\\
f(x)=\sum_{m=1}^{M}c_mI(x \in R_m) \\
I(x \in R_m)为适应函数,当x \in R_m时返回1,否则返回0(one-hot编码)
假设将输入空间划分为M个单元R1,R2,…,RM,并在每个单元RM上有一个固定输出值cm,回归树模型可表示为f(x)=m=1∑McmI(x∈Rm)I(x∈Rm)为适应函数,当x∈Rm时返回1,否则返回0(one−hot编码)
输入空间不断进行二分,最终分出M个叶子节点R_M,每个叶子节点选出一个代表值c_m作为输出
根据平方误差进行划分
平方误差:∑xi∈Rm(yi−f(xi))2
平方误差:\\
\sum_{x_i \in R_m}(y_i-f(x_i))^2
平方误差:xi∈Rm∑(yi−f(xi))2
最优输出选取:Rm上所有样本点y_i的平均值
cm^=average(yi∣xi∈Rm)
\hat{c_m} = average(y_i|x_i \in R_m)
cm^=average(yi∣xi∈Rm)
划分
选择第x(j)个变量和取值s(固定变量x(j)),分别作为切分变量和切分点,并定义两个区域:R1(j,s)={x∣x(j)≤s},R2(j,s)={x∣x(j)>s} 选择第x^{(j)}个变量和取值s(固定变量x^{(j)}),分别作为切分变量和切分点,并定义两个区域:\\ R_1(j,s) = \{x|x^{(j)}\leq s\},R_2(j,s)=\{x|x^{(j)} > s\} 选择第x(j)个变量和取值s(固定变量x(j)),分别作为切分变量和切分点,并定义两个区域:R1(j,s)={x∣x(j)≤s},R2(j,s)={x∣x(j)>s}
寻找最优切分变量j和最优切分点s
- 通过寻找不同切分点之间的最小平方误差找到x(j)中的最优切分点s
- 找到最优切分点s后,对于每个变量j,固定s,比较平方误差,找到最小平方误差,就找到了最优切分变量j
R1对应输出值为c1,R2对应输出值为c2
c1,c2对应R1,R2上所有样本点y_i的平均值
minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2]
\min_{j,s} [\min_{c_1}\sum_{x_i \in R_1(j,s)}(y_i-c_1)^2+\min_{c_2}\sum_{x_i \in R_2(j,s)}(y_i-c_2)^2]
j,smin[c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2]
对于固定输入变量j,可以找到最优切分点s,此时的最优输出c为
c1^=avg(yi∣xi∈R1(j,s))c2^=avg(yi∣xi∈R2(j,s))
\hat{c_1} = avg(y_i|x_i \in R_1(j,s)) \\
\hat{c_2} = avg(y_i|x_i \in R_2(j,s))
c1^=avg(yi∣xi∈R1(j,s))c2^=avg(yi∣xi∈R2(j,s))
例子
水果:甜(00.5)与好吃(010)的对应
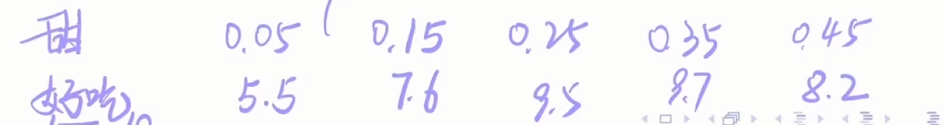
对特征-甜度进行划分,选取划分值s=(0.05+0.15)/2=0.1
R1={0.05},R2={0.15,0.25,0.35,0.45}c1^=5.5,c2^=(7.6+9.5+9.7+8.2)/4=8.75平方误差=0+(7.6−8.75)2+(9.5−8.75)2+(8.7−8.75)2+(8.2−8.75)2=3.09
R_1=\{0.05\},R_2=\{0.15,0.25,0.35,0.45\} \\
\hat{c_1} = 5.5,\hat{c_2} = (7.6+9.5+9.7+8.2)/4=8.75\\
平方误差=0+(7.6-8.75)^2+(9.5-8.75)^2+(8.7-8.75)^2+(8.2-8.75)^2=3.09
R1={0.05},R2={0.15,0.25,0.35,0.45}c1^=5.5,c2^=(7.6+9.5+9.7+8.2)/4=8.75平方误差=0+(7.6−8.75)2+(9.5−8.75)2+(8.7−8.75)2+(8.2−8.75)2=3.09
同理对s=0.2,0.3,0.4进行同样的计算

剪枝
使用代价复杂度损失函数
Cα(T)=C(T)+α∣T∣其中:T是任意子树C(T)为对训练数据的预测误差(基尼指数,平方误差等)∣T∣是T的叶子节点树α表示偏好系数,类似于正则化参数λ,越大表示对划分叶子节点惩罚越重
C_{\alpha}(T)=C(T)+\alpha|T| \\
其中:\\T是任意子树\\C(T)为对训练数据的预测误差(基尼指数,平方误差等)\\|T|是T的叶子节点树\\\alpha表示偏好系数,类似于正则化参数λ,越大表示对划分叶子节点惩罚越重
Cα(T)=C(T)+α∣T∣其中:T是任意子树C(T)为对训练数据的预测误差(基尼指数,平方误差等)∣T∣是T的叶子节点树α表示偏好系数,类似于正则化参数λ,越大表示对划分叶子节点惩罚越重
- α->0:对划分叶子节点无约束,最终的树拟合效果最好
- α->+∞:对划分叶子节点惩罚非常重,根节点组成的单节点树效果最优
对α的取值范围进行划分
0=a0<a1<a2<⋯<an<+∞每个α∈[αi,αi+1)都对应一颗完整决策树剪枝得到的子树序列对应着区间α∈[αi,αi+1)的最优子树序列{T0,T1,…,Tn}T0对应未剪枝的整棵树,Tn对应根节点
0= a_0<a_1<a_2<\dots<a_n<+∞\\
每个\alpha \in [\alpha_i,\alpha_{i+1})都对应一颗完整决策树\\
剪枝得到的子树序列对应着区间\alpha \in [\alpha_i,\alpha_{i+1})的最优子树序列\{T_0,T_1,\dots,T_n\}\\
T_0对应未剪枝的整棵树,T_n对应根节点
0=a0<a1<a2<⋯<an<+∞每个α∈[αi,αi+1)都对应一颗完整决策树剪枝得到的子树序列对应着区间α∈[αi,αi+1)的最优子树序列{T0,T1,…,Tn}T0对应未剪枝的整棵树,Tn对应根节点
这个子树序列是嵌套的:
T0是T1的子树,T2是T1的子树,直到根节点Tn
对剪枝前后损失函数进行比较
-
剪枝前
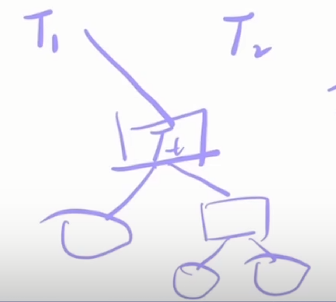
Cα(Tt)=C(Tt)+α∣Tt∣C_{\alpha}(T_t) = C(T_t)+\alpha|T_t|Cα(Tt)=C(Tt)+α∣Tt∣ -
剪枝后
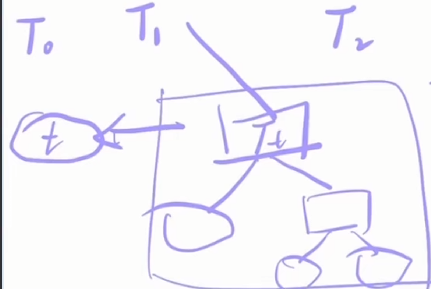
整个子树Tt变成内部节点tCα(t)=C(t)+α单节点,所以∣t∣=1整个子树T_t变成内部节点t\\C_{\alpha}(t)=C(t)+\alpha\\单节点,所以|t|=1整个子树Tt变成内部节点tCα(t)=C(t)+α单节点,所以∣t∣=1-
α->0时,追求拟合效果,那么当然是不剪枝的代价更小,即
Cα(Tt)<Cα(t)C_{\alpha}(T_t) < C_{\alpha}(t)Cα(Tt)<Cα(t) -
α增大到一定程度时,剪枝与不剪枝的代价相同,即
Cα(Tt)=Cα(t)从这个式子就可以推出α=C(t)−C(Tt)∣Tt∣−1C_{\alpha}(T_t) = C_{\alpha}(t) \\从这个式子就可以推出\alpha = \frac{C(t)-C(T_t)}{|T_t|-1}Cα(Tt)=Cα(t)从这个式子就可以推出α=∣Tt∣−1C(t)−C(Tt) -
α->+∞时,剪枝的代价更小,即
Cα(Tt)>Cα(t)C_{\alpha}(T_t) > C_{\alpha}(t)Cα(Tt)>Cα(t)
-
算法步骤

第(3)的:g(t)=C(t)−C(Tt)∣Tt∣−1,α=min(α,g(t))是为了选出所有节点中拥有最小g(t)的节点T
第(3)的:
g(t) =\frac{C(t)-C(T_t)}{|T_t|-1},\alpha=min(\alpha,g(t))是为了选出所有节点中拥有最小g(t)的节点T
第(3)的:g(t)=∣Tt∣−1C(t)−C(Tt),α=min(α,g(t))是为了选出所有节点中拥有最小g(t)的节点T
得到α和T,就递归调用(3)-(5)步,最终得到T1,T2,…,Tn,使用交叉验证得到最优子树
