【机器学习-1】特征工程与KNN分类算法
0 序言
在机器学习的知识体系里,特征工程是模型构建的基石,它决定了数据的质量。
而 KNN,也叫K近邻算法作为经典的分类算法,简单直观又实用。
这两者对理解和实践机器学习都至关重要,本篇文章就围绕这两方面的内容进行介绍。
1 特征工程
1.1 是什么
特征工程是将原始数据转化为更能代表模型潜在问题特征的过程,目的是提升对未知数据预测的准确性 。打个比方,就像AlphaGo学习时,数据里既有棋谱之类有效信息,又有错误落子之类噪声,若不处理,会干扰学习效果,特征工程就是清理并优化这些数据,让模型学明白。
1.2 为什么需要
样本数据里的特征常存在缺失值、重复值、异常值等“瑕疵”。
处理这些,一方面是为了得到更干净的样本集,另一方面能让模型基于优质数据,发挥出更好的预测能力,不是单纯为处理而处理,是服务于模型效果提升 。
1.3 包含哪些环节
- 特征抽取:从原始数据里挖掘、提炼出
有价值的特征,比如从文本描述里提取关键词作为特征 。 - 数据特征的预处理:对抽取的特征做
打磨,比如常见类型有填充缺失值、处理异常值、归一化等,让特征更规整 。 - 特征选择:从众多特征里筛选出最关键、最有代表性的,
避免冗余特征干扰模型,提升效率与效果 。
2 KNN 分类算法(K-Nearest Neighbors, KNN)
2.1 核心原理
KNN 算法是基于物以类聚思想的分类算法。
它的核心逻辑是:要判断一个样本的类别,就看它周围,或者说设定范围内最近的K个邻居样本的类别,通过少数服从多数原则,确定该样本类别。
2.2 欧氏距离(常用距离度量方式)
在 KNN 里,计算样本间距离是确定邻居的关键,欧氏距离是常用方法。
对于两个 n 维样本点,下面用A,B来表示。
A(x11,x12,...,x1n) A(x_{11},x_{12},...,x_{1n}) \ A(x11,x12,...,x1n)
和
B(x21,x22,...,x2n) B(x_{21},x_{22},...,x_{2n}) B(x21,x22,...,x2n)
那么,
欧氏距离公式为:
d(A,B)=∑i=1n(x1i−x2i)2 d(A,B)=\sqrt{\sum_{i = 1}^{n}(x_{1i}-x_{2i})^2} d(A,B)=i=1∑n(x1i−x2i)2
简单说,就是把每个维度上的坐标差平方后相加,再开平方,得到的数值越小,代表两个样本越近
3 算法示例理解
我这边做了一些图示,来帮助读者更好地理解它的原理。
看KNN图示,不同形状、颜色代表不同类别样本
这里,我用两种类别样本:
一类是蓝色的圆形,另一类则是绿色的三角形,
用这两个图形来表示两类。
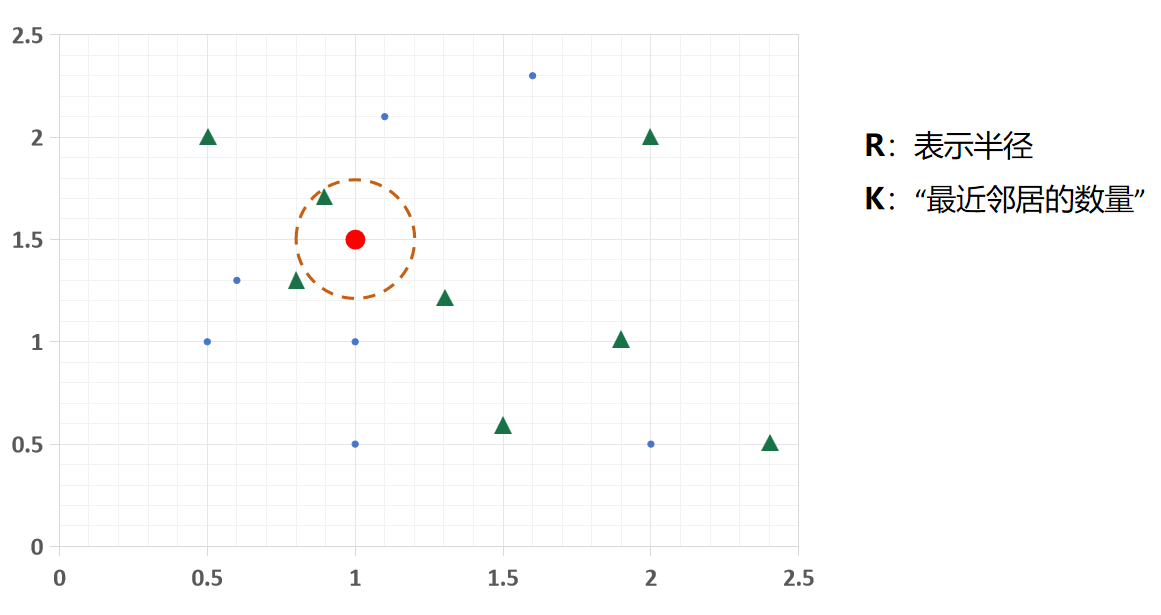
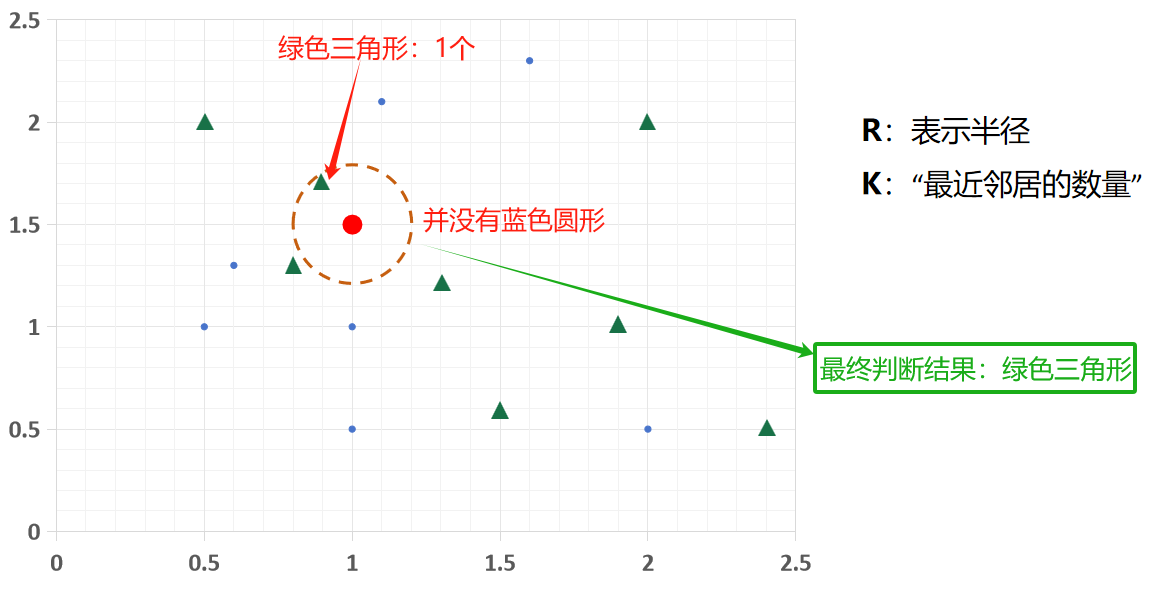
当R = 0.3,K = 1时,看待分类样本(paw标记)最近的 1 个邻居,邻居是三角形,所以它被分为三角形类别;
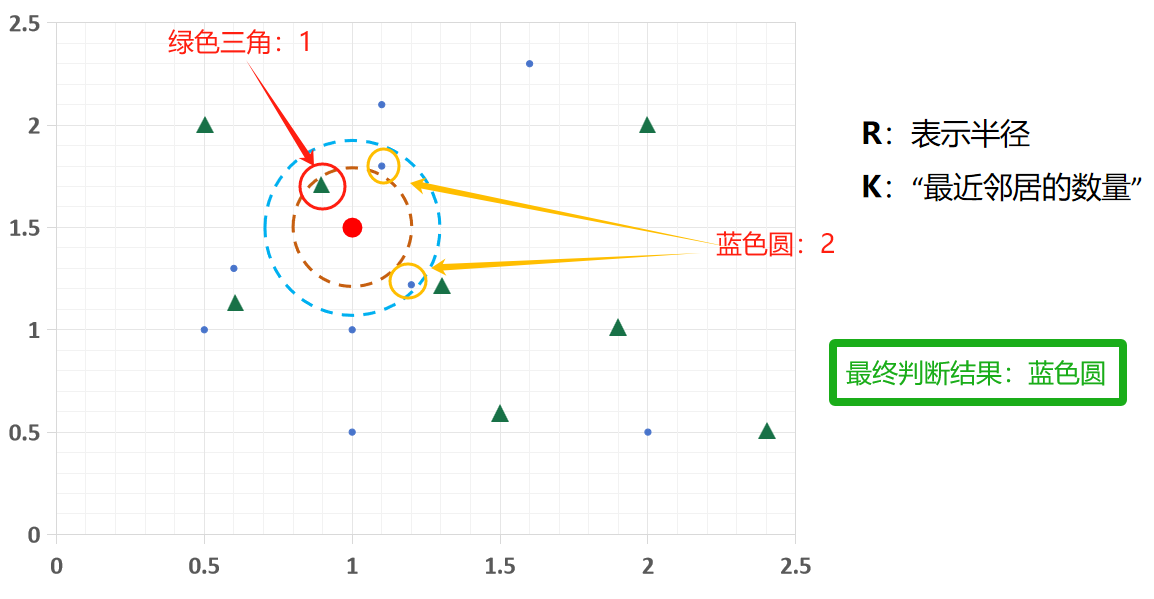
当R=0.42,k = 3时,找最近 3 个邻居,圆形有 2 个、三角形 1 个,多数决定它是圆形;
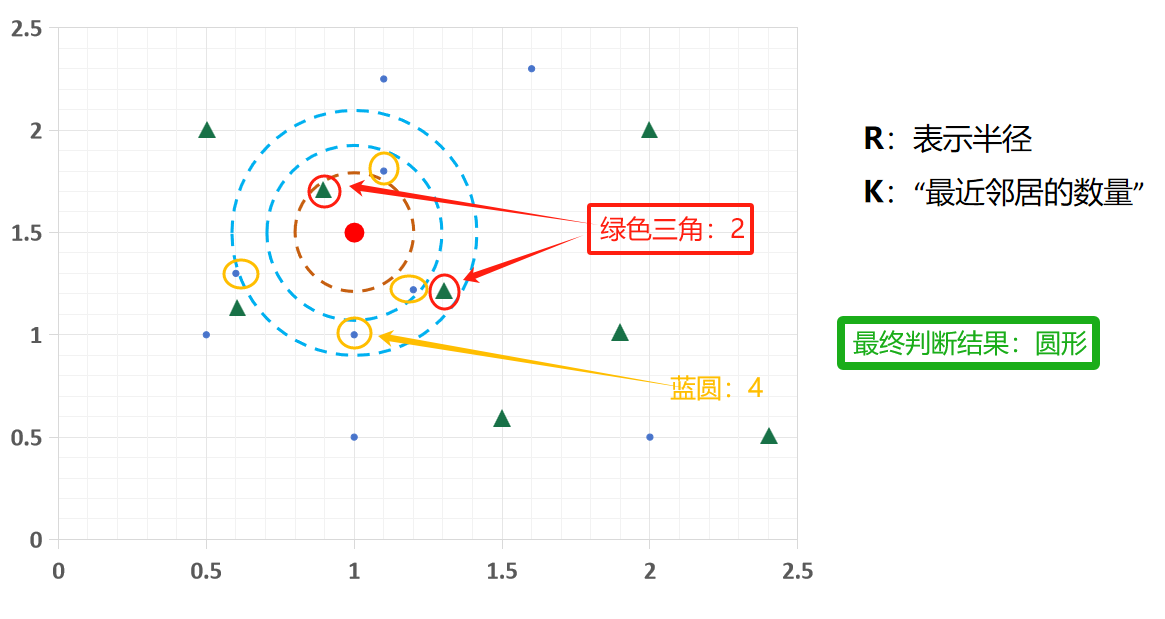
同理,
当R = 0.6,k = 6时,最近 6 个邻居里三角形占 2 个、圆形 4 个,就被分为圆形类别 。
这体现了 K 值不同,分类结果可能变化,选合适K值很重要!!!
K 太小(如 K=1 ):模型容易受单个样本噪声影响。
若最近邻居是异常点,预测结果会出错,相当于模型过拟合,
过度依赖局部单个样本,忽略整体规律 。
K 太大(如 K 接近数据集样本总数 ):模型会忽略局部特征,趋向平均,
不同类别样本易被混在一起,导致欠拟合,预测准确性下降 。
换句话说,如果说你得K取值无限趋近于全部数,
那此时KNN的判断方式以多数服从少数来说,
那不就是把两种类别全都混杂一块,然后多的就输出出来,
那不就是平均化了嘛。
3 小结
本文聚焦知识原理梳理,先把特征工程和 KNN的核心逻辑讲清楚,构建知识框架,
后续再通过实战拓展作为延伸,由浅入深 。
