当前位置：首页 > news >正文

【线段树】P8473 [Aya Round 1 H] 破碎的历史|普及+

news 2025/7/27 6:06:16

本文涉及知识点

C++线段树

[Aya Round 1 H] 破碎的历史

题目背景

幻想乡迎来了它的毁灭，幻想的载体也已经遁入了幻想。

所幸的是，幻想乡中的乡民们还侥幸存活着，她们在尝试恢复幻想乡的历史。然而历史之中的大大小小的事情不计其数，人们只能记得起一些大事情罢了。

或许，根据那些重要的事情，可以把次要的事件推导出来呢？

题目描述

数轴的正半轴上有 $n$ 个互不相同的被黑白染色的特殊整点，位置从左到右依次为 $p1,p2,⋯,pnp_1,p_2,\cdots,p_n$ 。维护初始为空的可重线段集合 $S$ 。

$q$ 次操作。操作分若干种，具体格式如下：

1 l r：将所有满足 $\le x \le y \le r$ 且两端点均为特殊整点的线段 $[x, y]$ 加入 $S$ 。
2 x：撤回第 $x$ 次操作添加的线段。

在初始时和每次操作后，假设你可以进行任意次（可以是零次）染色。每次从 $S$ 中选出一条线段 $[x, y]$ ，满足位于点 $x$ 和点 $y$ 的特殊整点均为黑色，然后将所有在线段内的白色特殊整点染黑。试判断是否存在至少一种合法染色方式使得正半轴上的所有特殊整点均被染黑（即，不存在白色特殊整点）。注意：所有的询问均为「假设」，即各组询问之间独立，不会造成对数轴的实际修改。

输入格式

第一行输入两个整数 $n, q$ 。
第二行输入 $n$ 个整数 $p1,p2,⋯,pnp_1,p_2,\cdots,p_n$ ，表示 $n$ 个特殊整点从左到右的位置。
第三行输入 $n$ 个整数 $a1,a2,⋯,ana_1,a_2,\cdots,a_n$ ，表示特殊整点的颜色。其中 $a_i=0$ 表示白色， $a_i=1$ 表示黑色。
接下来 $q$ 行，每行二至三个整数，表示一次操作。

输出格式

输出共 $(q + 1)$ 行。
在初始时和每次操作后，输出一行一个字符串：
- yes 代表存在合法染色方式。
- no 代表不存在合法染色方式。
你可以输出字符串的任意大小写形式。例如：字符串 yes、Yes、YES 均会被视为表示存在合法染色方式。

样例 #1

样例输入 #1

6 3
1 2 3 5 8 13
1 0 0 1 0 1
1 5 10
1 1 15
2 2

样例输出 #1

No
No
Yes
No

提示

样例解释

六个特殊点的位置/颜色在数轴正半轴上如图所示。

容易发现，并非所有点都是黑点。因此在进行操作前，输出 $NO\verb!NO!$ 。

第一次操作后，一共往 $S$ 加入了三条线段： $[5, 5], [8, 8], [5, 8]$ （图中省略了端点重叠的线段）。容易发现，此时无法进行任何操作，因此没法将所有点变成黑点。输出 $NO\verb!NO!$ 。

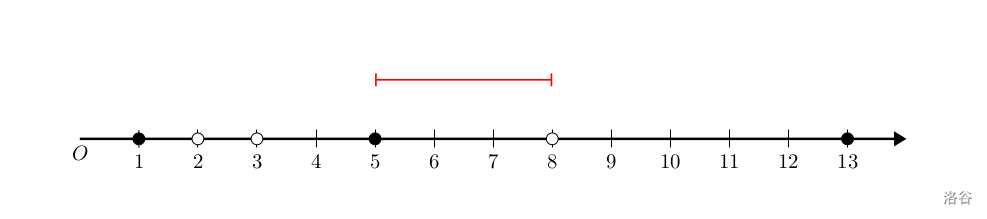
第二次操作后，又往 $S$ 中加入了 $20$ 条线段。除去端点重叠的选段，在 $S$ 中如图所示。（以示区别，上一次操作加入的边标成了深蓝色）。

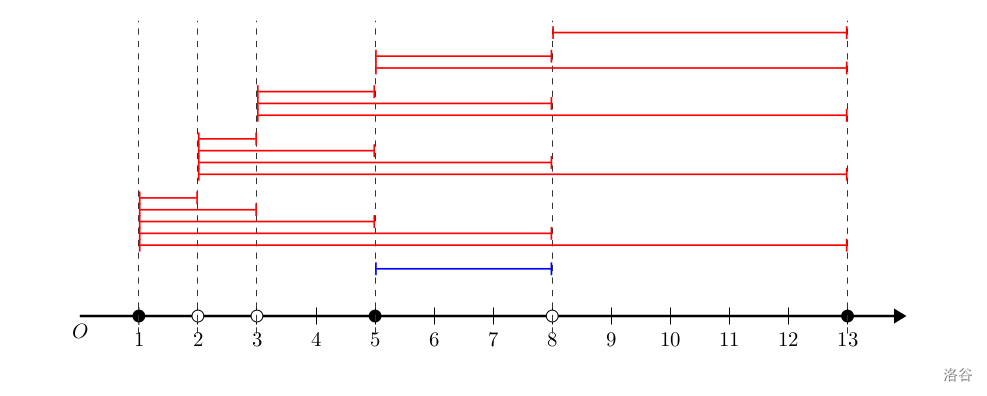
可以找出一种方案，将图上所有特殊点变成黑点。具体而言，首先选择 $S$ 中 $[1, 5]$ 线段（容易发现位于 $1$ 和 $5$ 的特殊点均为黑点，因此可以进行染色），那么可以把位于 $2$ 和 $3$ 的点染色。

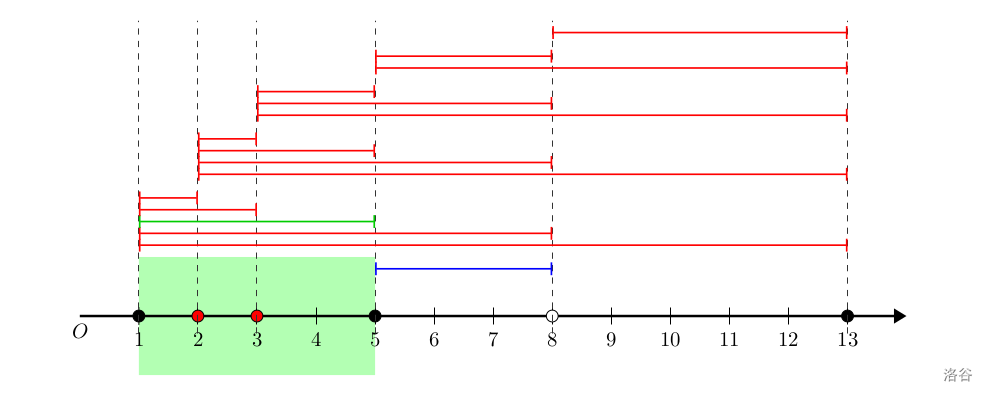
此时又可以选择 $S$ 中 $[3, 13]$ 线段（在上一轮操作中， $3$ 号点变为了黑点，因此 $[3, 13]$ 符合条件），将点 $8$ 染为黑色。

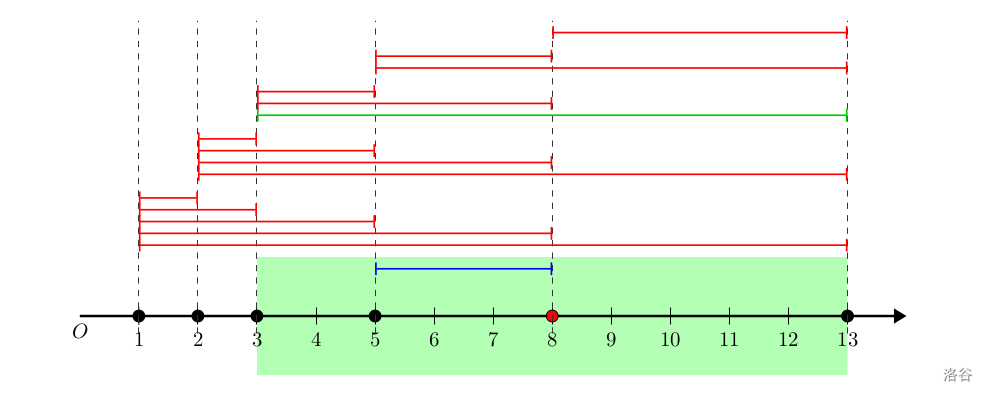
此时所有点都为黑色，因此输出 $YES\verb!YES!$ 。再次强调，询问之间互相独立，且只是询问是否存在染色方案，而不会对特殊整点进行实际上的染色操作。

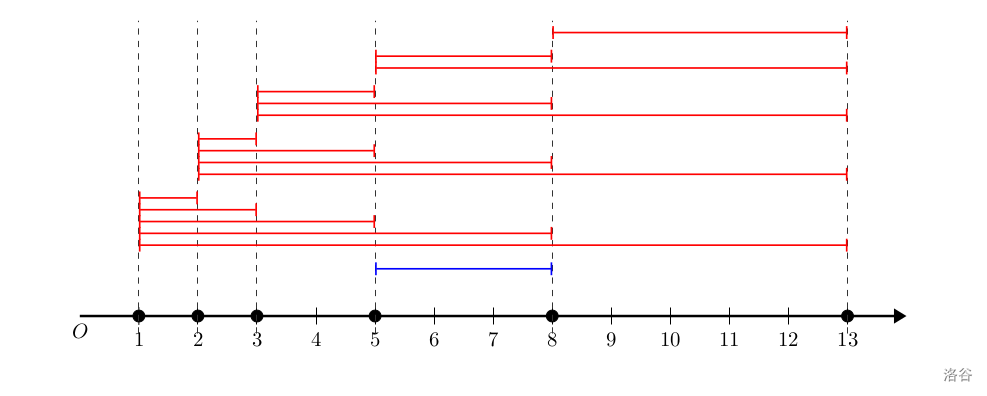
第三个操作撤回了第二个操作往 $S$ 里加入的所有线段。因此退回到了只有第一个操作的情况。不存在一种方案将所有点染黑，因此输出 $NO\verb!NO!$ 。

数据范围

对于所有数据， $\le n,q \le 5 \times 10^5$ ， $ai∈{0,1}a_i \in \{0,1\}$ ， $\le l< r \le 10^9$ ， $\le p_i \le 10^9$ 。保证 $p_i$ 单调递增， $2$ 操作撤销的只会是 $1$ 操作，且每个操作最多被撤销一次。

线段树

每次操作只需要增加、撤销最大黑色区间。
如果存在区间[left,r]，则这个区间所有的点都可以变成黑点。
增加区间[left,r]，则[left,r]++。
初始为黑点，则最[x]++。
初始状态或操作后，返回整个区间是否都大于0。
数据结构用最小值线段树

代码

核心代码

#include <iostream>
#include <sstream>
#include <vector>
#include<map>
#include<unordered_map>
#include<set>
#include<unordered_set>
#include<string>
#include<algorithm>
#include<functional>
#include<queue>
#include <stack>
#include<iomanip>
#include<numeric>
#include <math.h>
#include <climits>
#include<assert.h>
#include<cstring>
#include<list>#include <bitset>
using namespace std;template<class T1, class T2>
std::istream& operator >> (std::istream& in, pair<T1, T2>& pr) {in >> pr.first >> pr.second;return in;
}template<class T1, class T2, class T3 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3>& t) {in >> get<0>(t) >> get<1>(t) >> get<2>(t) ;return in;
}template<class T1, class T2, class T3, class T4 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3, T4>& t) {in >> get<0>(t) >> get<1>(t) >> get<2>(t) >> get<3>(t);return in;
}template<class T = int>
vector<T> Read() {int n;scanf("%d", &n);vector<T> ret(n);for(int i=0;i < n ;i++) {cin >> ret[i];}return ret;
}template<class T = int>
vector<T> Read(int n) {vector<T> ret(n);for (int i = 0; i < n; i++) {cin >> ret[i];}return ret;
}template<int N = 12 * 1'000'000>
class COutBuff
{
public:COutBuff() {m_p = puffer;}inline void write(int x) {int num[12], sp = 0;if (x < 0)*m_p++ = '-', x = -x;if (!x)*m_p++ = 48;while (x)num[++sp] = x % 10, x /= 10;while (sp)*m_p++ = num[sp--] + 48;}inline void write(char ch){*m_p++ = ch;}inline void ToFile() {fwrite(puffer, 1, m_p - puffer, stdout);}
private:char  puffer[N], * m_p;
};template<int N = 12 * 1'000'000>
class CInBuff
{
public:inline CInBuff() {fread(buffer, 1, N, stdin);}inline int Read() {int x(0), f(0);while (!isdigit(*S))f |= (*S++ == '-');while (isdigit(*S))x = (x << 1) + (x << 3) + (*S++ ^ 48);return f ? -x : x;}
private:char buffer[N], * S = buffer;
};template<class TSave, class TRecord >
class CRangUpdateLineTree
{
protected:virtual void OnQuery(const TSave& save, const int& iSaveLeft, const int& iSaveRight) = 0;virtual void OnUpdate(TSave& save, const int& iSaveLeft, const int& iSaveRight, const TRecord& update) = 0;virtual void OnUpdateParent(TSave& par, const TSave& left, const TSave& r, const int& iSaveLeft, const int& iSaveRight) = 0;virtual void OnUpdateRecord(TRecord& old, const TRecord& newRecord) = 0;
};template<class TSave, class TRecord >
class CVectorRangeUpdateLineTree : public CRangUpdateLineTree<TSave, TRecord>
{
public:CVectorRangeUpdateLineTree(int iEleSize, TSave tDefault, TRecord tRecordNull) :m_iEleSize(iEleSize), m_save(iEleSize * 4, tDefault), m_record(iEleSize * 4, tRecordNull) {m_recordNull = tRecordNull;}void Update(int iLeftIndex, int iRightIndex, TRecord value){Update(1, 0, m_iEleSize - 1, iLeftIndex, iRightIndex, value);}void Query(int leftIndex, int rightIndex) {Query(1, 0, m_iEleSize - 1, leftIndex, rightIndex);}//void Init() {//	Init(1, 0, m_iEleSize - 1);//}TSave QueryAll() {return m_save[1];}void swap(CVectorRangeUpdateLineTree<TSave, TRecord>& other) {m_save.swap(other.m_save);m_record.swap(other.m_record);std::swap(m_recordNull, other.m_recordNull);assert(m_iEleSize == other.m_iEleSize);}
protected://void Init(int iNodeNO, int iSaveLeft, int iSaveRight)//{//	if (iSaveLeft == iSaveRight) {//		this->OnInit(m_save[iNodeNO], iSaveLeft);//		return;//	}//	const int mid = iSaveLeft + (iSaveRight - iSaveLeft) / 2;//	Init(iNodeNO * 2, iSaveLeft, mid);//	Init(iNodeNO * 2 + 1, mid + 1, iSaveRight);//	this->OnUpdateParent(m_save[iNodeNO], m_save[iNodeNO * 2], m_save[iNodeNO * 2 + 1], iSaveLeft, iSaveRight);//}void Query(int iNodeNO, int iSaveLeft, int iSaveRight, int iQueryLeft, int iQueryRight) {if ((iSaveLeft >= iQueryLeft) && (iSaveRight <= iQueryRight)) {this->OnQuery(m_save[iNodeNO], iSaveLeft, iSaveRight);return;}if (iSaveLeft == iSaveRight) {//没有子节点return;}Fresh(iNodeNO, iSaveLeft, iSaveRight);const int mid = iSaveLeft + (iSaveRight - iSaveLeft) / 2;if (mid >= iQueryLeft) {Query(iNodeNO * 2, iSaveLeft, mid, iQueryLeft, iQueryRight);}if (mid + 1 <= iQueryRight) {Query(iNodeNO * 2 + 1, mid + 1, iSaveRight, iQueryLeft, iQueryRight);}}void Update(int iNode, int iSaveLeft, int iSaveRight, int iOpeLeft, int iOpeRight, TRecord value){if ((iOpeLeft <= iSaveLeft) && (iOpeRight >= iSaveRight)){this->OnUpdate(m_save[iNode], iSaveLeft, iSaveRight, value);this->OnUpdateRecord(m_record[iNode], value);return;}if (iSaveLeft == iSaveRight) {return;//没有子节点}Fresh(iNode, iSaveLeft, iSaveRight);const int iMid = iSaveLeft + (iSaveRight - iSaveLeft) / 2;if (iMid >= iOpeLeft){Update(iNode * 2, iSaveLeft, iMid, iOpeLeft, iOpeRight, value);}if (iMid + 1 <= iOpeRight){Update(iNode * 2 + 1, iMid + 1, iSaveRight, iOpeLeft, iOpeRight, value);}// 如果有后代，至少两个后代this->OnUpdateParent(m_save[iNode], m_save[iNode * 2], m_save[iNode * 2 + 1], iSaveLeft, iSaveRight);}void Fresh(int iNode, int iDataLeft, int iDataRight){if (m_recordNull == m_record[iNode]){return;}const int iMid = iDataLeft + (iDataRight - iDataLeft) / 2;Update(iNode * 2, iDataLeft, iMid, iDataLeft, iMid, m_record[iNode]);Update(iNode * 2 + 1, iMid + 1, iDataRight, iMid + 1, iDataRight, m_record[iNode]);m_record[iNode] = m_recordNull;}vector<TSave> m_save;vector<TRecord> m_record;TRecord m_recordNull;const int m_iEleSize;
};template<class TSave, class TRecord >
class  CAddMinLineTree : public CVectorRangeUpdateLineTree<TSave, TRecord>
{
public:TSave m_ans;CAddMinLineTree(int iEleSize, TSave tDefault, TRecord tRecordNull) :CVectorRangeUpdateLineTree<TSave, TRecord>(iEleSize, tDefault, tRecordNull){m_ans = tDefault;}
protected:virtual void OnQuery(const TSave& save, const int& iSaveLeft, const int& iSaveRight) {m_ans = min(m_ans, save);}virtual void OnUpdate(TSave& save, const int& iSaveLeft, const int& iSaveRight, const TRecord& update) override{save += update;}virtual void OnUpdateParent(TSave& par, const TSave& left, const TSave& r, const int& iSaveLeft, const int& iSaveRight)  override{par = min(left, r);}virtual void OnUpdateRecord(TRecord& old, const TRecord& newRecord) override{old += newRecord;}
};class Solution {
public:vector<bool> Ans(vector<int>& p, vector<int>& a, vector<pair<int, int>>& que) {const int N = a.size();CAddMinLineTree<int, int> minTree(N, 0, 0);map<int, int> mBlack;for (int i = 0; i < N; i++) {if (a[i] == 1) {minTree.Update(i, i, 1);mBlack[p[i]] = i;}}vector<pair<int, int>> record;vector<bool> ans = { minTree.QueryAll() > 0 };for (const auto& [left, r] : que) {if (-1 == r) {auto [l1, r1] = record[left - 1];if (-1 != l1){minTree.Update(l1, r1, -1);}record.emplace_back(-1, -1);}else {auto it1 = mBlack.lower_bound(left);auto it2 = mBlack.upper_bound(r);if (it1 == it2) {record.emplace_back(-1, -1);}else {--it2;record.emplace_back(it1->second, it2->second);minTree.Update(it1->second, it2->second, 1);}}ans.emplace_back(minTree.QueryAll() > 0);}return ans;}
};int main() {
#ifdef _DEBUGfreopen("a.in", "r", stdin);
#endif // DEBUG	int n,q;cin >> n >> q;auto p = Read<int>(n);auto a = Read<int>(n);vector<pair<int, int>> que(q);int tmp;for (int i = 0; i < q; i++) {cin >> tmp >> que[i].first;if (2 == tmp) {que[i].second = -1;}else {cin >> que[i].second;}}auto res = Solution().Ans(p, a, que);for (const auto& b : res) {cout << (b ? "yes" : "no")<<endl;}
#ifdef _DEBUG		/*printf("a0=%d", a0);*//*Out(p, "p=");Out(a, ",a=");Out(que, ",que=");*/
#endif // DEBUG		return 0;
}

单元测试

vector<int> p, a;vector<pair<int, int>> que;TEST_METHOD(TestMethod11){p = { 1,2,3,5,8,13 }, a = { 1,0,0,1,0,1 }, que = { {5,10},{1,15},{2,-1} };auto res = Solution().Ans(p,a,que);AssertEx({ false,false,true,false }, res);}

扩展阅读

我想对大家说的话
工作中遇到的问题，可以按类别查阅鄙人的算法文章，请点击《算法与数据汇总》。
学习算法：按章节学习《喜缺全书算法册》，大量的题目和测试用例，打包下载。重视操作
有效学习：明确的目标及时的反馈拉伸区（难度合适）专注
闻缺陷则喜(喜缺)是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛
失败+反思=成功成功+反思=成功