统计学07:概率论基础
一、基础概念
概率p代表事件发生的可能性大小,在0-1范围内
ab测试中的p值,就代表一种概率(在零假设成立的前提下,观察当前数据或者比当前数据更加极端的数据的概率,p值越小,意味着在零假设成立的情况下,观察到当前结果的概率越小)
二、基本性质
非负性:P(A)>=0
规范性:整个样本空间发生的概率是1
加法公式:两个事件A和B的概率之和是 P(A∪B)=P(A)+P(B)−P(A∩B)(非互斥事件)
P(A∪B)=P(A)+P(B)(互斥事件)
条件概率:在事件B发生的前提下,事件A发生的概率
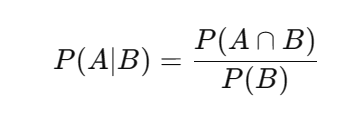
应用场景:当客户是高活跃客户的情况下,参加活动的概率;当客户历史参加过活动的情况下,再次参加活动的概率
全概率公式:
如果事件 B 可以分解为互斥的事件 B1,B2,…,Bn,则:
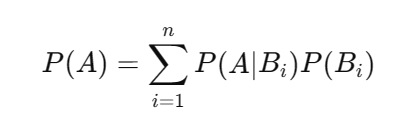
贝叶斯公式:
条件概率的逆向计算公式,帮助我们从已知结果推测原因:
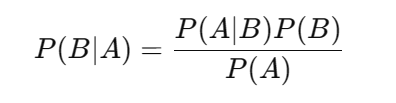
- P(A∣B):在事件 B 已发生的情况下,事件 A 的概率(后验概率)。
- P(A):事件 A 的初始概率(先验概率)。
- P(B∣A):在事件 A 发生的情况下,事件 B 的概率(似然)。
- P(B):事件 B 的总体概率。
实际场景下,可以因为用户的不同行为来调整他未来发生某事件的概率,从而动态的调整策略。
案例:一种疾病的发病率为 1%,测试的准确率为 95%,误报率为 5%。假如一个人测试呈阳性,他实际患病的概率是多少?
1)定义事件:A:患病 p(A)=0.01 B:阳性
2)已知条件:
- P(B|A)=0.95 P(B|~A)=0.05 P(~A)=0.99
3)计算P(B)=P(B∣A)P(A)+P(B∣非A)P(非A)=0.059
4)计算B发生前提下,A发生概率
P(A|B)=P(B|A)*P(A)/P(B) = 0.161
