算法第三十九天:动态规划part07(第九章)
1.打家劫舍
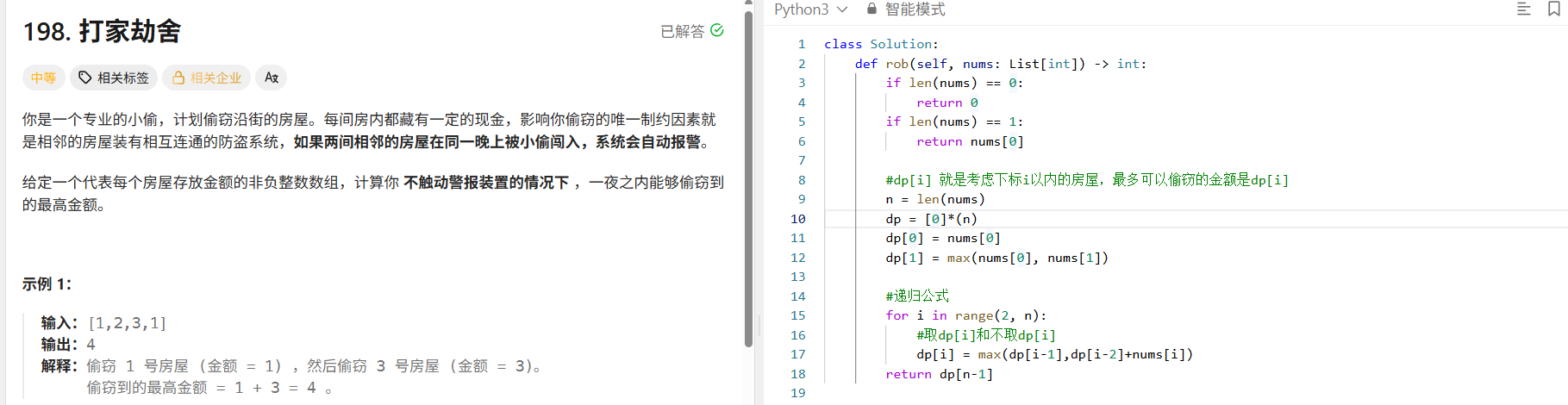
思路:动规五部曲

class Solution:def rob(self, nums: List[int]) -> int:if len(nums) == 0:return 0if len(nums) == 1:return nums[0]#dp[i] 就是考虑下标i以内的房屋,最多可以偷窃的金额是dp[i]n = len(nums)dp = [0]*(n)dp[0] = nums[0]dp[1] = max(nums[0], nums[1])#递归公式for i in range(2, n):#取dp[i]和不取dp[i]dp[i] = max(dp[i-1],dp[i-2]+nums[i])return dp[n-1]
2.打家劫舍II
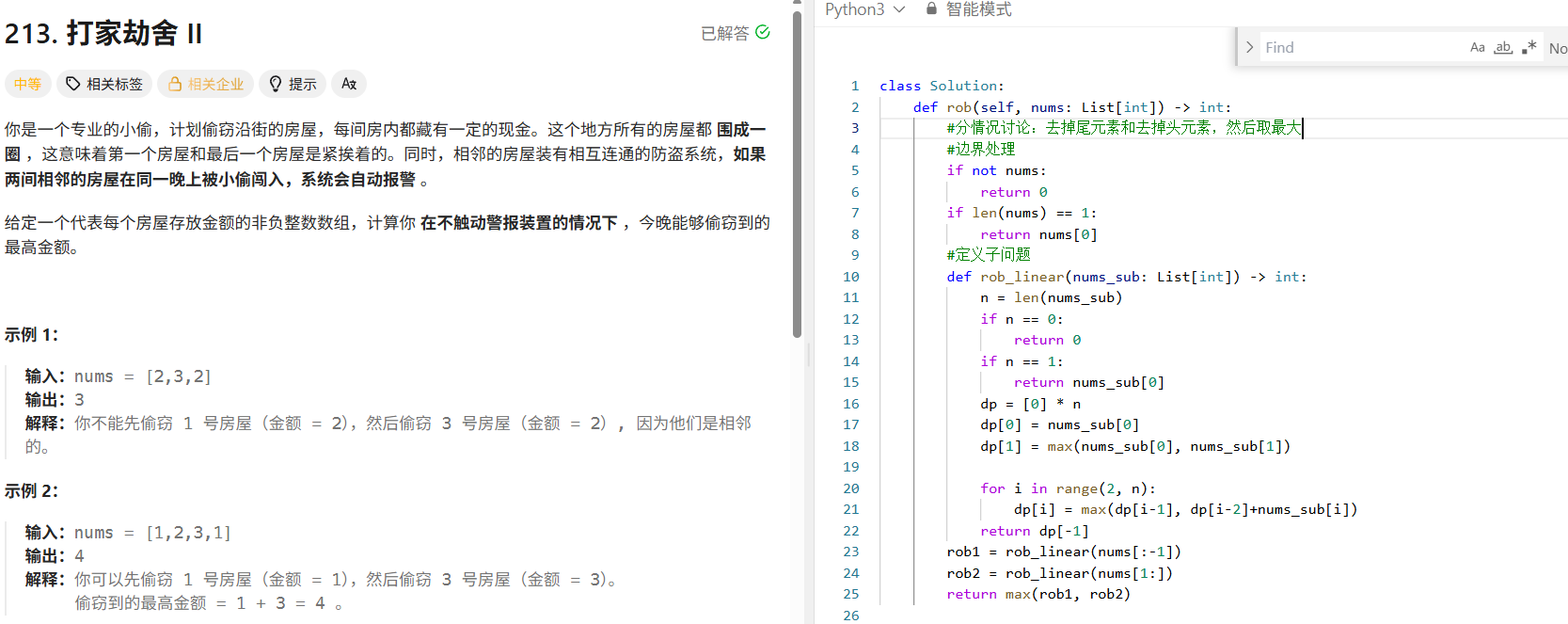
class Solution:def rob(self, nums: List[int]) -> int:#分情况讨论:去掉尾元素和去掉头元素,然后取最大#边界处理if not nums:return 0if len(nums) == 1:return nums[0]#定义子问题def rob_linear(nums_sub: List[int]) -> int: n = len(nums_sub)if n == 0:return 0if n == 1:return nums_sub[0]dp = [0] * n dp[0] = nums_sub[0]dp[1] = max(nums_sub[0], nums_sub[1])for i in range(2, n):dp[i] = max(dp[i-1], dp[i-2]+nums_sub[i])return dp[-1]rob1 = rob_linear(nums[:-1])rob2 = rob_linear(nums[1:])return max(rob1, rob2)3.打家劫舍Ⅲ
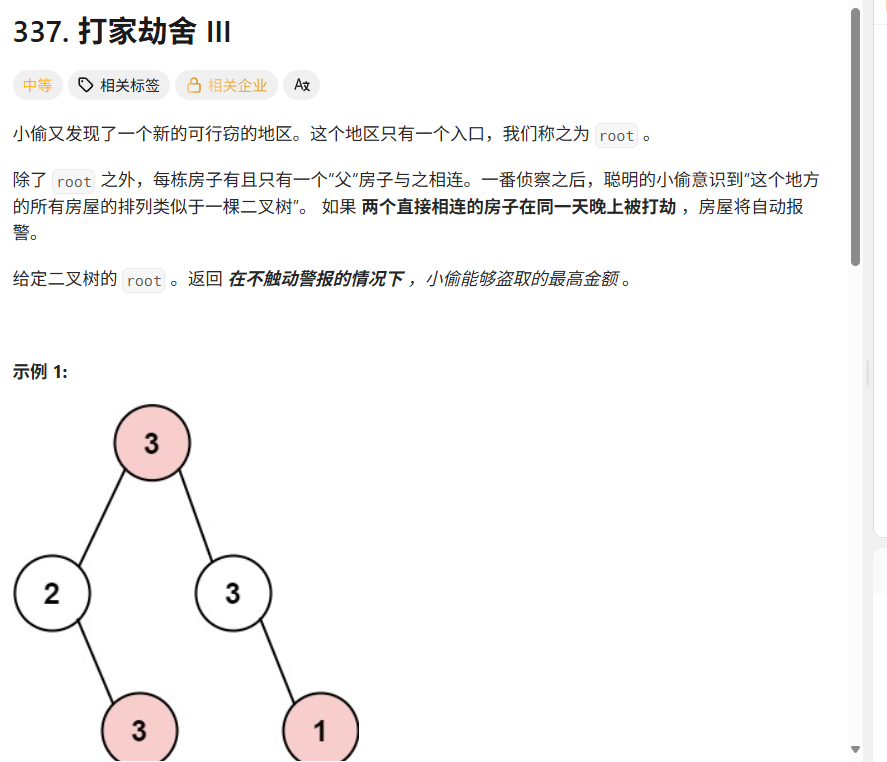
思路总结:
✅ 解题思路总结:
1. 递归目标:
函数 dfs(node) 计算并返回:
(不偷当前节点的最大收益, 偷当前节点的最大收益)
即一个二元组,代表该节点为根的子树两种状态下的最大收益。
2. 为什么要递归调用左右子节点?
当前节点偷不偷,依赖于左右子节点偷与不偷的收益。
递归调用左右子节点:
left = dfs(node.left) right = dfs(node.right)
得到左右子树的两种状态收益,作为当前节点计算的基础。
3. 如何根据左右子树状态计算当前节点状态?
# 不偷当前节点,左右子树可以偷或不偷,取最大
val_0 = max(left[0], left[1]) + max(right[0], right[1])
# 偷当前节点,左右子树节点不能偷,只能取它们“不偷”的收益
val_1 = node.val + left[0] + right[0]4. 为什么“偷当前节点”时,只能加上左右子树“不偷”时的收益?
因为题目限制:不能同时偷相邻节点,偷了当前节点,就不能偷它的左右孩子。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:dp = self.traversal(root) return max(dp)def traversal(self, node):if not node:return (0, 0) # 空节点返回 (不偷=0, 偷=0)#先递归左右子树left = self.traversal(node.left)right = self.traversal(node.right)#再计算当前节点的两个状态:偷或不偷 left[0]:不偷左孩子时的最大收益 left[1]:偷左孩子时的最大收益val_0 = max(left[0], left[1]) + max(right[0], right[1]) #不偷当前val_1 = node.val + left[0] + right[0] #偷return (val_0, val_1)
今天就结束啦,第三道题动态规划跟二叉树的后续遍历做了一下结合! 对我稍微吃力了一些,还得温故而知新呀!
