当前位置：首页 > news >正文

js多边形算法：获取多边形中心点，且必定在多边形内部

news 2025/7/26 12:35:20

前言

已有《js多边形算法：多边形缩放、获取中心、获取重心/质心、判断是否在多边形内、判断点排序是否顺时针等》，可以参考；

现有的获取多边形中心点，中心点不一定在多边形内部，例如凹多边形；
现在需要获取中心点，如果中心点不在多边形内部，则返回一个尽可能在中心点附近且在多边形内部点；

思路

1、获取多边形中心点，如果在多边形内部则返回中心点；
2、否则，获取多边形包围盒中心点，如果在多边形内部则返回包围盒中心点；
3、否则，从包围盒中心点按“包围盒中心指向多边形中心、垂直向上、垂直向下、水平向左、水平向右”顺序发射射线，获取射线和多边形的所有交点，穷尽所有交点组成的线段，若线段中心点在多边形内部则返回中心点；

例子

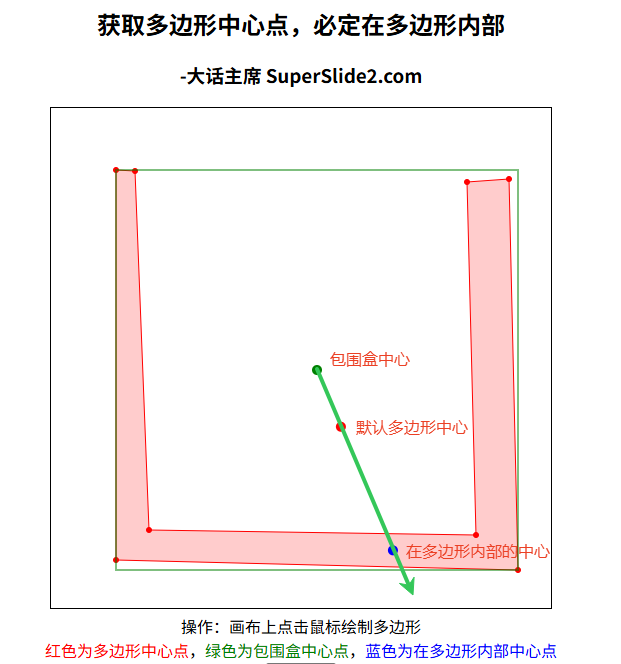
在这里插入图片描述

如上图，红色块为多边形，绿色边框为包围盒，红色的多边形中心点不在多边形内部，包围盒中心点也不在多边形内部，这时候从包围盒中心点垂直向下发射射线，和多边形相交2个点，再取2个交点的中心点作为多边形内部中心点！

页面效果

在这里插入图片描述

源码

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>Polygon Center Point</title><style>body {text-align: center;}canvas {border: 1px solid black;}</style></head><body><h2>获取多边形中心点，必定在多边形内部</h2><h3>-大话主席 SuperSlide2.com</h3><canvas id="canvas" width="500" height="500"></canvas><div>操作：画布上点击鼠标绘制多边形</div><div><span style="color: red">红色为多边形中心点</span>，<spanstyle="color: green">绿色为包围盒中心点</span>，<span style="color: blue">蓝色为在多边形内部中心点</span></div><div><button id="clearButton">重新绘制</button></div><div id="curPoint"></div><script>const canvas = document.getElementById("canvas");const ctx = canvas.getContext("2d");const clearButton = document.getElementById("clearButton");let polygon = []; // 多边形的点// 绘制点function drawPoint(center, color = "blue", radius = 5) {ctx.beginPath();ctx.arc(center.x, center.y, radius, 0, Math.PI * 2);ctx.fillStyle = color;ctx.fill();}// 绘制多边形function drawPolygon(polygon,color = "red",fillColor = "rgba(255, 0, 0, 0.2)") {ctx.beginPath();ctx.moveTo(polygon[0].x, polygon[0].y);for (let i = 1; i < polygon.length; i++) {ctx.lineTo(polygon[i].x, polygon[i].y);}ctx.closePath();ctx.strokeStyle = color;ctx.stroke();if (fillColor) {ctx.fillStyle = fillColor;ctx.fill();}}// 绘制多边形顶点function drawPolygonPoints(polygon) {for (let i = 0; i < polygon.length; i++) {drawPoint(polygon[i], "red", 3);}}// 绘制包围盒function drawBoundingBox(polygon) {const box = getBoundingBox(polygon);drawPolygon(box, "green");}// 计算多边形的中心点（质心）function getPolygonCenter(points) {if (!Array.isArray(points) || points.length < 3) {console.error("多边形坐标集合不能少于3个");return;}const result = { x: 0, y: 0 };let area = 0;for (let i = 1; i <= points.length; i++) {const curX = points[i % points.length].x;const curY = points[i % points.length].y;const nextX = points[i - 1].x;const nextY = points[i - 1].y;const temp = (curX * nextY - curY * nextX) / 2;area += temp;result.x += (temp * (curX + nextX)) / 3;result.y += (temp * (curY + nextY)) / 3;}result.x /= area;result.y /= area;return result;}// 判断点是否在多边形内function isPointInPolygon(point, polygon) {let inside = false;for (let i = 0, j = polygon.length - 1; i < polygon.length; j = i++) {const xi = polygon[i].x,yi = polygon[i].y;const xj = polygon[j].x,yj = polygon[j].y;const intersect =yi > point.y !== yj > point.y &&point.x < ((xj - xi) * (point.y - yi)) / (yj - yi) + xi;if (intersect) inside = !inside;}return inside;}/*** 获取多边形的包围盒中心点* @param {Array} polygon 多边形点集合* @return {Object} 包围盒中心点*/function getBoundingBoxCenter(polygon) {const box = getBoundingBox(polygon);return {x: (box[0].x + box[2].x) / 2,y: (box[0].y + box[2].y) / 2,};}/*** 获取多边形包围盒坐标集合，返回[左上, 右上, 右下, 左下]* @param {Array<Point>} polygon 多边形点数组* @returns {Array<Point>} 包围盒点数组*/function getBoundingBox(polygon) {let minX = Infinity,maxX = -Infinity,minY = Infinity,maxY = -Infinity;polygon.forEach((p) => {minX = Math.min(minX, p.x);maxX = Math.max(maxX, p.x);minY = Math.min(minY, p.y);maxY = Math.max(maxY, p.y);});return [{ x: minX, y: minY },{ x: maxX, y: minY },{ x: maxX, y: maxY },{ x: minX, y: maxY },];}/*** 获取多边形中心点，必定在多边形内部* 包围盒中心点按顺序从垂直向上下左右发射射线，取射线和多边形交点成线段的中心点坐标* @param {Array<Point>} polygon 多边形顶点数组* @returns {Point} 中心点*/function getPolygonCenterInPolygon(polygon) {const center = getPolygonCenter(polygon);if (isPointInPolygon(center, polygon)) {console.log("质心在多边形内，返回质心");return center;}const boxCenter = getBoundingBoxCenter(polygon);if (isPointInPolygon(boxCenter, polygon)) {console.log("包围盒中心在多边形内，返回包围盒中心");return boxCenter;}const directions = [{ x: center.x - boxCenter.x, y: center.y - boxCenter.y }, // 质心指向包围盒中心方向{ x: 0, y: -1 }, // 垂直向上{ x: 0, y: 1 }, // 垂直向下{ x: -1, y: 0 }, // 水平向左{ x: 1, y: 0 }, // 水平向右];const intersections = [];for (let d = 0; d < directions.length; d++) {const direction = directions[d];const rayStart = boxCenter;const rayEnd = {x: rayStart.x + direction.x * 9999,y: rayStart.y + direction.y * 9999,};const interPoints = getLinePolygonIntersections(polygon, [rayStart,rayEnd,]);if (interPoints.length < 2) continue;// 遍历所有交点组成的线段，取线段中心点，若中心点在多边形内则返回中心点for (let i = 0; i < interPoints.length; i++) {for (let j = i + 1; j < interPoints.length; j++) {// 取两个交点作为线段const p1 = interPoints[i];const p2 = interPoints[j];const midpoint = {x: (p1.x + p2.x) / 2,y: (p1.y + p2.y) / 2,};if (isPointInPolygon(midpoint, polygon)) {console.log("返回线段交点的中点", midpoint);return midpoint;}}}}return null;}/*** 获取线段和多边形的交点集合* @param {Array<Point>} polygon 多边形顶点数组* @param {Array<Point>} line 线段，[开始点，结束点]* @returns {Array<Point>} 交点数组*/function getLinePolygonIntersections(polygon, line) {const intersections = [];const lineStart = line[0];const lineEnd = line[1];const n = polygon.length;for (let i = 0; i < n; i++) {const p1 = polygon[i];const p2 = polygon[(i + 1) % n];const intersection = get2LinesIntersection(p1,p2,lineStart,lineEnd);if (intersection) {intersections.push(intersection);}}// 去重return uniqueArray(intersections);}/** 数组去重，高性能* @param {Array} arr 数组，支持数字、对象、字符串*/function uniqueArray(arr) {return Array.from(new Set(arr.map((item) => JSON.stringify(item)))).map((item) => JSON.parse(item));}/*** 获取两条线段交点* @param {Point} P1 线段1的起点* @param {Point} P2 线段1的终点* @param {Point} P3 线段2的起点* @param {Point} P4 线段2的终点* @return {Point | null} 交点*/function get2LinesIntersection(P1, P2, P3, P4) {const denom =(P2.x - P1.x) * (P4.y - P3.y) - (P2.y - P1.y) * (P4.x - P3.x);if (denom === 0) return null; // 两线段平行或重合const t =((P3.x - P1.x) * (P4.y - P3.y) - (P3.y - P1.y) * (P4.x - P3.x)) /denom;const s =((P3.x - P1.x) * (P2.y - P1.y) - (P3.y - P1.y) * (P2.x - P1.x)) /denom;if (t >= 0 && t <= 1 && s >= 0 && s <= 1) {return { x: P1.x + t * (P2.x - P1.x), y: P1.y + t * (P2.y - P1.y) };}return null;}// 清空画布function clearCanvas() {ctx.clearRect(0, 0, canvas.width, canvas.height);polygon = [];}// 处理点击事件canvas.addEventListener("click", (e) => {const x = e.offsetX;const y = e.offsetY;polygon.push({ x, y });drawAll();});// 处理点击事件canvas.addEventListener("mousemove", (e) => {const x = e.offsetX;const y = e.offsetY;document.getElementById("curPoint").innerText = `${x},${y}`;});function drawAll() {ctx.clearRect(0, 0, canvas.width, canvas.height);drawPolygonPoints(polygon);if (polygon.length < 3) return;drawPolygon(polygon);// 默认中心点const polygonCenter = getPolygonCenter(polygon);drawPoint(polygonCenter, "red");// 包围盒中心点const boxCenter = getBoundingBoxCenter(polygon);drawPoint(boxCenter, "green");// 包围盒drawPolygon(getBoundingBox(polygon), "green", null);// 必在多边形内部的中心点const intersectionCenter = getPolygonCenterInPolygon(polygon);drawPoint(intersectionCenter, "blue");}// 清除画布按钮clearButton.addEventListener("click", () => {clearCanvas();});</script></body>
</html>