轮盘赌算法
目录
- 背景
- 什么是轮盘赌
- 轮盘赌的设计
- 轮盘赌过程
- python代码
- 应用
背景
在现实生活中,我们尝尝需要一些简单小巧易操作的方法来做出决定而不是直接一拍脑门就决定的,如抓阄,就是一种比较古老的选择方式,轮盘赌则是西方人发明的一种选择方式。在一些智能算法如蚁群算法,遗传算法等中都有用到这种思想,轮盘赌常被用来设计随机选择算法,其目的是为了让个体被选中的概率适配个体在总体中的适应度,这一点很符合达尔文的优胜劣汰原则,如果一个个体适应度低,那么,这个个体配偶权可能被剥夺,多么痛的领悟。
什么是轮盘赌
轮盘赌全名叫轮盘赌博游戏,常见于地下赌场及网络赌场,其核心道具就是轮盘。轮盘赌的玩法是通过预测旋转轮盘后小球落位的数字或颜色进行下注,有美式与欧式两种主要类型。我们不去细究轮盘赌在拉斯维加斯还有澳门的作用,我们重点看看轮盘赌巧妙设计以及在智能算法中的作用。

轮盘赌的设计
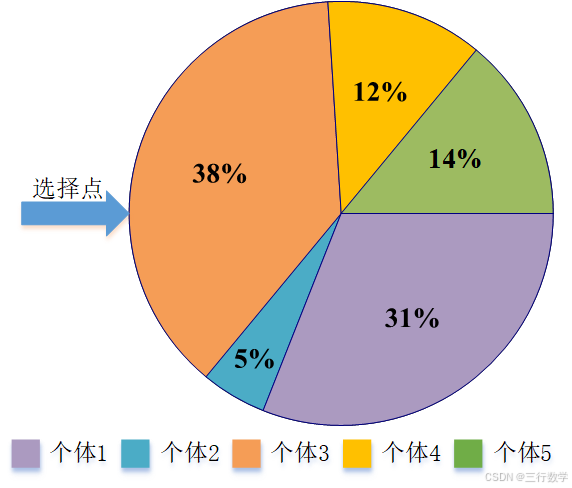
如上图所示,假设整体由5个个体组成,现在要随机从中选择一个个体进行后续操作,你会选谁呢?
简单做一个转盘,旋转这个盘子,直到转盘停止时,看指针停止在哪一块上,就选中指针所指的那个个体,很显然个体3有更多机会被选中。如果每个个体的适应度都一样,那么有均等机会被选中,但事实上,每个个体是有差异性的,称为个体的适应度差异,往往通过适应度函数来体现,适应度函数可以理解为该个体在特定环境下的性能或优劣程度。上图已经刻画出每个个体的适应度了,到此为此,我们已经知道如何通过选择转盘来选择了,称此时的选中概率为选择概率,选择谁的可能性大,有多大,选择谁的可能性小,有多小,但是你要设计一个映射让计算机随机生成一个东西就能锚定其中某个个体,而且锚定的与人类选择要一致,既选择概率与区间跨度对应起来了,这就是计算机模拟,于是乎,我们计算出累计概率
| 个体 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 选择概率 | 0.31 | 0.05 | 0.38 | 0.12 | 0.14 |
| 累计概率 | 0.31 | 0.36 | 0.74 | 0.86 | 1 |
| 区间跨度 | [0,0.31] | [0.31,0.36] | [0.36,0.74] | [0.74,0.86] | [0.86,1] |
有了累计概率,我们就可以从0到1进行切分,切分成一个一个区间,做一个序,接着,产生一个[0, 1]之间的随机数。然后,根据这个随机数落在哪个区间就选择对应个体。若为随机数是0.02,则落在第一个区间,则选择个体1,若随机数为0.56,则落在第三个区间,选择个体3,如果随机数是0.97,则选择第5个个体,这样给一个随机选择一个个体,给一个随机数选择一个个体,由于给的随机数是随机的,那么选择个体也是随机的,也就是说你从任何一个个体开始计算累计概率都是一样的,轮盘赌算法与个体的排列顺序有关;
轮盘赌过程
1,确定总体中每个个体,计算每个个体的适应度;
2,归一化适应度,使得它们的总和为1,这样做是为了将适应度值的占比转换为被选择的概率
选择概率=(每个个体适应度/所有个体适应度之和)
3,计算累积概率:从第一个个体开始,逐个累加每个个体的归一化适应度值,得到每个个体对应的累积概率。
4,选择个体:根据某种随机方法(如随机数生成器),产生一个[0, 1]之间的随机数。然后,根据这个随机数的大小,选择对应个体
python代码
知道轮盘赌是怎么回事,也知道怎么一步一步来进行选择了,下面用python脚本模拟轮盘赌
import random def rws():rnd = random.random() #产生0~1之间随机数unit = [1,2,3,4,5] #个体p = [0.31, 0.05, 0.38, 0.12, 0.14] #个体适应度sm = 0 #累计概率idx = 0 #被选择序号for i in range(len(p)): #对适应度循环sm += p[i] #计算累计概率if rnd <=sm: #如果所选随机数小于累计概率,则选中idx= i #选择第i个个体breakreturn unit[idx]
if __name__=="__main__":result = rws()print(result)
应用
除了赌博,轮盘赌在蚁群算法的蚂蚁选择,在遗传算法中的父代筛选过程中都大放异彩,除此之外,你还可以用轮盘赌和你好朋友去赌一赌运气。
