【算法-图论】图的存储
【算法-图论】图的存储
在图论中,我们应该如何存储一个图?每种存图的方法有什么优点,有什么缺点?这篇文章将会让你找到答案
1. 邻接表
邻接表是由一个静态的数组套动态的数组构成的。我们都知道动态数组的空间会随着数组的大小进行改变,可长可短,还可以自动释放一些无需的闲置空间,而外面的静态数组也可能对于一些节点空间小,一些节点空间大
当我们定义了一个邻接矩阵 GGG 时,GiG_iGi 则表示从 iii 号节点经过一条边到达的节点所构成的集合,我们只要遍历集合,就相当于遍历了以 iii 号为起点的边
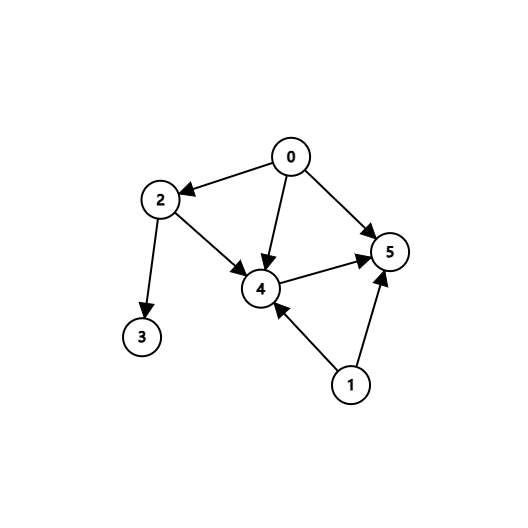
例如上面的这个有向图可以写成这样的邻接表
G0={2,4,5}G1={4,5}G2={3,4}G3=∅G4={5}G5=∅
G_0 = \{2, 4, 5\} \\
G_1 = \{4, 5\} \\
G_2 = \{3, 4\} \\
G_3 = \emptyset \\
G_4 = \{5\} \\
G_5 = \emptyset
G0={2,4,5}G1={4,5}G2={3,4}G3=∅G4={5}G5=∅
此外,如果这个图是无向图,可以看成两个相连的节点互相连接
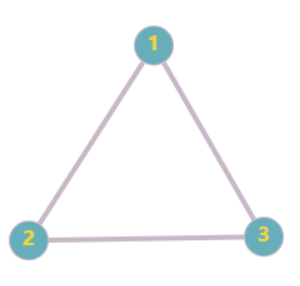
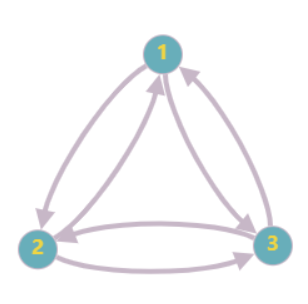
如果还想保存权值的话,就在里面的动态数组中套一个结构体,一个是要到的点,另一个是到那个点的边的权值
以下是对于有权值有向图的邻接表的代码
const int V = 1005; // 点的数量struct EdgeNode {int v, w; // 到的地方和权值
};vector<EdgeNode> G[V];void AddEdge (int u, int v, int w) {G[u].push_back({v, w});
}
2. 邻接矩阵
它使用的是要一个二维静态数组,Gu,vG_{u, v}Gu,v 表示从 uuu 到 vvv 是否有边链接,如果有边为 111,否则没边为 000。对于有权值的边而言,Gu,vG_{u, v}Gu,v表示为从 uuu 到 vvv 连接的边权,如果没边则 Gu,v=∞G_{u, v} = \inftyGu,v=∞,另外,Gi,i=0G_{i, i} = 0Gi,i=0
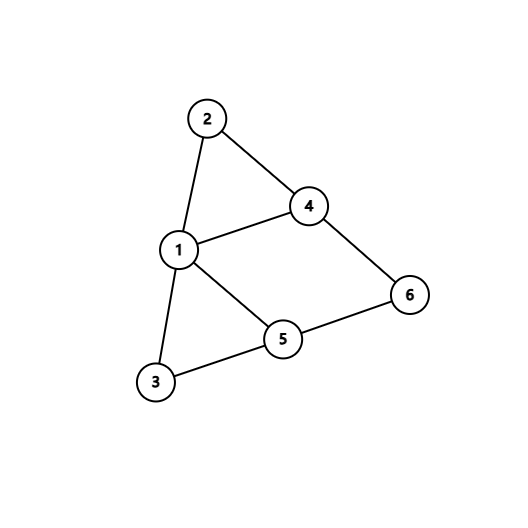
对于这个图,那么它的邻接矩阵就是:
[011110100100100010110001101001000110]
\begin{bmatrix}
0 & 1 & 1 & 1 & 1 & 0 \\
1 & 0 & 0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 & 0 & 1 \\
1 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 1 & 0 \\
\end{bmatrix}
011110100100100010110001101001000110
其中,我们不难发现:矩阵始终是个方阵,且大小为 ∣V∣2|V|^2∣V∣2
这是有权值无向图的邻接矩阵的写法:
const int V = 1005; // 点的个数int G[V][V]; // 邻接矩阵void AddEdge (int u, int v, int w) {G[u][v] = G[v][u] = w;
}int main () {memset(G, 0x3f, sizeof(G));
}
3. 边表
边表,也叫做链式前向星,它使用一个大小 2∣E∣2|E|2∣E∣ 的一维数组 EdgeEdgeEdge 存储边,还有一个大小为 ∣V∣|V|∣V∣ 的数组 HeadHeadHead 表示头指针。其中,EdgeEdgeEdge 的每一个元素实际上存储了三个属性:边连接哪个点、边的权值和同样以这个边的起点作为起点的其他的边,用于遍历所有的边。HeadHeadHead 存储着应该从哪里开始遍历以某个点作为起点的所有点,作为遍历的开端。实际编程时,我们可以倒着连接
这是加边用的函数
const int ARRMAX = 100005;struct GrephEdge {int v; // 去哪个点int w; // 权值int nxt; // 下一个边
} Edge[ARRMAX << 1];
int cnt;
int Head[ARRMAX];void AddEdge (int u, int v, int w) { // 插入以 u 为起点,v 为终点,权值为 w 的边Edge[cnt] = {v, w, Head[u]}; // 边的增加Head[u] = cnt++; // 改变头指针
}
