Y1第4课题解(A~E)
第一题:
题目: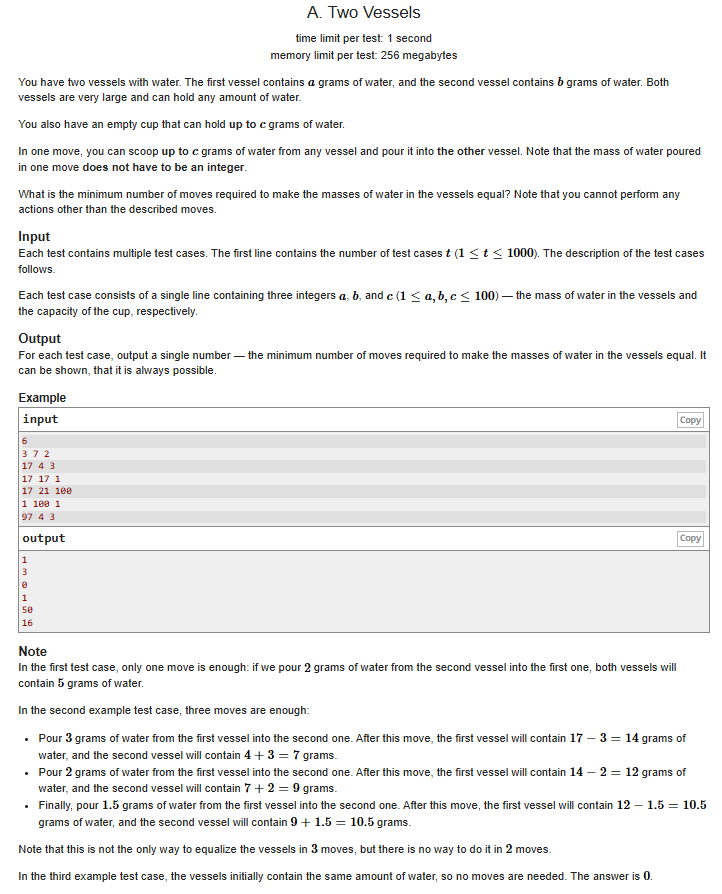
思路:
我们可以发现当在a拿c到b其实可以让他们差值减少2c,所以对a和b的差值除以2c向上取整即可
代码:
#include<bits/stdc++.h>
using namespace std;
// 定义全局变量,用于存储两个容器的水量和杯子的容量
int a, b, c;
int main(){// 存储测试用例的数量int n;// 输入测试用例的数量cin >> n;// 遍历每个测试用例for(int i = 1; i <= n; i++){// 输入当前测试用例的 a, b, ccin >> a >> b >> c;// 计算需要转移的水量的一半(因为要让两个容器水量相等,所以需要将差值的一半从多的容器转移到少的容器)double e = abs(b - a) / 2.0;// 计算需要的最少移动次数:将 e 除以 c 并向上取整// 这里使用 ceil 函数计算向上取整,然后转换为 int 类型输出cout << (int)ceil(e / c) << endl;}return 0;
}第二题:
题目:
思路:
我们可以发现我们当前能到达最远是 d+(s-1)/ 2,然后就是找这些里面最小的值即可
代码:
#include<bits/stdc++.h>
using namespace std;// 定义全局变量,用于存储测试用例的数量和陷阱的参数
int t, n;
// 存储每个陷阱的关键值
int a[105];int main(){// 输入测试用例的数量cin >> t;// 遍历每个测试用例for(int i = 1; i <= t; i++){// 输入当前测试用例的陷阱数量cin >> n;// 遍历每个陷阱,计算其关键值并存储在数组 a 中for(int i = 1, x, y; i <= n; ++i) {// 输入陷阱的位置 x 和激活时间 ycin >> x >> y;// 计算陷阱的关键值:x + floor((y - 1) / 2)// 这个值表示陷阱激活前,最多可以到达的房间号a[i] = x + (int)floor((y - 1) / 2.0);}// 初始化最小值为一个很大的数int minn = 0x3f3f3f3f;// 从最后一个陷阱开始向前遍历,找到最小的关键值for(int i = n; i >= 1; i--){minn = min(minn, a[i]);}// 输出当前测试用例的最大安全房间号cout << minn << endl;}return 0;
}第三题:
题目: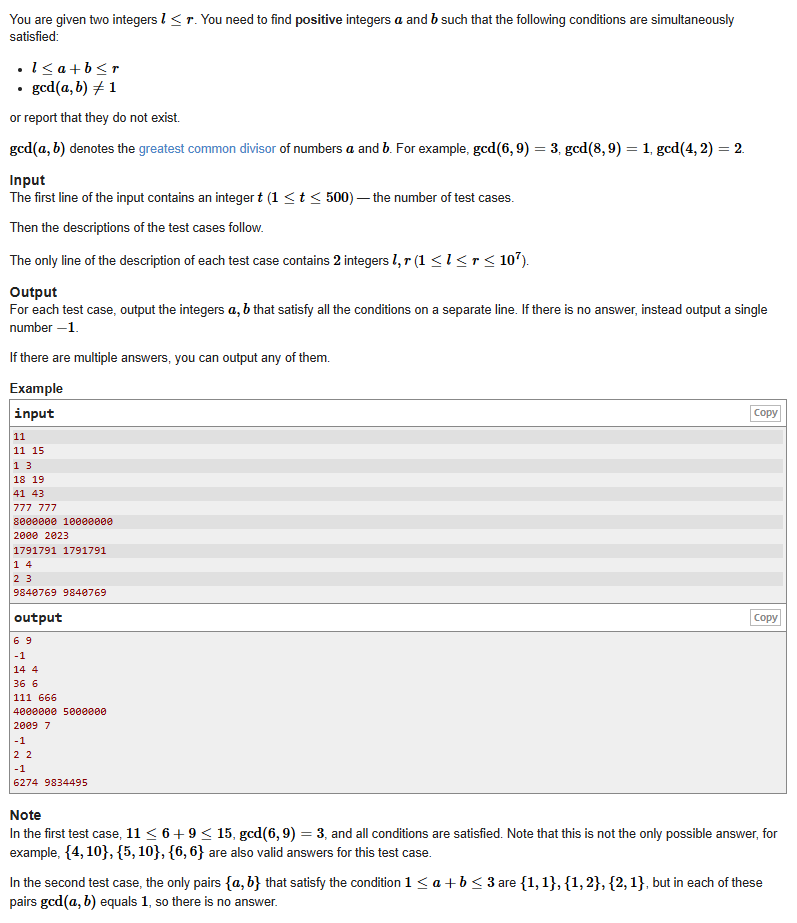
思路:
令i = a+b,枚举i,然后找到i的因子,就直接输出,遍历结束,找不到的话,表明没有符合题意得结果,输出-1即可;
代码:
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
const ll N = 1e7 + 10;// 定义变量,a 和 b 分别表示当前测试用例的 l 和 r,t 表示测试用例的数量
ll a, b, t;int main() {// 输入测试用例的数量cin >> t;while (t--) {// 输入当前测试用例的 l 和 rcin >> a >> b;// 如果 r < 4,直接输出 -1,因为无法找到满足条件的 a 和 bif (b < 4) {cout << -1 << endl;continue;}// 如果 r - l > 0,或者 r 是偶数,或者 l 是偶数// 这种情况下,直接输出两个相等的数,它们的和在 [l, r] 范围内,且 gcd 大于 1if (b - a || b % 2 == 0 || a % 2 == 0) {// 计算两个相等的数,它们的和为 r(如果 r 是偶数)或 r - 1(如果 r 是奇数)ll mid = (b - (b & 1)) >> 1;cout << mid << " " << mid << endl;} else {// 标记是否找到满足条件的 a 和 bbool judge = 0;// 计算 l 的平方根,用于优化循环int si = sqrt(a);// 遍历可能的因数,寻找满足条件的 a 和 bfor (int j = 2; j <= si; j++) {// 如果 j 是 a 的因数if ((a - j) % j == 0) {// 标记找到解judge = 1;// 输出解cout << j << " " << a - j << endl;break;}}// 如果没有找到解,输出 -1if (!judge) {cout << "-1" << endl;}}}return 0;
}第四题:
题目:
思路:
本题最重要的就是去除px和py重复的部分;重复个数 : c : n / lcm(x,y);
lcm() : 最小公倍数;
那么x要取得个数 : a = n / x - c;
y要取得个数 ; b = n / y - c;
然后就是等差数列求和的思想分别按x取最大,y取最小求出答案;
代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
// 定义变量,T 表示测试用例的数量,n, x, y 分别表示当前测试用例的参数
int T;
ll n, x, y;
// 计算最大公约数
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
// 计算最小公倍数
ll lcm(ll a, ll b) { return a / gcd(a, b) * b; }
int main() {// 输入测试用例的数量scanf("%d", &T);while (T--) {// 输入当前测试用例的 n, x, yscanf("%lld %lld %lld", &n, &x, &y);// 计算只被 x 整除的数的个数ll num1 = n / x - n / lcm(x, y);// 计算只被 y 整除的数的个数ll num2 = n / y - n / lcm(x, y);// 计算最大可能的分数// 最大分数 = 只被 x 整除的数的和 - 只被 y 整除的数的和// 只被 x 整除的数的和是 (n + (n - num1 + 1)) * num1 / 2// 只被 y 整除的数的和是 (1 + num2) * num2 / 2printf("%lld\n", (n + (n - num1 + 1)) * num1 / 2 - (1 + num2) * num2 / 2);}return 0;
}第五题:
题目:
思路:
每次修改都是直接异或上区间和就行了,那么修改和查询的复杂度都是 O(1) 。
代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e5 + 10;
// 定义数组 a,用于存储输入的整数数组
ll a[N];
int main() {// 关闭同步,加速输入输出ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// 测试用例的数量ll t;cin >> t;while (t--) {// 数组长度ll n;cin >> n;// 输入数组 afor (int i = 1; i <= n; i++) cin >> a[i];// 输入二进制字符串 sstring s;cin >> s;// 初始化 ans 和 ansz,分别存储 s 中字符为 '1' 和 '0' 的位置对应的异或和ll ans = 0, ansz = 0;for (int i = 0; i < s.length(); i++) {if (s[i] - '0') {// 如果当前字符是 '1',更新 ansif (!ans) ans = a[i + 1];else ans ^= a[i + 1];} else {// 如果当前字符是 '0',更新 anszif (!ansz) ansz = a[i + 1];else ansz ^= a[i + 1];}}// 计算前缀异或数组for (int i = 1; i <= n; i++) {a[i] ^= a[i - 1];}// 查询的数量ll q;cin >> q;while (q--) {// 查询类型ll op;cin >> op;if (op == 1) {// 翻转区间 [x, y] 的字符ll x, y;cin >> x >> y;// 更新 ans 和 anszans ^= a[x - 1] ^ a[y];ansz ^= a[x - 1] ^ a[y];} else {// 查询字符为 t 的位置对应的异或和int t;cin >> t;if (t) cout << ans << ' ';else cout << ansz << ' ';}}cout << '\n';}return 0;
}