【算法】递归、搜索与回溯算法入门

递归

什么是递归

通俗来讲，也就是函数自己调用自己的情况。像二叉树的遍历、快排算法、归并算法等。

为什么会用到递归

本质：解决主问题的时候会衍生出相同的子问题，解决子问题的时候又衍生出相同的子问题。

主问题 -> 相同的子问题
子问题 -> 相同的子问题

一直往复…

如何理解递归

第一层次去理解：画递归展开的细节图
第二层次去理解：编写和理解二叉树中的题目
第三层次去理解：宏观的看待递归的过程

我们要在第三层去理解：

1. 不要在意递归的细节展开图
2. 把递归的函数当成一个黑盒（过程是怎么样的不用管，看不到内部过程）
3. 相信这个黑盒一定能够完成这个任务

如何写好一个递归

1. 先找到相同的子问题！！！！！-> 决定了函数头的设计
2. 只关心某一个子问题是如何解决的 -> 函数体的书写
3. 注意一下递归函数的出口即可

把数据结构中二叉树的题目，试着用第三层的方式去理解一下。

搜索 vs 深度优先遍历 vs 深度优先搜索 vs 宽度（广度）优先遍历 vs 宽度（广度）优先搜索 vs 暴搜

搜索其实就是把整个解空间遍历一遍，本质就是暴力枚举一遍所有的情况。也就是暴搜。

深度优先遍历 vs 深度优先搜索（dfs）

通俗理解：一条道走到黑，走到不能再走时返回，遇到分支，和前面一样的操作。

遍历是形式，搜索是目的。所以他们两可以理解为一个东西。

宽度（广度）优先遍历 vs 宽度（广度）优先搜索（bfs）

通俗理解：一层一层剥开，也就是一层一层的去遍历。

遍历是形式，搜索是目的。所以他们两可以理解为一个东西。

关系图

拓展搜索问题

全排列问题：就是高中数学学的排列组合的问题，比如1，2，3，有哪几种排列方式。如果数少还能列的出来，但是数一多就很容易一漏掉一些情况。

树状图 (决策树)

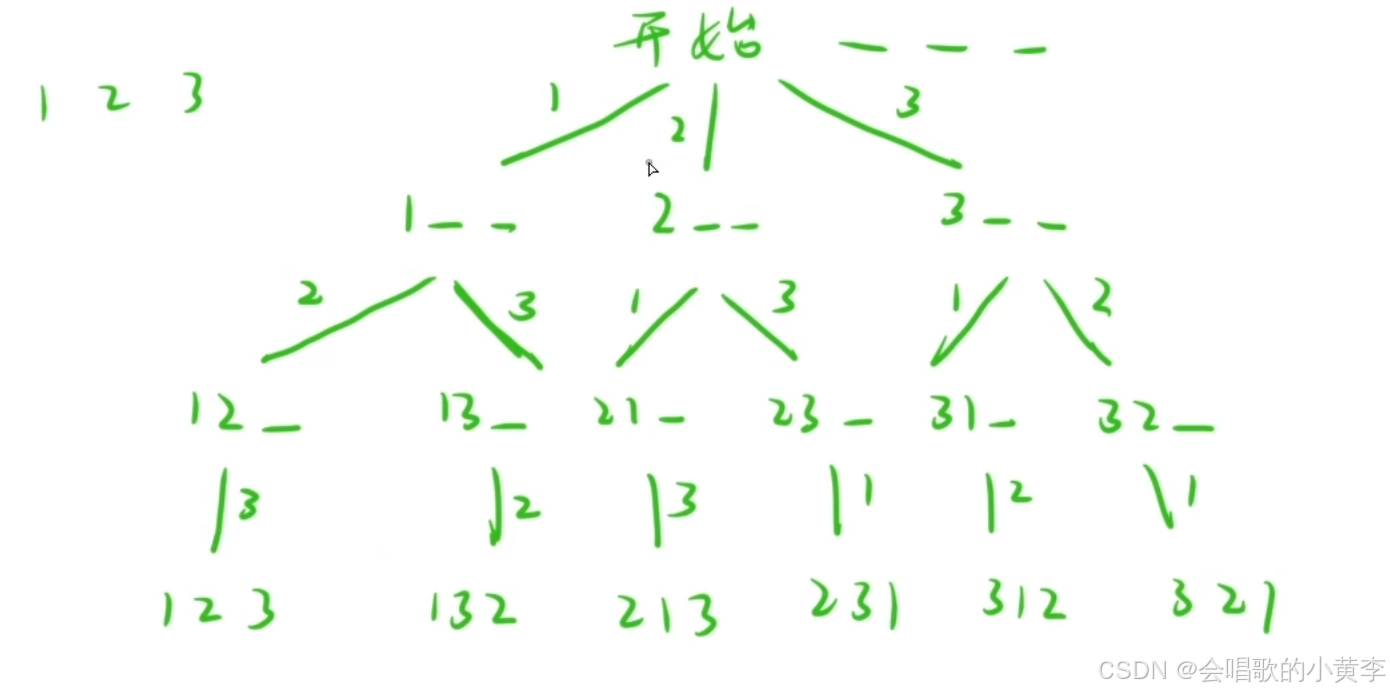
注意：不要局限于认为只有二叉树和图这些问题才能使用dfs和bfs，只要整个问题能用决策树的方式画出来的话，就能使用。

回溯和剪枝

回溯其实就是深搜里的一个小分支。

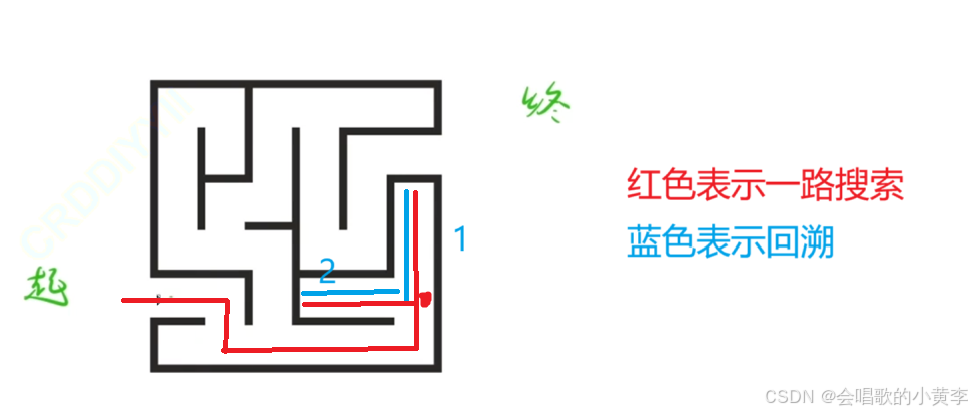
简单理解一下回溯，就是尝试某种情况的时候，发现走不通，返回到上一级的这个操作。也就是图中红色按1走的然后返回到红点的过程。
再简单理解一下剪枝，就是按1返回到红点后再走到按2走，发现行不通再返回到红点，此时往上往下都有路线，但是往上走已经尝试过了，不用再走了。其实就是在分叉路口有两种选择的时候，但是我们已经明确知道了其中一个选择不是我们最终想要的结果的时候，我们就把这个结果给略过。