408——数据结构(第二章 线性表)
2.1线性表的定义和基本操作
2.1.1 线性表的定义
线性表是具有相同数据类型的n(n>=0)n(n>=0)n(n>=0)个数据元素的有限序列,其中nnn为表长,当n=0n=0n=0时线性表十一个空表。
若用LLL命名,则其一般表示为 L=(a1,a2,...,an)L=(a_1,a_2,...,a_n)L=(a1,a2,...,an)
a1a_1a1是表头元素,ana_nan是表尾元素。除了第一个元素外,每个元素有且仅有一个直接前驱,除了最后一个元素外,每个元素有且仅有一个直接后继。
2.1.2 线性表的基本操作
一个数据结构的基本操作是指其最核心、最基本的操作。其他较复杂的操作可通过调用其基本操作来实现。线性表的主要操作如下:
- InitList(&L):初始化表。构造一个空的线性表。
- Length(L):求表长。返回线性表 L 的长度,即 L 中数据元素的个数。
- LocateElem(L,e):按值查找操作。在表 L 中查找具有给定关键字值的元素。
- GetElement(L,i):按位查找操作。获取表 L 中第 i 个位置的元素的值。
- ListInsert(&L,i,e):插入操作。在表 L 中的第 i 个位置上插入指定元素 e。
- ListDelete(&L,i,&e):删除操作。删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值。
- PrintList(L):输出操作。按前后顺序输出线性表 L 的所有元素值。
- Empty(L):判空操作。若 L 为空表,则返回 true,否则返回 false。
- DestroyList(&L):销毁操作。销毁线性表,并释放线性表 L 所占用的内存空间。
2.2线性表的顺序表示
2.2.1 顺序表的定义
顺序表–用顺序存储的方式实现线性表。把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由于存储单元的邻接关系来体现。
假设线性表的第一个元素的存放位置(地址)是LOC(L)LOC(L)LOC(L),则第二个元素的存放位置(地址)是LOC(L)+数据元素大小LOC(L)+数据元素大小LOC(L)+数据元素大小,则第三个元素的存放位置(地址)是LOC(L)+2∗数据元素大小LOC(L)+2*数据元素大小LOC(L)+2∗数据元素大小。
**如何知道一个数据元素的大小?可以使用sizeof(ElemType)**以此查看数据元素大小
小tips:
| 项目 | typedef | #define |
|---|---|---|
| 作用 | 为已有类型定义别名 | 定义宏、常量、代码片段 |
| 编译阶段 | 编译阶段生效 | 预处理阶段生效 |
| 是否有作用域 | 有(受作用域限制) | 无(全局文本替换) |
| 适合场景 | 定义复杂类型别名,例如结构体、指针等 | 定义常量、简单表达式、条件编译 |
| 是否能调试看到信息 | 可以(调试时仍显示原始类型) | 不能(调试时只看见替换后的结果) |
静态分配的顺序表
注: 静态分配的顺序表的表长一旦确认后不可该变。
#include<bits/stdc++.h>
using namespace std;
#define MaxSize 10 //定义最大长度
#define ElemType int //定义所需变量
typedef struct{ElemType data[MaxSize]; //用静态的“数组”存放数据元素int length; //顺序表的当前长度
}SqList; //顺序表的类型定义(静态分配方式)//顺序表的初始化
void InitList(SqList &L){for(int i=0;i<MaxSize;i++){L.data[i]=0;}L.length = 0; //不能省略
}int main()
{SqList L; //声明(定义)一个顺序表InitList(L); //初始化一个顺序表return 0;
}
动态分配的顺序表
#include<bits/stdc++.h>
using namespace std;
#define ElemType int //定义所需变量
#define InitSize 10 //顺序表初始长度
typedef struct{ElemType *data; int MaxSize; int length; //顺序表的当前长度
}SqList; //顺序表的类型定义(动态分配方式)//顺序表的初始化
void InitList(SqList &L){//使用malloc函数申请一片连续的存储空间L.data = (ElemType *)malloc(sizeof(ElemType)*InitSize);L.length = 0;L.MaxSize = InitSize;
}//增加动态顺序表的长度
void IncreaseSize(SqList &L,int len){int *p=L.data; L.data = (ElemType *)malloc(sizeof(ElemType)*(L.MaxSize+len));for(int i=0;i<L.length;i++){L.data[i]=p[i]; //将数据复制到新区域}L.MaxSize+=len;free(p); //释放与原来的内存空间
} int main()
{SqList L; //声明(定义)一个顺序表InitList(L); //初始化一个顺序表IncreaseSize(L,5); //增加5个长度return 0;
}
Key: 动态申请和释放内存空间。(使用malloc,free函数)
L.data = (ElemType *)malloc(sizeof(ElemType)*InitSize)
malloc函数返回一个指针,需要强制转换(ElemType *)为定义的数据元素指针
参数sizeof(ElemType)*InitSize中*是乘号。
顺序表特点:
随机访问,可在O(1)O(1)O(1)时间内找到第i个元素。
存储密度高,每个节点只存数据元素。
拓展容量不方便。
插入、删除操作不方便,需要移动大量元素。
2.2.2顺序表的基本操作
插入:
bool ListInsert(SqList &L,int i,ElemType e){if(i<1||i>L.length+1) //判断插入的位置是否有效return false;if(L.length>=MaxSize) //当前存储空间已满,不能插入return false;for(int j=L.length;j>=i;j--){//将第i个元素及之后的元素后移L.data[j]=L.data[j-1]; } L.data[i-1]=e; //在位置i处放入eL.length++; //长度+1return true;
}
时间复杂度分析:
最好情况:新元素插入到表尾,不需要移动元素
i=n+1i = n+1i=n+1,循环000次;
最好时间复杂度 = O(1)O(1)O(1)
最坏情况:新元素插入到表头,需要将原有的 (n)( n )(n) 个元素全部向后移动
i=1i = 1i=1,循环 nnn 次;
最坏时间复杂度 = O(n)O(n)O(n);
平均情况:假设新元素插入到任何一个位置的概率相同,即 (i=1,2,3,...,length+1)( i = 1, 2, 3, ..., \text{length} + 1 )(i=1,2,3,...,length+1)的概率都是 p=1n+1p = \frac{1}{n+1}p=n+11,平均循环次数 = p=1n+1n(n−1)2=n2p = \frac{1}{n+1}\frac{n(n-1)}{2}=\frac{n}{2}p=n+112n(n−1)=2n
平均时间复杂度 = O(n)O(n)O(n)
删除:
bool ListDlete(SqList &L,int i,int &e){if(i<1||i>L.length) //判断插入的位置是否有效return false;e = L.data[i-1]; //将删除的元素的值赋给efor(int j=i;j<L.length;j++){ //将第i个位置后的元素前移L.data[j-1]=L.data[j];}L.length--; //长度-1return true;
}
时间复杂度分析:
最好情况:新元素插入到表尾,不需要移动元素
i=ni = ni=n,循环000次;
最好时间复杂度 = O(1)O(1)O(1)
最坏情况:新元素插入到表头,需要将原有的 (n)( n )(n) 个元素全部向后移动
i=1i = 1i=1,循环 n−1n-1n−1 次;
最坏时间复杂度 = O(n)O(n)O(n);
平均情况:假设新元素插入到任何一个位置的概率相同,即 (i=1,2,3,...,length)( i = 1, 2, 3, ..., \text{length} )(i=1,2,3,...,length)的概率都是 p=1np = \frac{1}{n}p=n1,平均循环次数 = p=1nn(n−1)2=n−12p = \frac{1}{n}\frac{n(n-1)}{2}=\frac{n-1}{2}p=n12n(n−1)=2n−1
平均时间复杂度 = O(n)O(n)O(n)
按位查找:获取表L中的第i个位置的元素的值。
ElemType GetElem(SqList L,int i){return L.data[i-1];
}
时间复杂度 = O(1)O(1)O(1)
按值查找:在表L中查找具有给定关键字值得元素。
//在顺序表L中查找第一个元素值=e的元素,并返回其位序。
ElemType LocateElem(SqList L,ElemType e){for(int i=0;i<L.length;i++){if(L.data[i]==e)return i+1; //数组下标位i,其位序i+1}return 0; //退出循环,说明查找失败
}
注:
C语言中,结构体的比较不能直接使用"======"。
最好情况:目标在表头
循环111次, 最好时间复杂度 = O(1)O(1)O(1)
最坏情况:目标在表尾
循环 nnn 次,最坏时间复杂度 = O(n)O(n)O(n);
平均循环次数 = p=1nn(n+1)2=n+12p = \frac{1}{n}\frac{n(n+1)}{2}=\frac{n+1}{2}p=n12n(n+1)=2n+1
平均时间复杂度 = O(n)O(n)O(n)
2.3线性表的链式表示
2.3.1单链表的定义
定义:线性表的链式存储又称单链表,它是指通过一组任意的存储单元来存储线性表中的数据元素。为了建立数据元素之间的线性关系,对每个链表结点,除存放元素自身的信息之外,还需要存放一个指向其后继的指针。单链表结点结构如图所示,其中data为数据域,存放数据元素;next为指针域,存放其后继结点的地址。

单链表结点结构
优点:不要求大片连续空间,改变容量方便。
缺点:不可随机存取,要耗费一定空间存放指针。
初始化,不带头结点:
#include<bits/stdc++.h>
using namespace std;
#define ElemType int //定义所需变量
// LNode:结点 data:数据域 next: 指针域
typedef struct LNode{ //定义单链表结点类型ElemType data; //每个结点存放一个数据元素struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
//等价于
/*
struct LNode{ ElemType data; struct LNode *next;
}
typedef struct LNode LNode;
typedef struct LNode *Linklist;
*///初始化,不带头结点
bool InitList(LinkList &L){L = NULL; //空表,暂时没有任何结点(防止遗留的脏数据)return true;
}//判断单链表是否为空
bool Empty(LinkList L){return (L==NULL);
}
初始化,带头结点:
#include<bits/stdc++.h>
using namespace std;
#define ElemType int //定义所需变量
// LNode:结点 data:数据域 next: 指针域
typedef struct LNode{ //定义单链表结点类型ElemType data; //每个结点存放一个数据元素struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;//初始化,带头结点
bool InitList_take(LinkList &L){L = (LNode *)malloc(sizeof(LNode));//分配一个头结点if(L==NULL) //内存不足,分配失败return false;L->next = NULL; //相当于(*L).next 头结点之后暂时还没有结点return true;
}
//判断单链表是否为空
bool Empty_take(LinkList L){if(L->next==NULL)return true;elsereturn false;
}
强调这个是一个链表 --使用Linklist
强调这是一个结点 --使用LNode *
2.3.2 单链表的基本操作
按位序插入(带头结点): 在表L中的第i个位置上插入指定元素e
bool ListInsert(LinkList &L,int i,ElemType e){if(i<1)return false;LNode* p; //指针p指向当前扫描到的结点int j=0; //当前p指向的第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)while(p!=NULL && j<i-1){//循环找到第i-1个结点p = p->next;j++;}if(p==NULL)return false;LNode* s =(LNode* )malloc(sizeof(LNode));s->data=e;s->next=p->next;p->next=s; //将结点s连到preturn true; //插入成功
}
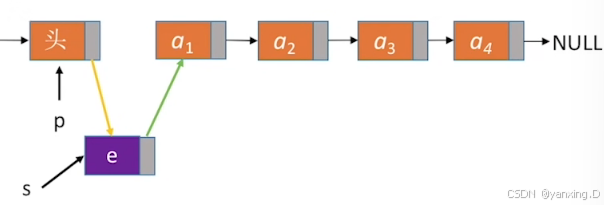
注: 虽然你只操作了 p,但 p 是从 L 开始向下遍历的,并且修改的是 p->next,也就是链表中某个结点的指针域。由于 L 是链表的头指针,所有的结点都是从 L 开始连接的,所以你插入的结点自然也就成为链表的一部分了。
按位序插入(不带头结点):
bool ListInsert(LinkList &L,int i,ElemType e){if(i<1)return false;if(i==1){LNode* s=(LNode* )malloc(sizeof(LNode));s->data=e;s->next=L;L=s;return true;}LNode* p; //指针p指向当前扫描到的结点int j=1; //当前p指向的第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)while(p!=NULL && j<i-1){//循环找到第i-1个结点p = p->next;j++;}if(p==NULL)return false;LNode* s =(LNode* )malloc(sizeof(LNode));s->data=e;s->next=p->next;p->next=s; //将结点s连到preturn true; //插入成功
}
指定结点的后插操作: 在p结点之后插入元素e
bool InsertNextNode(LNode* p,ElemType e){if(p==NULL)return false;LNode *s=(LNode *)malloc(sizeof(LNode));if(s==NULL)return false;s->data=e; //用结点s保存数据元素es->next=p->next;p->next=s; //将结点s连到p之后return true;
}
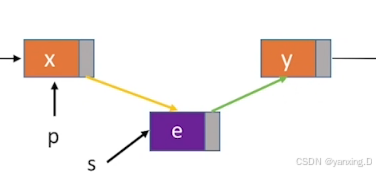
前插操作: 在p结点之前插入元素e
bool InsertPriorNode(LNode *p,LNode *s){if(p==NULL||s==NULL)return false;s->next=p->next;p->next=s; //s连接到p之后ElemType temp = p->data; //交换数据域的值p->data = s->data;s->data = temp;return true;
}
删除操作(带头结点): 删除表L中第i个位置的元素,并用e返回删除元素的值。
bool ListDelete(LinkList &L,int i,ElemType &e){if(i<1)return false;LNode* p; //指针p指向当前扫描到的结点int j=0; //当前p指向的第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)while(p!=NULL && j<i-1){//循环找到第i-1个结点p = p->next;j++;}if(p==NULL|| p->next == NULL)return false;LNode* q = p->next; //q指向被删除的结点e = q->data; //用e返回元素值p->next = q->next; //将*q结点从链中"断开"free(q); //释放空间return true;
}
删除指定结点p:
//删除指定结点
bool DeleteLNode(LNode *p){if(p==NULL|| p->next == NULL)return false;LNode *q = p->next;p->data = q->data; //等价于p->data = p->next->datap->next = q->next;free(q);return true;
}
查找(按位查找):
LNode *GetElem(LinkList L,int i){int j=1;LNode *p = L->next;if(i==0)return L;if(i<1)return NULL;while(p!=NULL && j<i){p=p->next;j++;}return p;
}
查找(按值查找): 找到数据域等于e的结点
LNode *LocateElem(LinkList L,ElemType e){if (L == NULL) return NULL;LNode *p= L->next; //从第一个结点开始查找数据域为e的结点while(p!=NULL&&p->data!=e){p=p->next;}return p; //找到返回该结点指针,否则返回NULL
}
求表长:
int Length(LinkList L){int len = 0;LNode* p = L;while(p->next != NULL){p = p->next;len++;}return len;
}
单链表的建立(尾插法):
Step1: 初始化一个单链表
Step2: 每次取一个数据元素,插入表头/表尾
//正向建立单链表
LinkList List_Taillnsert(LinkList &L){int x; L=(LNode*)malloc(sizeof(LNode));LNode *s,*r=L; //r为表尾指针cin>>x;while(x!=9999){ //设置一个安全词s=(LNode*)malloc(sizeof(LNode));s->data=x;r->next=s;r=s; //r指向新的表尾结点cin>>x;}r->next=NULL; //尾结点指针置空return L;
}
单链表的建立(头插法):
//逆向建立单链表(头插法)
LinkList List_HeadInsert(LinkList &L){LNode* s;int x;L=(LNode*)malloc(sizeof(LNode));L->next = NULL;cin>>x;while(x!=9999){s=(LNode*)malloc(sizeof(LNode));s->data=x;s->next = L->next;L->next = s;cin>>x;}return L;
}
2.3.3双链表
双链表:
在单链表的基础上再增加一个前驱指针域。
初始化:
typedef struct DNode{ElemType data;struct DNode *prior,*next;
}DNode,*DLinkList;//初始化
bool InitDLinkList(DLinkList &L){L = (DNode *)malloc(sizeof(DNode));if(L==NULL) //内存不足,分配失败return false;L->prior=NULL; //头结点的prior永远指向NULLL->next =NULL; //头结点之后暂时没有结点return true;
}
插入:
bool InsertNextDNode(DNode *p,DNode *s){if(p==NULL||s==NULL) //非法参数return false;s->next=p->next;if(p->next!=NULL) //如果p结点有后继结点p->next->prior=s;s->prior=p;p->next=s;return true;
}
删除: 删除p的后继结点q
//删除
bool DeleteNextDNode(DNode *p){if(p==NULL) //非法参数return false;DNode*q =p->next; //找到p的后继结点qif(q==NULL) //p没有后继return false;p->next=q->next;if(q->next!=NULL) //q结点不是最后一个结点q->next->prior=p;free(q); //释放节点空间return true;
}
2.3.4循环链表
循环单链表: 在单链表的基础上,其最后一个结点的指针不是NULL,而改为指向头结点,从而整个链表形成一个环。
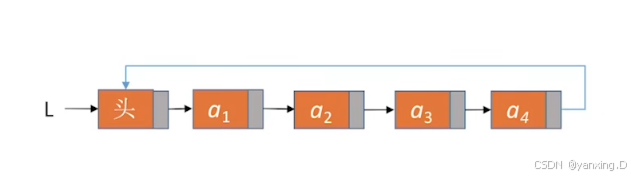
#include<bits/stdc++.h>
using namespace std;
#define ElemType int //定义所需变量
typedef struct LNode{ElemType data;struct LNode *next;
}LNode,*LinkList;//初始化
bool InitList(LinkList &L){L = (LNode*)malloc(sizeof(LNode));if(L==NULL)return false;L->next=L;return true;
}//判断是否为空
bool Empty(LinkList L){if(L->next == L)return true;else return false;
}//判断结点p是否为循环链表的表尾结点
bool isTail(LinkList L,LNode *p){if(p->next==L)return true;else return false;
}
循环双链表: 在双链表的基础上,表头结点的prior指向表尾结点;表为结点的next指向头结点。
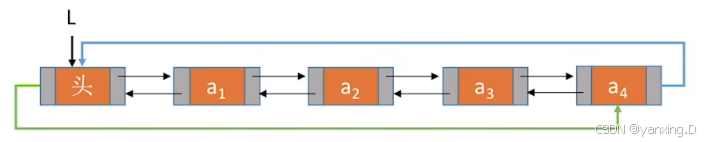
#include<bits/stdc++.h>
using namespace std;
#define ElemType int //定义所需变量
typedef struct DNode{ElemType data;struct DNode *prior,*next;
}DNode,*DLinkList;//初始化
bool InitDLinkList(DLinkList &L){L = (DNode *)malloc(sizeof(DNode));if(L==NULL) return false;L->prior=L; L->next =L; return true;
}bool Empty(DLinkList L){if(L->next == L)return true;else return false;
}bool isTail(DLinkList L,DNode *p){if(p->next==L)return true;else return false;
}
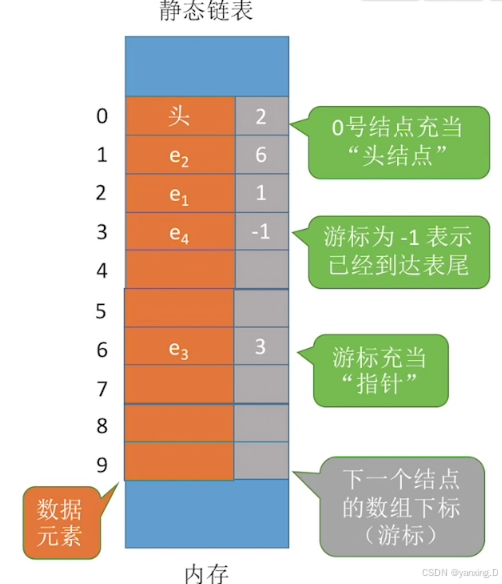
2.3.5静态链表
静态链表: 分配一整片连续的内存空间,各个结点集中安置。
#define ElemType int
#define MaxSize 10
typedef struct Node{ElemType data;int next;
}SLinkList[MaxSize];void testSLinkList(){SLinkList a;
}
静态链表:用数组的方式实现的链表
优点:增、删操作不需要大量移动元素
缺点:不能随机存取,只能从头结点开始依次往后查找;容量固定不可变
2.3.6顺序表和链表的比较
逻辑结构:
都属于线性表,都是线性结构
存储结构比较:
顺序表:
优点:支持随机存取、存储密度高
缺点:大片连续空间分配不方便,改变容量不方便
链表:
优点:离散的小空间分配方便,改变容量方便
缺点:不可随机存取,存储密度低
基本操作(创销、增删改查):
顺序表:
创建
需要预分配大片连续空间。
若分配空间过小,则之后不方便拓展容量;
若分配空间过大,则浪费内存资源
静态分配:静态数组实现,容量不可改变
动态分配:动态数组(malloc、free)实现,容量可以改变但需要移动大量元素,时间代价高
销毁
修改Length = 0
静态分配:静态数组,系统自动回收空间
动态分配:动态数组(malloc、free),需要手动free
增删
插入/删除元素要将后续元素都后移/前移
时间复杂度O(n),时间开销主要来自移动元素
若数据元素很大,则移动的时间代价很高
查
按位查找:O(1)O(1)O(1)
按值查找:O(nO(nO(n)若表内元素有序,可在O(log2nO(log_2nO(log2n)时间内找到
链表:
创建
只需分配一个头结点(也可以不要头结点,只声明一个头指针),之后方便拓展
销
依次删除各个结点(free)
增删
插入/删除元素只需修改指针即可
时间复杂度O(n),时间开销主要来自查找目标元素
查找元素的时间代价更低
查
按位查找:O(n)O(n)O(n)
按值查找:O(n)O(n)O(n)
用哪个:
表长难以预估、经常要增加/删除元素——链表
表长可预估、查询(搜索)操作较多——顺序表
