当前位置：首页 > news >正文

复矩阵与共轭转置矩阵乘积及其平方根矩阵

news 2025/7/26 8:30:01

设 $\mathbf{A}$ 是一个 $\mathbf{m \times n}$ 的复数矩阵，其共轭转置矩阵（Hermitian 共轭）记为 $\mathbf{A^*}$ （即 $\mathbf{A^{^*} = \overline{A}^T}$ ），则矩阵 $\mathbf{P = A A^{^*}}$ （ $\mathbf{m \times m}$ ）和 $\mathbf{Q = A^{^*} A}$ （ $\mathbf{n \times n}$ ）的性质如下文所述。

1. Hermitian 性（自共轭性）

$\mathbf{P}$ 和 $\mathbf{Q}$ 都是 Hermitian 矩阵，即：

$\mathbf{P^* = (A A^{^*})^{^*} = A^{^{**}} A^{^*} = A A^{^*} = P}$

同理 $\mathbf{Q^{^*} = Q}$ 。
这意味着它们的特征值都是实数。

2. 半正定性（Positive Semi-definiteness）

对于任意非零向量 $\mathbf{x} \in \mathbb{C}^m$ ，有：

$\mathbf{x}^* P \mathbf{x} = \mathbf{x}^* A A^* \mathbf{x} = \| A^* \mathbf{x} \|^2 \geq 0$

因此， $\mathbf{P = A A^{^*}}$ 是半正定矩阵（所有特征值 $\geq 0$ ）。同理 $\mathbf{Q = A^{^*} A}$ 也是半正定的。

3. 秩的关系

$\text{rank}(P) = \text{rank}(Q) = \text{rank}(A)$
即 $P$ 和 $Q$ 的秩等于 $A$ 的秩。

4. 特征值的非负性

由于 $P$ 和 $Q$ 是半正定的，它们的特征值都是非负实数。此外：

$P$ 的非零特征值与 $Q$ 的非零特征值相同（尽管维数可能不同）。

如果 $A$ 是方阵且可逆，则 $P$ 和 $Q$ 是正定矩阵（所有特征值 $> 0$ ）。

5. 矩阵 $P = A A^{^*}$ 开平方根

5.1 存在平方根矩阵

首先， $P = A A^{^*}$ 时， $P$ 可以开平方根！
因为 $P$ 是半正定 Hermitian 矩阵，它一定存在唯一的半正定平方根 $\sqrt{P}$ ，

即：

$\sqrt{P} \cdot \sqrt{P} = P = A A^{^*}$

5.2 计算方法

5.2.1. 谱分解（对角化）

由于 $P$ 是 Hermitian 矩阵，它可以被对角化为：

$\mathbf{P = U D U^{^*}}$

其中 $U$ 是酉矩阵（ $U U^* = I$ ）， $D$ 是对角矩阵，其对角元素是 $P$ 的特征值（非负实数）。
则平方根为：

$\sqrt{P} = U \sqrt{D} U^*$

其中 $\sqrt{D}$ 是对 $D$ 的对角元素取算术平方根。

5.2.2. Cholesky 分解（如果 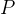$P$ 正定）

如果 $P$ 是正定的（即 $A$ 是满秩的），还可以计算 Cholesky 分解：

$P = L L^*$

其中 $L$ 是下三角矩阵，此时 $\sqrt{P}$ 可以取 $L$ 。

综上， $P = A A^{^*}$ 是半正定 Hermitian 矩阵，其特征值非负，可以开平方根。

平方根 $\sqrt{P}$ 存在且唯一（如果要求半正定），可以通过谱分解或 Cholesky 分解计算。

如果 $A$ 是方阵且可逆，则 $P$ 是正定的，平方根计算更简单。

5.3 共轭转置矩阵乘积平方根的常见应用场景

在量子力学中，密度矩阵 $\rho$ 满足 $\rho = \rho^*$ 且半正定，可以定义 $\sqrt{\rho}$ 。在信号处理和统计学中，协方差矩阵 $\Sigma$ 是半正定的，其平方根用于白化变换。在奇异值分解（SVD）中， $A A^*$ 和 $A^* A$ 的平方根与 $A$ 的奇异值直接相关。