当前位置： 首页 > news >正文

Faiss中L2欧式距离与余弦相似度：究竟该如何选择？

news 2025/7/28 11:32:45

文章概要
作为一名从事向量搜索和推荐系统开发的工程师，我经常被Faiss中L2距离和余弦相似度的选择问题所困扰。本文将深入剖析这两种距离度量方式在Faiss中的实现原理、本质区别以及各自适用的应用场景，帮助你做出更合适的技术选型。

你有没有遇到过这样的场景：在做向量检索的时候，信心满满地选了“最常用”的L2距离，结果上线后发现效果差强人意？或者听说别人用余弦相似度效果更好，却不知道怎么在Faiss里“正确打开”？别急，今天我们就来揭开Faiss中距离度量的神秘面纱，让你不再“瞎选”，而是“选得明白，用得放心”！

Faiss，这个由Facebook AI出品的向量搜索神器，默认可不是“啥都给你打包好”的懒人模式。它默认支持的距离类型主要有两种：

  • L2 距离（欧氏距离）：也就是我们常说的“两点之间的直线距离”。
  • 内积（Inner Product）：向量点乘，听起来有点抽象，但其实它是实现余弦相似度的“幕后功臣”。

默认情况下，Faiss使用的是 L2 距离，比如你初始化一个 IndexFlatL2，它就会用欧氏距离来找最近邻。但注意了，这并不意味着它天生就适合你所有的任务。选错了，就像穿反了鞋子，走不远还累得慌。

L2距离的计算方式非常直观：

L2(x,y)=∑i=1n(xi−yi)2 \text{L2}(x, y) = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2} L2(x,y)=i=1∑n​(xi​−yi​)2​

简单来说，就是两个向量在空间中“飞”过去要走的直线距离。Faiss中通过 IndexFlatL2 或者 METRIC_L2 来实现。

优点：直观、易理解，适合对向量幅值敏感的场景，比如图像特征检索。

内积的计算方式是：

Inner Product(x,y)=∑i=1nxi⋅yi \text{Inner Product}(x, y) = \sum_{i=1}^{n} x_i \cdot y_i Inner Product(x,y)=i=1∑n​xi​⋅yi​

看起来简单粗暴，但它其实藏着玄机。内积的结果大小不仅和向量方向有关，还和向量的长度（模）有关。换句话说，两个向量即使方向一致，但如果一个“个子高”，内积也会更大。

在Faiss中，你可以通过 IndexFlatIP 或设置 METRIC_INNER_PRODUCT 来使用内积。但注意，它不是直接等于余弦相似度，除非你对向量做了归一化！

说到余弦相似度，很多人第一反应是：“这不是应该直接支持吗？”但Faiss偏偏不按常理出牌，它不直接提供余弦相似度，而是让你通过内积 + 向量归一化来“曲线救国”。

余弦相似度公式：

Cosine Similarity(x,y)=x⋅y∣∣x∣∣⋅∣∣y∣∣ \text{Cosine Similarity}(x, y) = \frac{x \cdot y}{||x|| \cdot ||y||} Cosine Similarity(x,y)=∣∣x∣∣⋅∣∣y∣∣x⋅y​

而如果你对两个向量都做了L2归一化（即让每个向量的模长为1），那么分母就变成了1，此时：

Cosine Similarity(x,y)=x⋅y \text{Cosine Similarity}(x, y) = x \cdot y Cosine Similarity(x,y)=x⋅y

也就是说，归一化后的内积 = 余弦相似度！

所以在Faiss中，要实现余弦相似度，你需要：

  1. 使用 METRIC_INNER_PRODUCT（或 IndexFlatIP）
  2. 对输入向量进行L2归一化（faiss.normalize_L2()）

这就像你去吃火锅，锅底是内积，调料是归一化，搭配起来才能调出“余弦相似度”的好味道。

所以，Faiss的距离度量世界，并不是非黑即白，而是像调酒一样，讲究“配方”。搞清楚这些基础概念，才能在后续的选型中游刃有余，不再“靠猜”。接下来，我们就来深入对比一下L2和余弦相似度的本质区别，看看它们到底谁更适合你的任务。

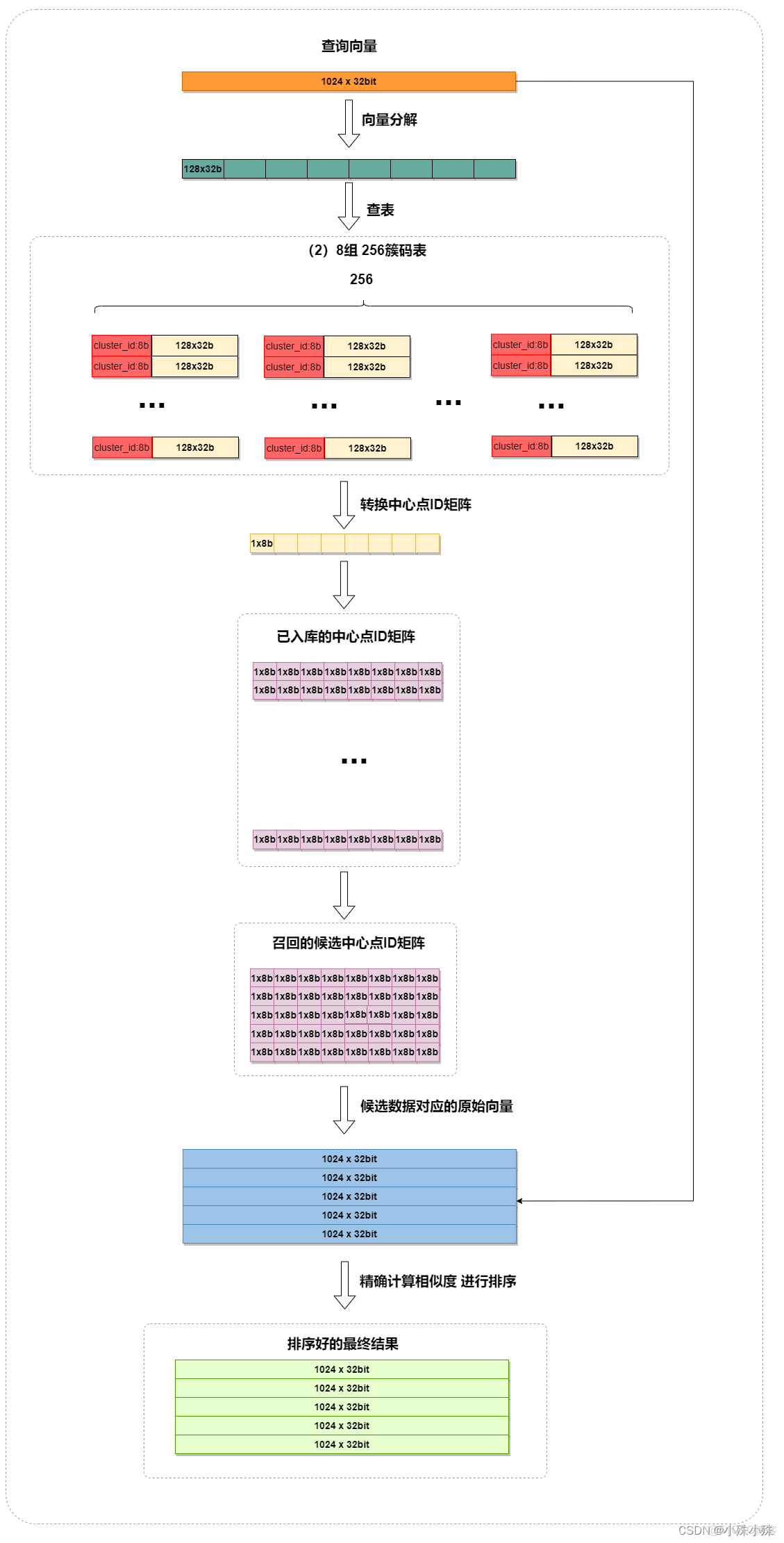
L2欧式距离与余弦相似度的本质区别

在Faiss中，L2欧式距离和余弦相似度是两种最常用的距离度量方式。虽然它们都能衡量向量之间的“相似性”，但其背后的数学原理、应用场景和敏感性却大相径庭。接下来，我们从三个维度深入剖析它们的本质区别。

2.1 数学定义与计算方式对比

首先，我们从数学定义入手，看看这两种度量方式是如何计算的。

L2欧式距离（Euclidean Distance）

L2距离是我们在日常生活中最直观的距离概念，比如两点之间的直线距离。在向量空间中，两个向量 $ A $ 和 $ B $ 的L2距离定义为：

L2(A,B)=∑i=1n(Ai−Bi)2 \text{L2}(A, B) = \sqrt{\sum_{i=1}^{n}(A_i - B_i)^2} L2(A,B)=i=1∑n​(Ai​−Bi​)2​

换句话说，它衡量的是两个向量在空间中的“绝对距离”。

余弦相似度（Cosine Similarity）

余弦相似度则关注的是两个向量之间的“角度”，而不是它们的绝对位置。它的定义如下：

Cosine Similarity(A,B)=A⋅B∣∣A∣∣⋅∣∣B∣∣ \text{Cosine Similarity}(A, B) = \frac{A \cdot B}{||A|| \cdot ||B||} Cosine Similarity(A,B)=∣∣A∣∣⋅∣∣B∣∣A⋅B​

其中，$ A \cdot B $ 是向量点积，$ ||A|| $ 和 $ ||B|| $ 是向量的模长（L2范数）。

关键点：L2距离关注的是“有多远”，而余弦相似度关注的是“方向是否一致”。

2.2 对向量幅值（magnitude）的敏感性分析

这是两者最本质的区别之一。

L2距离：对向量长度非常敏感

举个例子：

  • 向量 $ A = [1, 2] $
  • 向量 $ B = [2, 4] $

这两个向量的方向完全一致，但B是A的两倍长度。此时：

  • L2距离 = $ \sqrt{(1-2)^2 + (2-4)^2} = \sqrt{1+4} = \sqrt{5} \approx 2.24 $
  • 余弦相似度 = 1（完全同向）

结论：L2距离会因为向量长度不同而给出“不相似”的判断，即使它们方向一致。

余弦相似度：忽略幅值，只看方向

继续上面的例子，余弦相似度为1，说明两个向量在方向上完全一致，尽管它们的长度不同。

应用场景提示：如果你关心的是“语义相似”而非“强度相似”，余弦相似度是更好的选择。

2.3 几何意义：距离 vs 角度

从几何角度理解，两者的差异更加直观。

L2距离：衡量空间中的“直线距离”

想象你在地图上找两个地点之间的最短路径，L2距离就是这条直线的长度。它适合那些向量的绝对数值具有实际物理意义的场景，比如图像像素、坐标点等。

余弦相似度：衡量向量之间的“夹角”

它更像是在问：“这两个向量指向的方向是否一致？” 不管它们有多长，只要方向一致，就是“相似”的。

形象比喻：

  • L2距离像是在问：“你离我多远？”
  • 余弦相似度像是在问：“你是不是和我一路人？”

小结一下 🧠

特性L2欧式距离余弦相似度
数学本质向量间的绝对距离向量间的方向一致性
是否关注幅值✅ 是❌ 否
适合场景图像检索、空间数据文本相似度、推荐系统
Faiss实现直接支持通过内积 + L2归一化实现

选择L2还是余弦相似度，不是“哪个更好”的问题，而是“哪个更适合你的数据和任务”的问题。在下一节中，我们将深入探讨如何在Faiss中正确实现余弦相似度搜索。

Faiss中实现余弦相似度的正确方法

在Faiss中，虽然没有直接支持余弦相似度的索引类型，但聪明的工程师们早已找到了“曲线救国”的妙招——通过内积（Inner Product）+ L2归一化的方式，完美模拟余弦相似度的行为。接下来，我们就来一步步拆解这个“魔法”操作，让你在Faiss中也能优雅地使用余弦相似度。

3.1 使用内积（METRIC_INNER_PRODUCT）的前提条件

Faiss默认使用的是L2欧式距离（比如IndexFlatL2），但如果你想实现余弦相似度，就得换一种玩法：使用内积索引，也就是IndexFlatIP（Inner Product）。

不过，这里有个非常关键的前提条件：

只有当向量已经经过L2归一化后，内积才等价于余弦相似度。

换句话说，如果你直接把原始向量扔进IndexFlatIP里，那得到的结果并不是你想要的余弦相似度，而是一个“混杂了长度和角度”的奇怪值。

所以，使用内积的前提是：

✅ 所有向量必须先进行L2归一化处理。

在Faiss中创建一个支持内积的索引，可以这样写：

import faiss
import numpy as npdim = 128  # 向量维度
index = faiss.IndexFlatIP(dim)  # 使用内积 IndexFlatIP

记住：先归一化，再插入数据！

3.2 向量L2归一化的必要性与实现

为什么一定要做L2归一化？因为余弦相似度本质上只关心两个向量之间的夹角，而不在乎它们的长度（幅值）。L2归一化的作用，就是把每个向量的长度统一缩放为1，这样内积的结果就只反映夹角信息了。

✅ L2归一化的数学表达：

对于向量 $ x $，其L2归一化为：
x^=x∥x∥2 \hat{x} = \frac{x}{\|x\|_2} x^=∥x∥2​x​

在Python中，Faiss贴心地提供了内置的归一化函数：

from faiss import normalize_L2vectors = np.random.rand(1000, 128).astype('float32')  # 假设有1000个128维向量
normalize_L2(vectors)  # 原地归一化

你也可以使用sklearn来实现归一化：

from sklearn.preprocessing import normalizevectors_normalized = normalize(vectors, norm='l2', axis=1)

⚠️ 注意：不仅是训练数据要归一化，查询向量也必须归一化，否则结果会失真！

3.3 与sklearn等工具库结果的一致性验证

为了验证Faiss中使用内积+归一化是否真的等价于余弦相似度，我们可以拿sklearn的cosine_similarity做个对比实验，看看两者是否“英雄所见略同”。

🧪 示例代码：
from sklearn.metrics.pairwise import cosine_similarity
import faiss
import numpy as np
from faiss import normalize_L2# 构造测试数据
np.random.seed(42)
vectors = np.random.rand(5, 128).astype('float32')# 归一化
normalize_L2(vectors)# 使用Faiss计算内积相似度
index = faiss.IndexFlatIP(128)
index.add(vectors)
distances, indices = index.search(vectors[:1], 5)# 使用sklearn计算余弦相似度
sim_sklearn = cosine_similarity(vectors[:1], vectors)print("Faiss内积结果：", distances)
print("Sklearn余弦相似度：", sim_sklearn)

运行后你会发现，两者结果几乎完全一致（误差在浮点精度范围内）！

✅ 结论：在Faiss中实现余弦相似度的关键步骤是：

  1. 使用IndexFlatIP（内积索引）
  2. 对所有向量进行L2归一化
  3. 查询时也对查询向量做归一化

掌握了这些，你就不会再被“Faiss不支持余弦相似度”的说法误导啦！下次在做文本相似度、推荐系统时，就可以放心大胆地用Faiss来实现余弦相似度了。

应用场景分析与选型建议

在Faiss中，L2欧式距离和余弦相似度虽然都能用于衡量向量之间的相似性，但它们的适用场景却大相径庭。选择哪种方式，不仅要看数据本身的特性，还要结合业务目标。接下来，我们就来聊聊在实际应用中，如何根据场景做出更明智的选择。

4.1 推荐系统与文本相似度：为何偏爱余弦相似度？

在推荐系统和文本相似度计算中，余弦相似度往往是首选。

为什么？

因为这类任务更关注向量的方向，而不是它们的长度。举个例子：

假设你有两个用户，一个用户只看过几部电影，另一个用户看过成百上千部。他们的观影向量在数值上可能差异巨大，但方向却可能非常接近——这意味着他们的兴趣相似。

在这种情况下，如果使用L2距离，由于向量长度不同，系统可能会误判这两个用户“不相似”。而余弦相似度只看夹角，能更准确地反映用户的兴趣匹配程度。

实际应用中的优势：
  • 忽略向量幅值：对文本向量来说，向量长度往往代表词频或文档长度，而我们更关心的是语义方向。
  • 适用于高维稀疏向量：如TF-IDF、Word2Vec等生成的向量，更适合用余弦相似度衡量。

所以，在推荐系统、语义搜索、NLP任务中，余弦相似度是更稳健的选择。

4.2 图像检索与空间数据：L2距离的优势所在

与推荐系统不同，图像检索、空间数据匹配等任务则更倾向于使用L2欧式距离。

为什么？

因为这些场景中，向量的每个维度往往代表某种空间位置或像素值，向量的绝对距离就变得非常重要。

实际应用中的优势：
  • 保留空间信息：比如在图像特征匹配中，两个图像的特征向量如果在空间上接近，说明它们在视觉上也更相似。
  • 对向量幅值敏感：在图像、音频等密集向量中，向量长度本身就携带了重要信息，L2距离能更好地捕捉这些细节。
举个例子：

如果你正在做一个图像搜索引擎，用户上传一张猫的照片，你想找到视觉上最接近的图片，那么L2距离会更合适，因为它能精确衡量像素级别的差异。

因此，在图像识别、视觉搜索、地理空间检索等任务中，L2欧式距离是更自然的选择。

4.3 实际项目中Faiss配置的修改方法（如langchain集成）

在实际项目中，尤其是使用像Langchain这样的框架时，默认的Faiss配置可能并不符合你的需求。比如，默认使用的是L2距离，但你可能需要余弦相似度。

如何修改Faiss配置？

以Langchain为例，Faiss默认使用的是IndexFlatL2，即基于L2距离的索引。若要切换为余弦相似度，你需要：

步骤一：修改索引类型为内积（METRIC_INNER_PRODUCT）
import faiss
# 假设你的向量维度是768
dimension = 768
index = faiss.IndexFlatIP(dimension)  # 使用内积代替L2
步骤二：对向量做L2归一化
from faiss import normalize_L2
import numpy as npvectors = np.array(your_vectors).astype('float32')
normalize_L2(vectors)  # 归一化向量
步骤三：构建Faiss索引并添加向量
index.add(vectors)

这样，Faiss就会以余弦相似度的方式进行向量匹配。

小贴士：
  • 在Langchain中，你可以通过修改faiss.py中的索引初始化部分来实现全局替换。
  • 如果你使用的是HuggingFace Embeddings，记得在归一化前确认向量是否已经标准化。

总结一下：

场景推荐距离度量原因
推荐系统、文本相似度余弦相似度忽略向量长度，关注方向
图像检索、空间数据L2欧式距离捕捉空间位置差异
Langchain等项目集成内积 + L2归一化实现余弦相似度匹配

选对距离度量，才能让Faiss发挥最大威力。
别再盲目使用默认配置了，理解你的数据，才能做出更聪明的技术决策！

http://www.dtcms.com/a/295213.html

相关文章：

  • Web前端入门：JavaScript 哪些地方需要 try...catch 异常捕获
  • 【图论】倍增与lca
  • Avalonia 基于MVVM的时间统计/系统时间显示 示例
  • EPSON爱普生全系列废墨垫已满清零工具分享附教程下载
  • EasyExcel 模板导出数据 + 自定义策略（合并单元格）
  • 基于深度学习的胸部 X 光图像肺炎分类系统（三）
  • Turbo Intruder 并发插件无法试用--更换新版Burpsuit解决（简单解决安装、破解问题）
  • 开源Qwen凌晨暴击闭源Claude！刷新AI编程SOTA，支持1M上下文
  • 跨境支付入门～国际支付结算（结算篇）
  • AtCoder Beginner Contest 415(ABCDE)
  • `neutron router-gateway-set` 操作失败的可能原因及解决方案
  • 深度分析Java多线程机制
  • 【智能协同云图库】智能协同云图库第六弹：空间模块开发
  • 微服务的编程测评系统6-管理员登录前端-前端路由优化
  • 【开源】WPF的数据可视化大屏解决方案——WpfMap
  • 洛谷 P11378 [GESP202412 七级] 燃烧-普及/提高-
  • fdbus4.2 timer的使用
  • AI时代，我的编程工作搭子
  • ospf单区域实验
  • Windows批量工具，直接起飞！
  • 外部存档（External Archive）机制
  • MNIST 手写数字识别模型分析
  • 无人机电池通讯接口应用：CANFD工业级芯片的选型与技术要点
  • 跨境支付入门～国际支付结算（稳定币）
  • 事务的特性 - ACID
  • 游戏装备被盗，运营商赔不赔
  • 算法牢笼与思想飞地：在人工智能时代守卫灵魂的疆域
  • gig-gitignore工具实战开发（二）：设计多源模板系统
  • Python--Tkinter--标准 GUI 工具包
  • 常用的Typescript特性