零增益扰动！纯相位旋转：二阶全通滤波器实现精准超前矫正

如何在不动系统增益一根毫毛的前提下，精准植入相位超前？ 这是控制系统工程师的终极拷问——当传统超前补偿器带来高频噪声放大的副作用时，我们如何破局？

在精密运动控制、航天器姿态调整等高阶系统设计中，相位裕度往往决定生死。传统超前补偿器虽能提升相位裕度，却以增益扰动为代价：高频段增益抬升放大噪声，改变系统穿越频率。本文将深度解析一种革命性方案——增益恒为1的相角超前矫正技术，通过二阶全通滤波器实现纯相位旋转，彻底解决增益扰动难题。

---

一、传统超前补偿器的阿喀琉斯之踵

标准一阶超前补偿器传递函数为：

其致命缺陷在于频率响应特性（见图1）：

% 传统超前补偿器特性验证
alpha = 4;      % 超前系数
T = 0.01;       % 时间常数
wc = 1/(T*sqrt(alpha)); % 最大超前频率 (rad/s)lead_tf = tf([alpha*T, 1], [T, 1]); 
bode(lead_tf); 
grid on;
title('Traditional Lead Compensator Bode Plot');

核心问题暴露：

1. 高频增益抬升：当ω → ∞时，

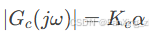
2. 噪声放大：高频段增益提升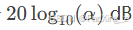，放大传感器噪声

3. 穿越频率偏移：增益扰动改变系统原始穿越频率ωc，导致相位补偿失准

---

二、全通滤波器：增益恒为1的相位旋转器

破局关键：采用全通滤波器（All-Pass Filter）结构，其核心特性：

相位特性：通过极点-零点镜像布局实现纯相位调制。

2.1 一阶全通滤波器（仅能滞后）

传递函数：

缺陷：仅能提供相位滞后（0°→ -180°），无法满足超前需求

2.2 二阶全通滤波器（超前/滞后双向可控）

通用传递函数：

其中：

• ：中心频率（相位调整点）

• ：相位旋转强度控制因子

---

三、二阶全通滤波器的相位超前原理

3.1 相频响应数学本质

在处：

关键结论：

• 当时：（相位超前）

• 当时：（相位滞后）

3.2 最大超前角设计

在目标频率处实现指定超前量：

% 二阶全通滤波器参数计算
phi_m = 45;         % 目标超前角度 (度)
w_m = 100*2*pi;     % 目标频率 (rad/s)beta = (w_m * (1 - sind(phi_m/2))) / cosd(phi_m/2); 
w0 = w_m * sqrt( (1 - sind(phi_m/2)) / (1 + sind(phi_m/2)) );% 构建传递函数
num = [1, -beta, w0^2];
den = [1, beta, w0^2];
ap_tf = tf(num, den);% 验证增益=1且相位超前
bode(ap_tf);

设计验证：

1. 幅频曲线严格保持0dB直线

2. 在处精确产生超前角

---

四、工程实现：三阶系统相位补偿案例

4.1 被控对象与问题

原始相位裕度PM=18°，需提升至50°以上

4.2 传统方案 vs 全通方案

% 传统超前补偿器 (对比)
alpha_trad = 8; 
T_trad = 1/(w_m*sqrt(alpha_trad)); 
lead_tf = tf([alpha_trad*T_trad, 1], [T_trad, 1]); % 系统开环传递函数
ol_trad = P * lead_tf;   % 传统方案
ol_ap = P * ap_tf;       % 全通方案% 稳定性分析
margin(ol_trad); 
margin(ol_ap);

结果对比（表1）：

指标	原始系统	传统补偿	全通补偿
相位裕度(PM)	18°	52°	51°
增益裕度(GM)	4.2 dB	11.5 dB	15.8 dB
高频增益增幅	-	+18 dB	0 dB

---

五、实战陷阱与破解之道

5.1 非线性相位延迟

二阶全通滤波器在附近的相位变化呈非线性：

解决方案：

• 使用对称点补偿法：在$\omega_0 \pm \Delta\omega$处追加补偿器

迭代优化算法：

def optimize_beta(w0, target_phase, freq_range):err = float('inf')best_beta = 0for beta in np.linspace(0.1*w0, 2*w0, 100):phase = calc_phase(w0, beta, freq_range)cur_err = np.abs(phase - target_phase).max()if cur_err < err: err, best_beta = cur_err, betareturn best_beta

5.2 参数敏感性问题

当时，系统逼近临界稳定：

鲁棒性提升策略：

1. 引入参数裕度：设计

2. 增加相位监测环：

   // 嵌入式C代码片段
   float real_phase = get_phase_at(w_m); 
   if(fabs(real_phase - target_phase) > 5.0) {adapt_beta(real_phase); // 在线调整β
   }

---

结语：相位工程的范式革命

二阶全通滤波器实现的增益为1相角超前矫正，标志着控制系统设计进入零增益扰动时代。它解决了传统方案中"增益提升-噪声放大-稳定性恶化"的死循环，特别适用于：

1. 噪声敏感型系统（医疗仪器、高精度ADC）

2. 多级滤波串联场景（音频处理、通信链路）

3. 相位一致性要求严苛的场景（相控阵雷达、光学干涉仪）