【每日算法】专题十八_BFS 解决拓扑排序

1. 算法思想

BFS 解决拓扑排序（Topological Sort）的核心思想是基于节点的入度（In-degree）进行层次遍历，确保每个节点在其所有前驱节点被处理后才被访问。这种方法也称为Kahn 算法，具体步骤如下：

算法思想

1. 构建图与入度数组
   将问题抽象为有向图，统计每个节点的入度（即有多少条边指向该节点）。入度为 0 的节点表示没有前驱，可以作为起点。

2. 初始化队列
   将所有入度为 0 的节点加入队列。这些节点是拓扑排序的起点。

3. BFS 处理节点

   • 取出队首节点：每次从队列中取出一个节点，并将其加入结果序列。
   • 更新邻接节点的入度：遍历该节点的所有后继节点，将它们的入度减 1。
   • 入度为 0 的节点入队：若某个后继节点的入度变为 0，说明其所有前驱节点已被处理，将其加入队列。

4. 环检测
   若最终结果序列的长度等于图的节点数，则说明图中无环，拓扑排序成功；否则，图中存在环，无法完成排序。

关键点

• 入度的维护：入度数组是核心数据结构，用于动态跟踪节点的依赖关系。
• 队列的层次遍历：BFS 保证了节点按依赖关系的层次顺序被处理。
• 环检测原理：若存在环，环中的节点入度始终无法变为 0，导致最终结果序列长度不足。

复杂度分析

• 时间复杂度：O (V + E)，其中 V 是节点数，E 是边数。
• 空间复杂度：O (V + E)，主要用于存储邻接表和入度数组。

应用场景

• 课程表安排（课程依赖关系）
• 项目任务调度（任务先后顺序）
• 编译依赖解析（文件编译顺序）
• 外星词典序问题（如用户最初的问题）

这种方法通过入度数组和 BFS 队列巧妙地解决了拓扑排序问题，是处理有向无环图（DAG）依赖关系的经典算法。

2. 例题

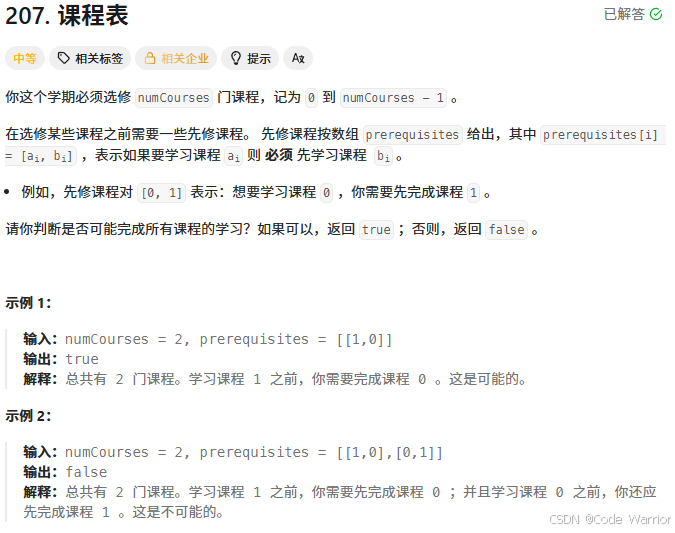
2.1 课程表

207. 课程表 - 力扣（LeetCode）

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {// 把所有入度为0的点加入到队列中// 邻接表存图unordered_map<int, vector<int>> edge;// 标记每一个定义的入度vector<int> in(numCourses);for(auto e : prerequisites){int a = e[0], b = e[1]; // b -> aedge[b].push_back(a);++in[a];}// 将所有入度为0的点入队列queue<int> q;for(int i = 0; i < numCourses; ++i){if(!in[i]) q.push(i);}while(q.size()){int tmp = q.front(); q.pop();for(auto e : edge[tmp])if(!(--in[e])) q.push(e); // 入度为0的入进去}for(int i = 0; i < numCourses; ++i){if(in[i]) return false;}return true;}
};

2.2 课程表 II

210. 课程表 II - 力扣（LeetCode）

class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {// 邻接表存图unordered_map<int, vector<int>> edge;// 入度vector<int> in(numCourses);for(auto e : prerequisites){int a = e[0], b = e[1]; // b->aedge[b].push_back(a);++in[a];}queue<int> q;for(int i = 0; i < numCourses; ++i){if(!in[i]) q.push(i);}vector<int> ret;while(q.size()){int t = q.front(); q.pop();ret.push_back(t);for(auto e : edge[t])if(!(--in[e])) q.push(e);}if(ret.size() != numCourses) return {};return ret;}
};

2.3 火星词典

LCR 114. 火星词典 - 力扣（LeetCode）

核心思路是通过构建有向无环图（DAG）并进行拓扑排序来确定外星语言的字母顺序。以下是具体步骤的说明：

1. 初始化数据结构：使用邻接表edges存储字母间的依赖关系，使用入度表in记录每个字母的入度。

2. 构建图：

   • 遍历输入的单词列表，为每个出现的字母初始化入度为 0。
   • 比较每对相邻单词，找到第一个不同的字符，建立从前者到后者的有向边，并更新后者的入度。
   • 特殊情况处理：如果一个单词是另一个的前缀且更长，说明顺序矛盾，标记cheak为真。

3. 拓扑排序：

   • 将所有入度为 0 的字母加入队列。
   • 每次从队列取出一个字母，将其加入结果字符串，并减少其所有邻接字母的入度。若邻接字母入度变为 0，则加入队列。
   • 检查最终结果：若所有字母的入度都被减为 0，说明存在有效的字母顺序；否则返回空字符串。

4. 矛盾检测：在构建图的过程中，如果发现前一个单词是后一个单词的前缀但更长（如abc和ab），直接返回空字符串。

通过这种方法，代码能够根据给定的单词列表推断出外星语言的字母顺序，或者判断是否存在矛盾导致无法确定顺序。

 

class Solution {
public:// 邻接表存图unordered_map<char, unordered_set<char>> edges;// 记录入度unordered_map<char, int> in;bool cheak = false;string alienOrder(vector<string>& words) {// 创建一个有向无环图// 拓扑排序// 入度初始化for(auto str : words){for(auto ch : str)in[ch] = 0;}int n = words.size();for(int i = 0; i < n; ++i){for(int j = i + 1; j < n; ++j){add(words[i], words[j]);if(cheak) return "";} }queue<char> q;// 所有的零度入队列for(auto [a, b] : in){if(b == 0) q.push(a);}string ret;while(q.size()){char t = q.front(); q.pop();ret += t;for(auto ch : edges[t]){if(!(--in[ch])) // 零度入队列q.push(ch);}}for(auto [a, b] : in){if(b != 0) return "";}return ret;}void add(string s1, string s2){int n = min(s1.size(), s2.size());int i = 0;for(; i < n; ++i){if(s1[i] != s2[i]) {int a = s1[i], b = s2[i];if(!edges.count(a) || !edges[a].count(b)) // 没有邻接表的才进{edges[s1[i]].insert(s2[i]);++in[s2[i]];}return;}}if(i == s2.size() && i < s1.size()) cheak = true;}
};