强化学习理论

强化学习算法概述

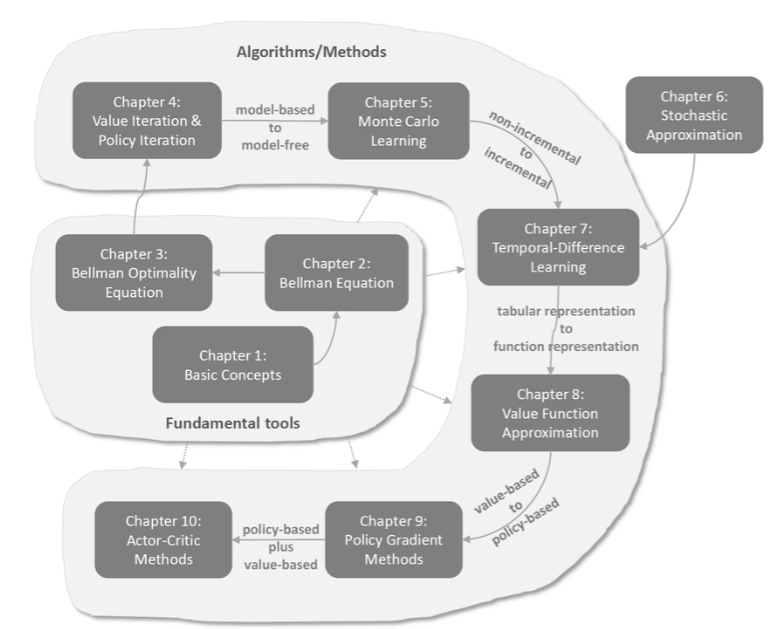
chapter 1：基本概念

chapter2：贝尔曼公式
状态值：从一个状态出发，沿着一个策略所得到奖励回报的平均值，状态值越高说明策略越好
贝尔曼公式：描述了所有状态和状态值的关系，通过公式可以求解出给定策略的状态值，因此能够评价策略好不好（Policy evaluation策略评价）
$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$
chapter3：贝尔曼最优公式
贝尔曼最优公式是贝尔曼公式的特殊情况
强化学习的最终目标是求解最优策略
最优策略：能够得到最大的状态值
分析下面公式使用：不动点原理

1. 求解的最优策略是否存在
2. 给出求解贝尔曼最优公式的策略
   $$v=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }v)=f(v)$$

chapter4：第一批求解的算法
第一批能够求解最优策略的三个算法
Value iteration（值迭代）
Policy iteration（策略迭代）
Truncated policy iteration（上面两个的统一的表示）

每个策略有两个步骤：

1. Policy update
2. Value update
   先进行测量评价，通过评价的值改进策略，反复迭代

chapter5：蒙特卡洛方法（最简单的不需要模型就能找到最优策略的方法）
学习随机变量的期望值（state value和action value全都是随机变量的期望值）
Xi是随机值（没有模型要有数据，没有数据要有模型）
$$\mathbb{E}[X]\approx \bar{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$
效率特别低，现实中并不使用
具体的三个算法

chapter6：随机近似理论
第六章之前是non-incremental，第七章开始是incremental，第六章是过度
non-incremental：一次使用很多采样，所有数据收集完之后一次求平均，得到一个E(x)的近似
incremental：开始时有一个估计，每得到一个采样就更新一次估计
三个典型算法

1. Robbins-Monro(RM) algorithm
2. Stochastic gradient descent(SGD随即下降)

chapter7：
三种算法：

1. TD 的方法学习state value
2. Sarsa：用TD的方法学习action value
3. Q-learning:用TD学习optimal action value

两种策略
behavior policy：用来生成经验数据
target policy：目标策略，不断进行改进希望target policy能够收敛到最优的策略
on-policy： behavior policy和target policy相同，为on-policy
off-policy： behavior policy和target policy可以不同，为off-policy

chapter8：
第七章和前面的数据都是表格状态的
第八章开始是函数形式

chapter9：
第八章和之前都是value-based（改变策略中的参数值）
第九章开始是policy-based（改变策略）

chapter10：actor-Critic Methods
把policy-based和value-based方法结合起来

chapter 1：基本概念

state： 位置等各种状态信息
state space： 状态空间，所有状态的集合
Action： 在每个状态可以采取的一系列的行为
Action space： 所有Action的集合，不同状态的Action是不同的
state transition： 当采取一个action的时候，agent可以从一个state转变为另一个state，state transition就是这个过程
Forbidden area：
有些区域可以进入，但是进入后会有惩罚（虽然有惩罚，但是更优）
有些状态就不能进入
Tabular representation： 用表格的形式表示state transition，每一行都表示一个状态，每一列表示一个action（只能表示确定性情况）

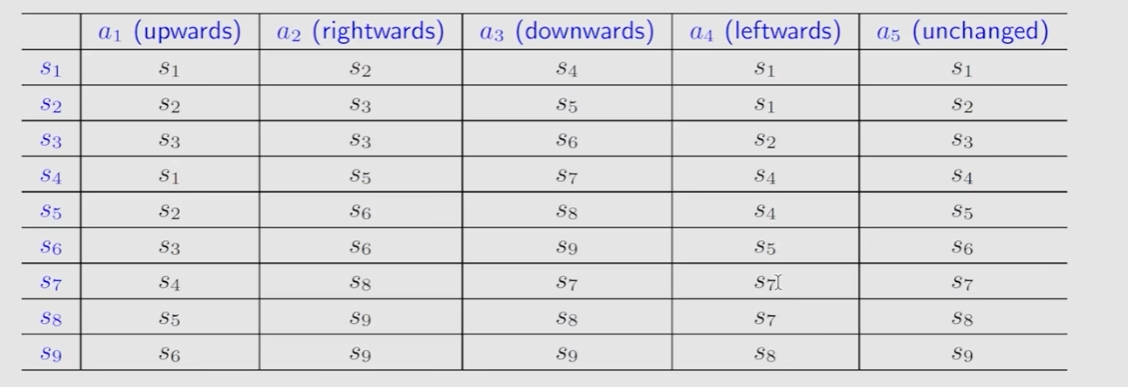
state transition：用语言描述状态，或者用数学表示state transition
policy：告诉agent如果在一个状态下应该采取哪一个action

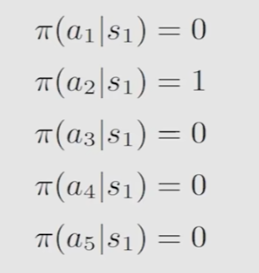
reward：一个数，agent采取action后会得到一个数，这个数为正数表示鼓励这个行为，否则反之
return： 沿着一个路径上的所有rewards加起来

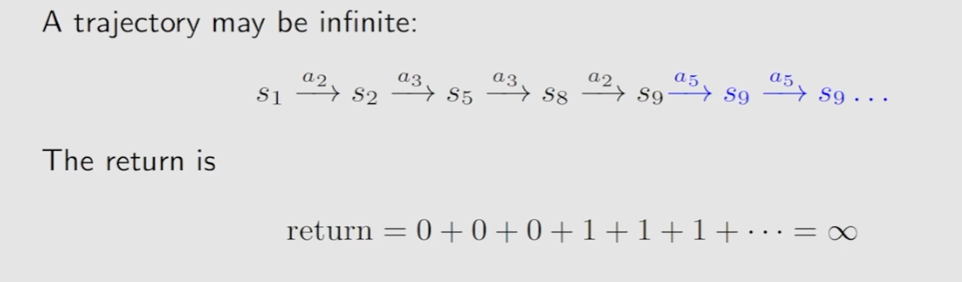
当路径到达终点S9，return仍然会不断增加达到无穷大
引入discount rate解决这个问题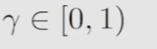

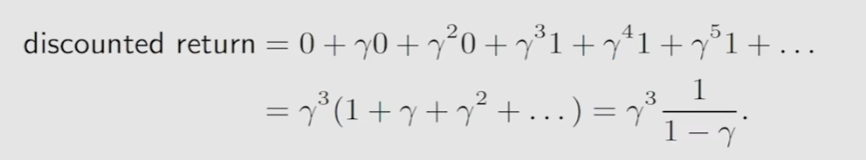
chapter2：贝尔曼公式

Motivating examples（举例计算return）

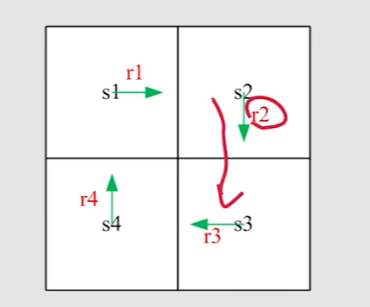
return的计算方法一

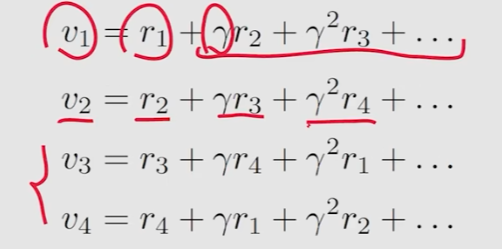
演变为方法二

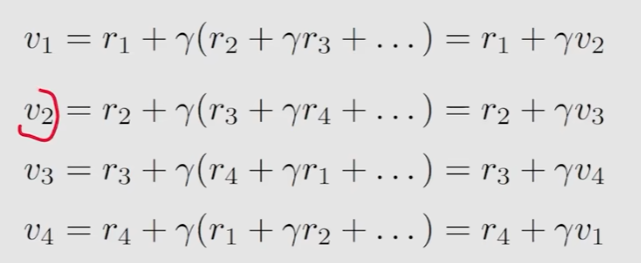
写成矩阵

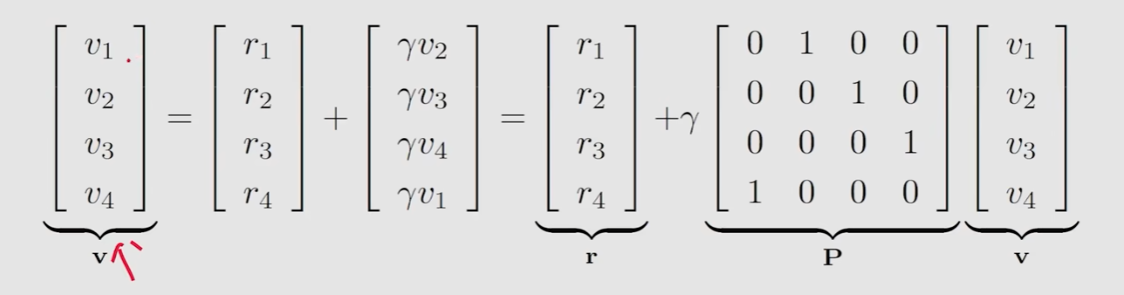
转换成数学公式
$$\mathbf{v}=\mathbf{r}+\gamma \mathbf{Pv}$$

state value

单步执行的数学表示
$$S_t\stackrel{A_t}{\to }{R}_{t+1},S_{t+1}$$
St是当前的状态
At是采取的动作
Rt+1是reward
St+1是执行过的状态
计算discounted return
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$$
state value是Gt的期望值
$$v_{\pi }(s)=\mathbb{E}[G_t|S_t=s]$$

贝尔曼公式推导

计算Gt
$$\begin{array}{rl}{G}_t& =R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots ,\\ & =R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+\dots ),\\ & =R_{t+1}+\gamma G_{t+1},\end{array}$$
计算state value
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[G_t|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & =\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]\end{array}$$
在指定状态s下得到Rt+1的期望
$$\begin{array}{rl}\mathbb{E}[R_{t+1}|S_t=s]& \begin{array}{r}=\sum _a\pi (a|s)\mathbb{E}[R_{t+1}|S_t=s,A_t=a]\end{array}\\ & =\sum _a\pi (a|s)\sum _{r}p(r|s,a)r\end{array}$$
$$\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$$是在指定状态下，发生指定动作，得到的所有可能的结果的期望值
π(a∣s)是在状态s下选择动作a 的概率
$$\begin{array}{rl}\mathbb{E}[G_{t+1}|S_t=s]& \begin{array}{r}=\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]p(s^{\prime }|s)\end{array}\\ & =\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)\end{array}$$
p(s ′ ∣s) 在状态s下采取某个动作转移到s’的概率
E[Gt+1 ∣St =s,St+1 =s ′ ]：从状态s采取某个动作到达s‘所得到的未来Gt+1的值
贝尔曼公式的最终表达式
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s],\\ & \begin{array}{rl}& =\underset{\text{mean of immediate rewards}}{\underbrace{\sum _a\pi (a|s)\sum _{r}p(r|s,a)r}}+\underset{\text{mean of future rewards}}{\underbrace{\gamma \sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime }),}}\end{array}\\ & \begin{array}{r}=\sum _a\pi (a|s)\left[\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })\right],\forall s\in \mathcal{S}.\end{array}\end{array}$$

使用矩阵/向量求解贝尔曼公式

写成矩阵乘法
$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$
案例

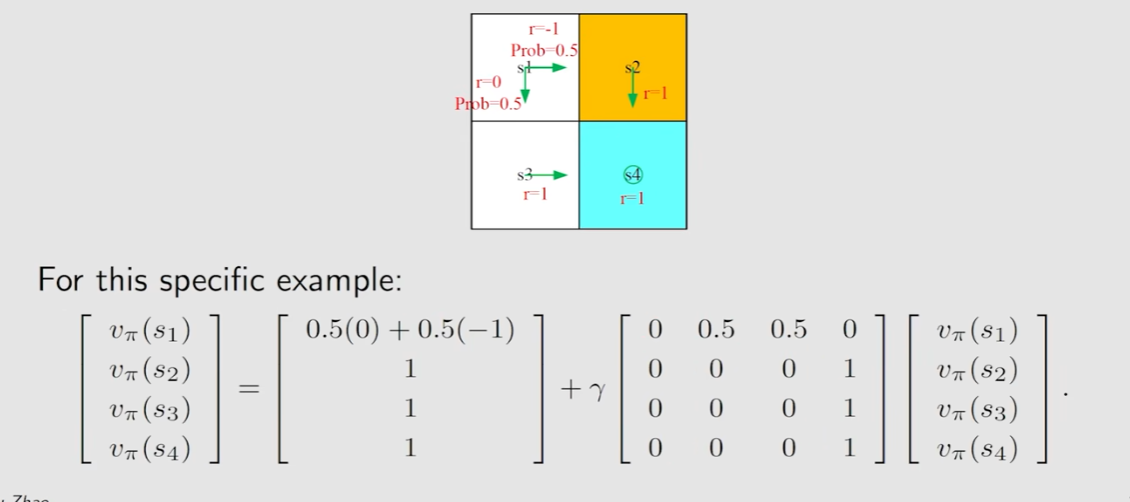
rΠ=r*prob （prob是选择每个r的概率）
pΠ=s到不同位置的prob
贝尔曼公式的迭代过程
$$v_{k+1}=r_{\pi }+\gamma P_{\pi }{v}_k$$
当看趋于无穷大时Vk就hi收敛到VΠ，这个VΠ就是真实的state value

action value

从一个状态出发，采取指定action得到的return的平均值
$$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$$
就是state value中固定了所进行的action
$$q_{\pi }(s,a)=\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })$$

chapter3：贝尔曼最优公式

optimal policy：如果有两个策略，如果在所有状态下，一个策略的state value都大于另一个策略，则说这个策略是更好的
最优策略：如果有一个策略，在所有状态下的state value都优于其他策略，则说这个策略是最好的
贝尔曼公式
$$v(s)=\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in \mathcal{S}$$
贝尔曼最优公式
$$v(s)=\underset{\pi }{\max }\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in \mathcal{S}$$
矩阵格式
$$v=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }v)$$

不动点

当一个点为x，和一个映射关系f，如果f(x)=x, 称这个点为不动点
$$\Vert f(x_1)-f(x_2)\Vert \le \gamma \Vert x_1-x_2\Vert$$

Contraction mapping：一个函数f满足Contraction mapping，则任取两点满足
$$\Vert f(x_1)-f(x_2)\Vert \le \gamma \Vert x_1-x_2\Vert$$

Contraction mapping Theorem：如果一个函数f满足Contraction mapping，对于x=f(x)满足三个结论

1. 一定存在一个x，满足f(x)=x,
2. 上述x是唯一的
3. 可以通过下面这个公式求出x$$x_{k+1}=f(x_k)$$

已知贝尔曼最优公式是满足Contraction mapping Theorem的
可得$$v_{k+1}=f(v_k)=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_k)$$
进而求解
$$v^{\ast }=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$$
最优策略
$${\pi }^{\ast }=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$$
进而得到
$$v^{\ast }=r_{{\pi }^{\ast }}+\gamma P_{{\pi }^{\ast }}{v}^{\ast }$$

chapter4：迭代算法

第四章开始讲算法

值迭代

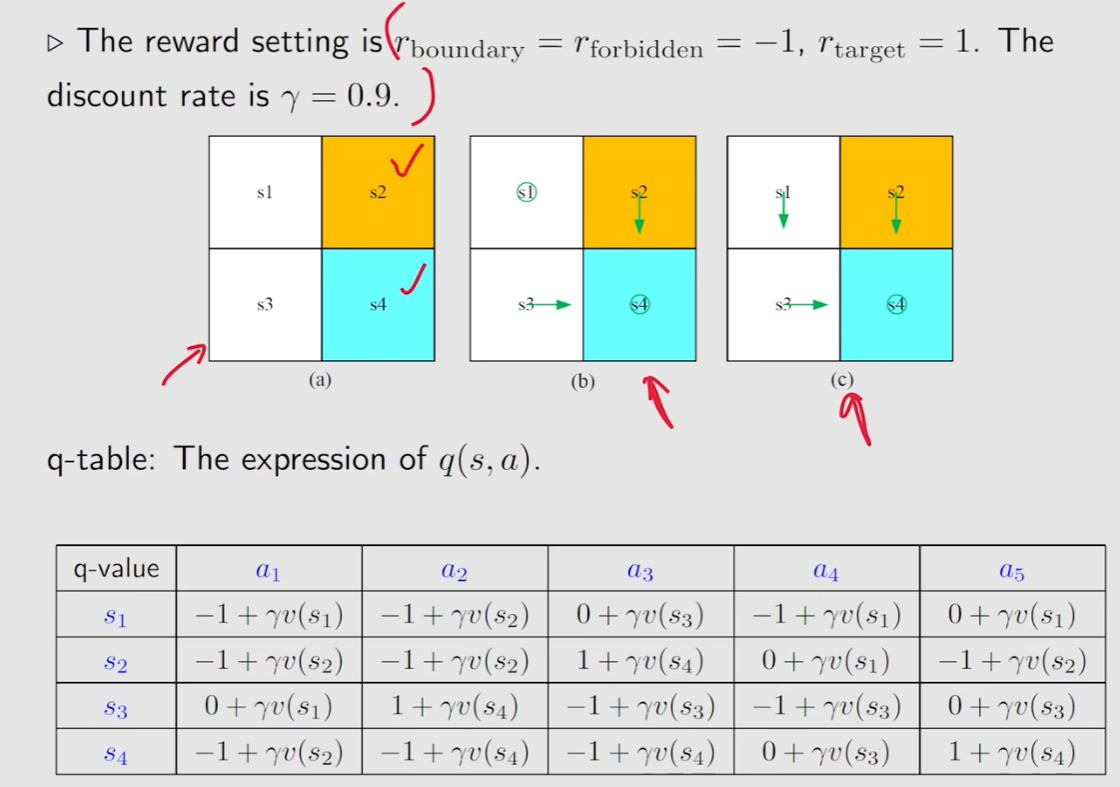
k=0时，选取所有v都是0
Policy update
计算出S1，S2，S3，S4所要做的动作（取计算的最大值）
Value update
V也选最大值

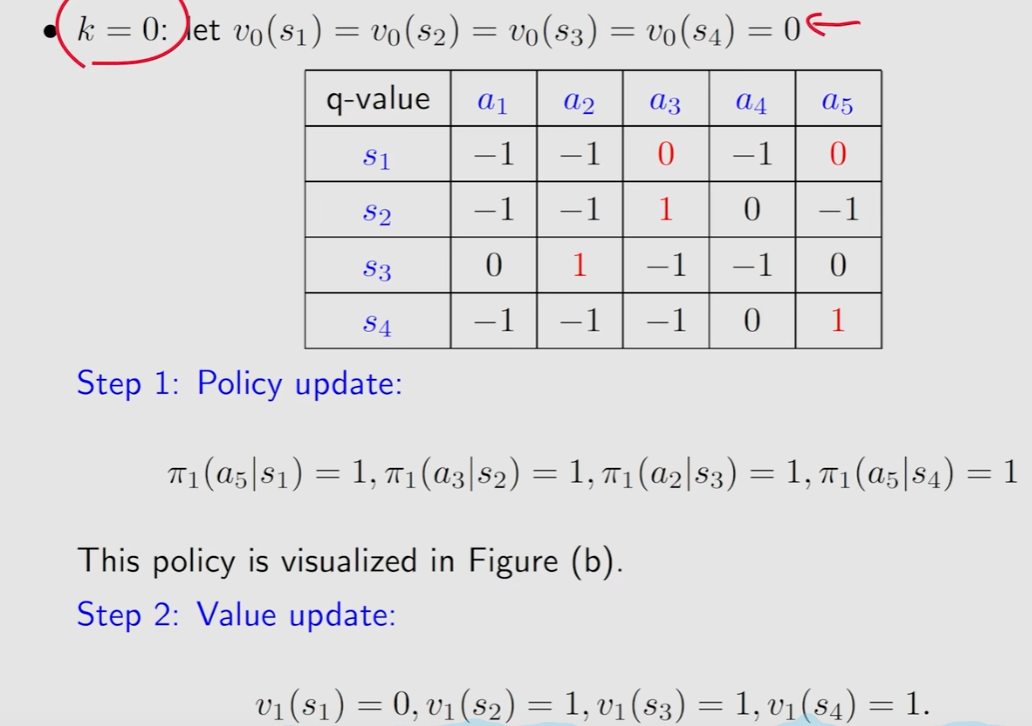
进行迭代计算

当Vk-Vk+1的绝对值很小时就求出来了

策略迭代

给定一个初始策略，在迭代过程中修改策略

1. policy evaluation： 给定一个策略，求解策略对应的贝尔曼公式得到state value的过程
   $$v_{{\pi }_k}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}$$
2. policy improvement： 通过第一步求出的V得到一个新的策略
   $${\pi }_{k+1}^{\ast }=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }\underbrace{v_{{\pi }_k}})$$
   
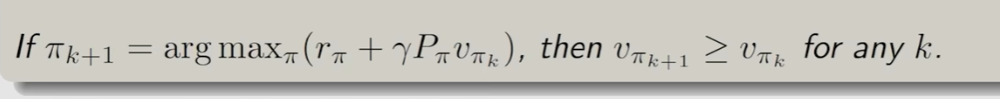
   可以说明迭代的是越来越好的

chapter5：蒙特卡洛方法

model-free方法