一文速通《矩阵的特征值和特征向量》

一、必须记住知识点

(1)

(2) 

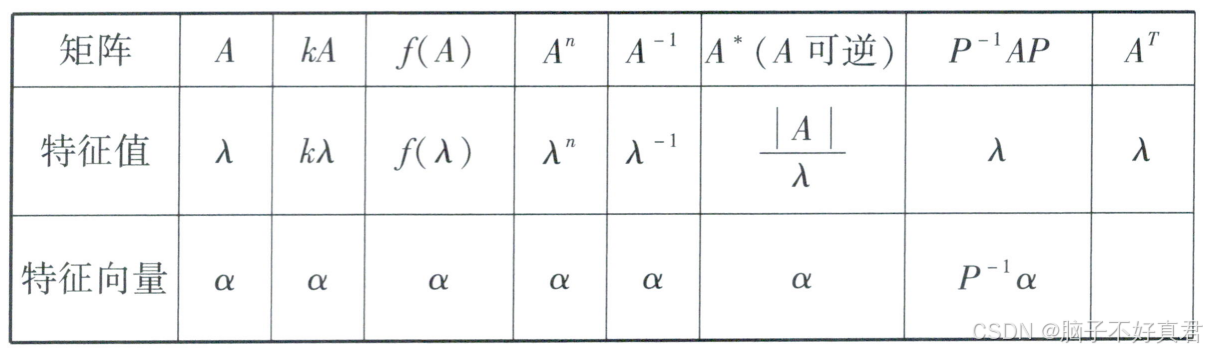
(3) 

(4)

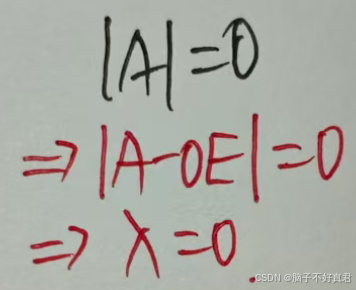
(5)

(6)

(7)同一特征值所对应的特征向量的线性组合仍然是该矩阵的特征向量.

(8)

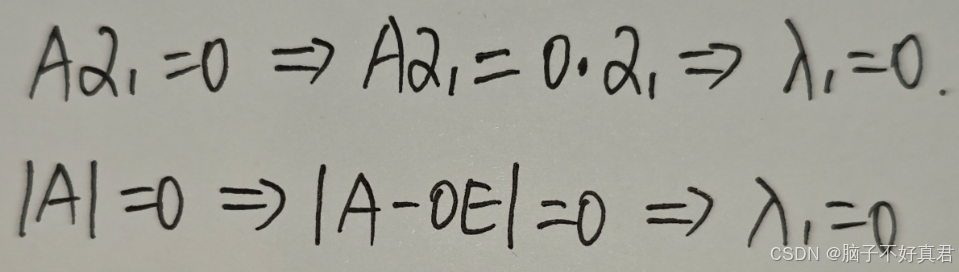
(9)基础解系中向量个数 = n - r(A)

(10)可对角化矩阵的秩=其非零特征值的个数.

(11)设三阶矩阵A的三个特征值：λ₁=-1，λ₂=0，λ₃=1，则方程组 AX = 0 的基础解系含有一个线性无关的解向量.

特征值全为单根⟹矩阵A可对角化.

可对角化矩阵的秩=其非零特征值的个数⟹r(A)= 2.

基础解系中向量个数= n-r(A).

基础解系中线性无关的解向量个数 = n- r(A) = 3-2 = 1.

(12)不同特征值对应的特征向量线性无关. 

(13)实对称矩阵一定可以相似对角化；实对称矩阵一定可以正交对角化.

(14)两个实对称矩阵合同⇔它们有相同的正惯性指数和负惯性指数（即它们有相同数量的正特征值和负特征值）。

(15)实对称的特征值都是实数. 

(16)对于任何一个方阵的任何一个特征值，都必然满足：代数重数≥几何重数(对应的线性无关的特征向量的个数)≥1，即 每个特征值的代数重数≥它的几何重数(这个特征值对应的线性无关的特征向量的个数)≥1.

(17)λ₀ 对应的特征向量是 (λ₀E - A)X = 0 的所有非零解.

(18)任何一个特征值都对应无数个特征向量.

(19) 两个齐次线性方程组 Ax = 0 和 Bx = 0 同解的充要条件是：它们的系数矩阵 A 和 B 行等价.
行等价：如果矩阵 B 可以通过对矩阵 A 进行有限次初等行变换得到，那么 A 和 B 就是行等价的，即存在可逆矩阵P使得 PA=B.

(20)两个矩阵等价⇔它们的秩相同、存在可逆矩阵P、Q使得 B=PAQ.

(21)
 

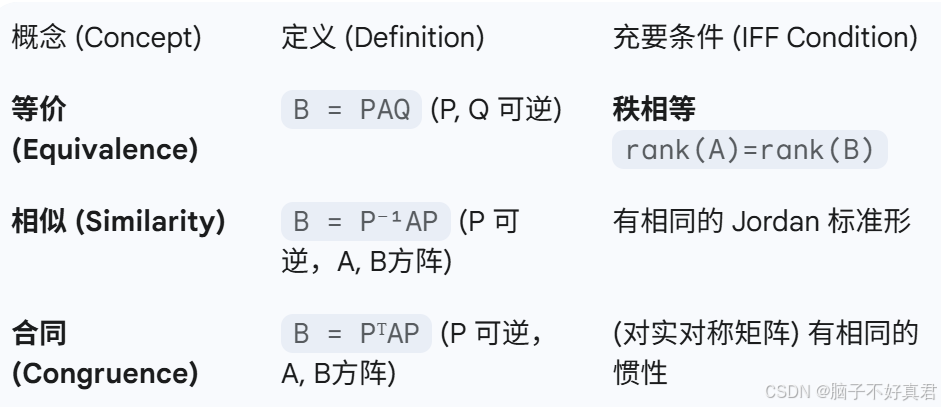
(22)可对角化矩阵的对角矩阵元素是原矩阵的特征值.

(23)方阵的特征值个数=其列数（计入重根） .