CCF-GESP 等级考试 2025年6月认证C++六级真题解析
1 单选题(每题 2 分,共 30 分)
第 1 题 下列哪一项不是面向对象编程的基本特征?
A. 继承 B. 封装 C. 多态 D. 链接
解析:答案D。面向对象编程的基本特征包含封装、继承、多态和抽象四大核心要素,这四大特征共同构成了代码组织的核心范式,有效提升了程序的可维护性、扩展性和复用性。所以D.不是。故选D。
第2题 为了让 Dog 类的构造函数能正确地调用其父类 Animal 的构造方法,横线线处应填入( )。
- class Animal {
- public:
- std::string name;
- Animal(std::string str) : name(str) {
- std::cout << "Animal created\n";
- }
- virtual void speak() {
- cout << "Animal speaks" << endl;
- }
- };
- class Dog : public Animal {
- std::string breed;
- public:
- Dog(std::string name, std::string b) : _________________, breed(b) {
- std::cout << "Dog created\n";
- }
- void speak() override {
- cout << "Dog barks" << endl;
- }
- };
- int main() {
- Animal* p = new Dog("Rex", "Labrador");
- p->speak();
- delete p;
- return 0;
- }
A. Animal(name) B. super(name) C. Animal::Animal(name) D. Animal()
解析:答案A。第25行。所以A.正确。super是Java或Python等语言的语法,C++不支持 super 关键字,所以B.错误。虽然语法上可以编译,但C++构造函数初始化列表的标准写法是直接使用类名 Animal(name),而不是 Animal::Animal(name),所以C.错误。父类 Animal 没有默认构造函数(它只有带 std::string 参数的构造函数),因此不能无参调用,所以D.错误。故选A。
第3题 代码同上一题,代码执行结果是( )。
A. 输出 Animal speaks B. 输出 Dog barks C. 编译错误 D. 程序崩溃
解析:答案B。对象构造阶段:当执行 new Dog("Rex", "Labrador") 时,会先调用父类 Animal 的构造函数,输出 Animal created。接着调用 Dog 的构造函数,输出 Dog created。多态调用阶段:p->speak() 通过父类指针调用虚函数,由于 Dog 类重写了 speak() 方法,实际执行的是 Dog::speak(),输出 Dog barks。故选B。
第4题 以下关于栈和队列的代码,执行后输出是( )。
- stack s;
- queue q;
- for (int i = 1; i <= 3; ++i) {
- s.push(i);
- q.push(i);
- }
- cout << s.top() << " " << q.front() << endl;
A. 1 3 B. 3 1 C. 3 3 D. 1 1
解析:答案B。栈是先进后出,队列是先进先出。栈压入顺序为1、2、3,栈顶为3,s.top()输出为3;队列压入顺序为1、2、3,队列的队头(队首)为1,q.front()输出为1。故选B。
第5题 在一个循环队列中,front是指向队头的指针,rear指向队尾的指针,队列最大容量为maxSize。判断 队列已满的条件是( )。
A. rear == front B. (rear + 1) % maxSize == front
C. (rear - 1 + maxSize) % maxSize == front D. (rear - 1) == front
解析:答案B。队满条件是循环队列满时,队尾指针 rear 的下一个位置(即 (rear + 1) % maxSize)会指向队头指针 front。A (rear == front):这是队列为空的判断条件。C ((rear - 1 + maxSize) % maxSize == front):逻辑等价于 (rear - 1) % maxSize == front,与D.相同,不符合循环队列满的定义。D ((rear - 1) == front):未考虑循环特性,且与标准定义不符。故选B。
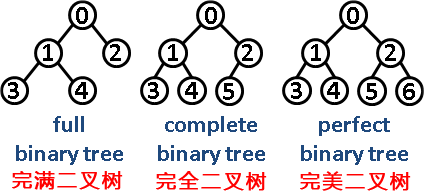
第6题 ( )只有最底层的节点未被填满,且最底层节点尽量靠左填充。
A. 完美二叉树 B. 完全二叉树 C. 完满二叉树 D. 平衡二叉树
解析:答案B。完美二叉树(Perfect Binary Tree):一个深度为k(>=1)且有2^(k-1) - 1个结点的二叉树称为完美二叉树。(注:国内的数据结构教材大多翻译为"满二叉树")。完全二叉树(Complete Binary Tree):完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。完满二叉树(Full Binary Tree):所有非叶子结点的度都是2。(只要你有孩子,你就必然是有两个孩子。)所以B.正确。故选B。
第7题 在使用数组表示完全二叉树时,如果一个节点的索引为i(从0开始计数),那么其左子节点的索引通常是( )。
A.(i-1)/2 B.i+1 C.i+2 D.2*i+1
解析:答案D。在使用数组表示完全二叉树时,节点的索引从0开始,其子节点的索引计算规则为:左子节点的索引为2*i + 1,右子节点的索引为2*i + 2。例如:根节点 i = 2:左子节点 i = 2*2 + 1 = 5,右子节点 i = 2*2 + 2 = 6,D.正确。故选D。
第8题 已知一棵二叉树的前序遍历序列为 GDAFEMHZ ,中序遍历序列为 ADFGEHMZ ,则其后序遍历序列为( )。
A. ADFGEHMZ B. ADFGHMEZ C. AFDGEMZH D. AFDHZMEG
解析:答案D。由前序遍历序列可知根节点为G,由中序遍历序列可知左树为AFD,右树为EHMZ,后序遍历序列左树、右树、根节点,只有D.的结构符合。具体:前序遍历(根-左-右)的第一个元素 G 是根节点。中序遍历(左-根-右)中,G 左侧 ADF 是左子树,右侧 EMHZ 是右子树。前序遍历左子树 DAF ,中序遍历左树 ADF,D子树根,左节点A,右节点F。前序遍历右子树EMHZ,中序遍历右子树EHMZ,E为子树根,只有右子树。前序遍历E右子树MHZ,中序遍历E右子树HMZ,M为子树根,左节点为H,右节点为Z。构成二叉树为:
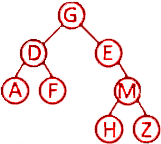
所以后序遍历序列为AFDHZMEG,D.正确。故选D。
第9题 设有字符集 {a, b, c, d, e},其出现频率分别为 {5, 8, 12, 15, 20},得到的哈夫曼编码为( )。
A. |
| B. |
| C. |
| D. |
|
解析:答案A。哈夫曼编码的特点,频率低的用长编码,频率高的用短编码。a最低,b次之,d次高,e最高,e短编码、a长编码,d短编码,b长编码,只有A.符合。具体:
a合并b为13,c合并13(ab)为25,d合并e为35,25合并35为60。
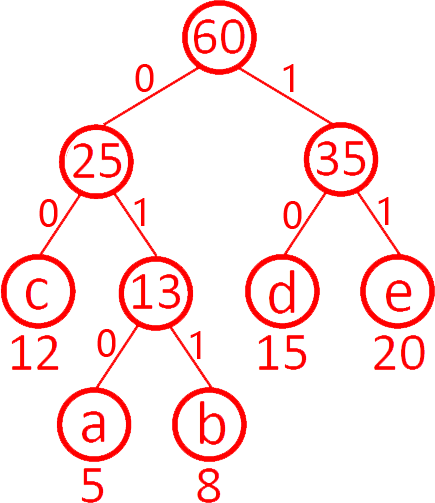
A.正确。故选A。
第10题 3位格雷编码中,编码 101 之后的下一个编码不可能是( )。
A. 100 B. 111 C. 110 D. 001
解析:答案C。格力雷编码中,相邻两处码只有一位变化。A.、B.、D.只发生一位变化,C. 除第2位由0变1个,第3位变由1变0,发生两位变化,所以C.不可能。故选C。
第11题 请将下列 C++ 实现的深度优先搜索(DFS)代码补充完整,横线处应填入( )。
- struct TreeNode {
- int val;
- TreeNode* left;
- TreeNode* right;
- TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
- };
- void dfs(TreeNode* root, vector& result) {
- if (root == nullptr) return;
- __________________________
- }
A. |
| B. |
|
C. |
| D. |
|
解析:答案A。题目要求补充一个深度优先搜索(DFS)的代码片段,二叉树的深度优先分为:先序遍历、中序遍历、后序遍历。观察选项可以发现,result.push_back()都在第1行,属前序遍历,属前序遍历顺序是:根节点 → 左子树 → 右子树,因此应 push_back(root->val),再递归遍历左、右子树。其他选项(如 push_back(root->left->val)或 push_back(root->right->val))会导致遍历顺序错误。具体:A.(根-左-右)符合前序遍历逻辑,所以正确。B.(先左子节点,再右子树,最后左子树)顺序错误,所以错误。C.(先左子节点,再左子树,最后右子树),顺序错误,所以错误。D.(先右子节点,再右子树,最后左子树)顺序错误,所以错误。故选A。
.第12题 给定一个二叉树,返回每一层中最大的节点值,结果以数组形式返回,横线处应填入( )。
- #include<vector>
- #include<queue>
- #include<algorithm>
- struct TreeNode {
- int val;
- TreeNode* left;
- TreeNode* right;
- TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
- };
- vector largestValues(TreeNode* root) {
- vector<int> result;
- if (!root) return result;
- queue<TreeNode*> q;
- q.push(root);
- while (!q.empty()) {
- int sz = q.size();
- int maxVal = INT_MIN;
- for (int i = 0; i < sz; ++i) {
- TreeNode* node;
- _______________________________
- maxVal = max(maxVal, node->val);
- if (node->left) q.push(node->left);
- if (node->right) q.push(node->right);
- }
- result.push_back(maxVal);
- }
- return result;
- }
A. |
| B. |
| C. |
| D. |
|
解析:答案D。在BFS层序遍历中,正确的队列操作顺序应为:先获取队首节点,再将该节点出队。node = q.front(); 获取当前待处理节点,q.pop(); 将该节点移出队列,所以D.正确。A.错误使用q.end()获取迭代器而非节点。B.缺少出队操作会导致死循环。C.先出队会导致获取错误节点。故选D。
第13题 下面代码实现一个二叉排序树的插入函数(没有相同的数值),横线处应填入( )。
- struct TreeNode {
- int val;
- TreeNode* left;
- TreeNode* right;
- TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
- };
- void insert(TreeNode*& root, int key) {
- if (!root) {
- root = new TreeNode(key);
- return;
- }
- _______________________________
- }
A. |
| B. |
|
C. |
| D. |
|
解析:答案A。题目要求实现二叉排序树(BST)的插入操作,且不允许重复值。BST的插入规则是:(1)如果当前节点为null,创建新节点。(2)如果 key 小于当前节点值,递归插入左子树。(3)如果 key 大于当前节点值,递归插入右子树。因不允许重复值,所以相等示处理。A.正确实现BST插入逻辑(左小右大),所以正确。B.左大右小,逻辑反了,所以错误。C.同时插入左右子树,破坏BST性质,所以错误。D:同时插入左右子树,且先右后左,完全错误。故选A。
第14题 以下关于动态规划算法特性的描述,正确的是( )。
A. 子问题相互独立,不重叠 B. 问题包含重叠子问题和最优子结构
C. 只能从底至顶迭代求解 D. 必须使用递归实现,不能使用迭代
解析:答案B。关于动态规划算法特性的描述,以下结论是正确的:动态规划的核心特征之一是存在重叠子问题(即子问题被重复计算多次)和最优子结构(问题的最优解包含其子问题的最优解)。子问题相互独立,不重叠:这是分治法的特征,动态规划的子问题通常不独立且存在重叠,所以A.错误。动态规划的核心特征之一是存在重叠子问题(即子问题被重复计算多次)和最优子结构(问题的最优解包含其子问题的最优解),所以B.正确。动态规划可以采用自底向上(迭代)或自顶向下(递归+记忆化)方式实现,所以C.错误。动态规划可通过迭代高效实现,递归仅为可选方式,所以D.错误。原谅选B。
第15 题 给定n个物品和一个最大承重为W的背包,每个物品有一个重量wt[i]和价值val[i],每个物品只能选择放或不放。目标是选择若干个物品放入背包,使得总价值最大,且总重量不超过W。关于下面代码,说法正确的是( )。
- int knapsack1D(int W, vector& wt, vector& val, int n) {
- vector dp(W+1, 0);
- for (int i = 0; i < n; ++i) {
- for (int w = W; w >= wt[i]; --w) {
- dp[w] = max(dp[w], dp[w - wt[i]] + val[i]);
- }
- }
- return dp[W];
- }
A. 该算法不能处理背包容量为 0 的情况
B. 外层循环 i 遍历背包容量,内层遍历物品
C. 从大到小遍历 w 是为了避免重复使用同一物品
D. 这段代码计算的是最小重量而非最大价值
解析:答案C。这是一个 0/1背包问题的动态规划解法,目标是选择部分物品放入背包,使得总价值最大且总重量不超过 W。代码初始化 dp[0] = 0,表示空背包价值为0,能够正确处理 W = 0 的情况,所以A.错误。程序实际是外层循环遍历物品(i),内层循环遍历背包容量(w),所以B.错误。w 从 W 递减到 wt[i],确保每个物品仅被计算一次(0/1背包特性),所以C.正确。代码通过 max(dp[w], dp[w - wt[i]] + val[i]) 计算的是最大价值,所以D.错误。故选C。
2 判断题(每题 2 分,共 20 分)
第1题 构造函数可以被声明为 virtual。( )
解析:答案错误。在C++中,并非所有类函数都可以声明为虚函数。允许声明为虚函数的条件:必须是类的非静态成员函数,且通过virtual关键字声明。禁止声明为虚函数的情况:构造函数:虚函数表(vtable)在构造函数执行时尚未初始化,逻辑矛盾;静态成员函数:静态函数不依赖对象实例,无法实现运行时多态;内联函数:编译时展开,与虚函数的动态绑定机制冲突;友元函数:C++不支持友元函数继承,无法通过虚机制调用;普通函数(非成员函数):多态性依托于类层次结构,普通函数不具备此特性。析构函数:通常应声明为虚函数,以确保通过基类指针删除对象时正确调用派生类析构函数避免资源泄漏(如动态内存未释放)。故错误。
第2题 给定一组字符及其出现的频率,构造出的哈夫曼树是唯一的。( )
解析:答案错误。当存在多个相同权值的节点时,合并顺序不同会导致不同的树形结构。例如,频率集合{2,2,3,3},因同频次序调整,可能生成多种不同形态的哈夫曼树,但他们的带权路径长度(WPL)是相同的。故错误。
第3题 为了实现一个队列,使其出队操作(pop)的时间复杂度为O(1)并且避免数组删除首元素的O(n)问题,一种常见且有效的方法是使用环形数组,通过调整队首和队尾指针来实现。( )
解析:答案正确。题目描述的实现队列的方式是环形数组(循环队列),其核心思路确实是通过调整队首(front)和队尾(rear)指针来高效进行出入队操作,避免移动数组元素的开销。环形数组的:当队尾指针到达数组末尾时,可以绕回到数组开头(环形结构),避免频繁扩容或移动元素。入队(push):rear = (rear + 1) % capacity(O(1));出队(pop):front = (front + 1) % capacity(O(1))。传统数组队列删除首元素需要移动后续所有元素(O(n)),而环形队列仅需移动指针(O(1))。故正确。
第4题 对一棵二叉排序树进行中序遍历,可以得到一个递增的有序序列。( )
解析:答案正确。二叉排序树的定义:
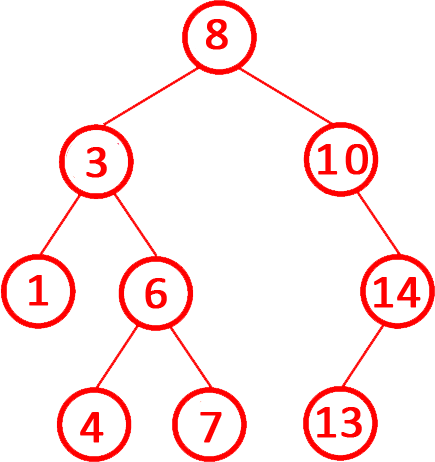
左子树的所有节点值 小于 当前节点值。右子树的所有节点值 大于 当前节点值。
中序遍历(左-根-右)的特性:先遍历左子树(所有值更小),再访问根节点,最后遍历右子树(所有值更大)。因此,中序遍历结果必然按升序排列。故正确。
第5题 如果二叉搜索树在连续的插入和删除操作后,所有节点都偏向一侧,导致其退化为类似于链表的结构,这时其查找、插入、删除操作的时间复杂度会从理想情况下的O(log n)退化到O(n log n)。( )
解析:答案错误。二叉搜索树(BST)又称二叉查找树或二叉排序树。题目考察二叉搜索树(BST)退化后的时间复杂度,判断其查找、插入、删除操作是否会从 O(log n) 退化为 O(n log n)。理想情况(平衡BST)查找、插入、删除的时间复杂度为O(log n)。退化情况(退化为链表):树高度变为n,操作需遍历所有节点,时间复杂度退化为 O(n)。
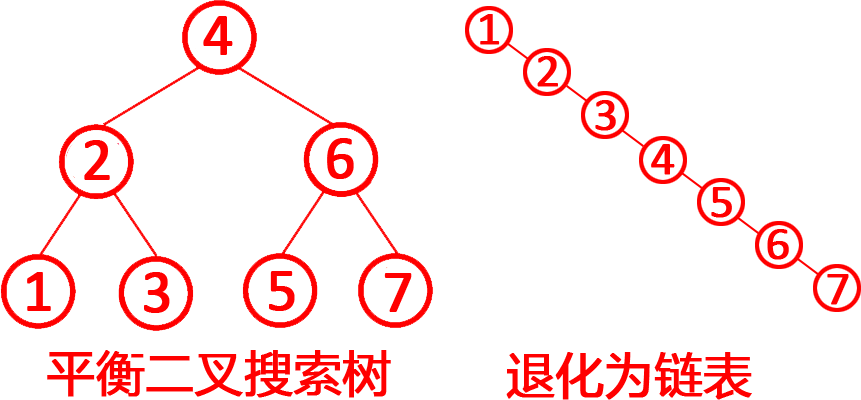
退化原因:若插入或删除的序列有序(如连续递增或递减),BST会退化为单侧链表,树高度从 log n 变为 n。如上图所示。查找:需遍历整条“链”,时间复杂度 O(n)。插入/删除:同样需遍历到末端或目标位置,时间复杂度O(n),而不是O(n log n),所以错误。
第6题 执行下列代码,my_dog.name的最终值是Charlie。( )
- class Dog {
- public:
- std::string name;
- Dog(std::string str) : name(str) {}
- };
- int main() {
- Dog my_dog("Buddy");
- my_dog.name = "Charlie";
- return 0;
- }
解析:答案正确。构造函数初始化(第4行):Dog(std::string str) : name(str) {}name为传入的字符串。第8行用Dog类建my_dog对象my_dog("Buddy") 会调用构造函数,将 name 初始化为 "Buddy"。第9行给对象成员赋值,修改成员变量,my_dog.name = "Charlie"; 显式修改name的值为"Charlie",my_dog.name 的最终值为 "Charlie",所以正确。
第7题 下列 C++ 代码可以成功编译,并且子类 Child 的实例能通过其成员函数访问父类 Parent 的属性 value 。( )
- class Parent {
- private:
- int value = 100;
- };
- class Child : public Parent {
- public:
- int get_private_val() {
- return value; // 尝试访问父类的私有成员
- }
- };
解析:答案错误。Parent::value 被声明为 private,根据C++访问控制规则,私有成员仅允许在声明它们的类内部访问,子类无法直接访问;即使子类 Child 使用 public 继承 Parent,父类的私有成员仍对子类不可见。尝试在 Child::get_private_val() 中直接访问 value 会导致编译错误。由于原代码中 Child 直接访问 Parent 的私有成员 value 违反C++访问控制规则,所以无法通过编译。故错误。
第8题 下列代码中的 tree 向量,表示的是一棵完全二叉树( -1 代表空节点)按照层序遍历的结果。( )
- #include< vector>
- std::vector tree = {1, 2, 3, 4, -1, 6, 7};
解析:答案错误。完全二叉树的定义:除最后一层外,其他层节点必须完全填充(无空缺)。最后一层节点从左到右连续排列(不能有中间空缺)。层序遍历结果:[1, 2, 3, 4, -1, 6, 7](-1 表示空节点)。
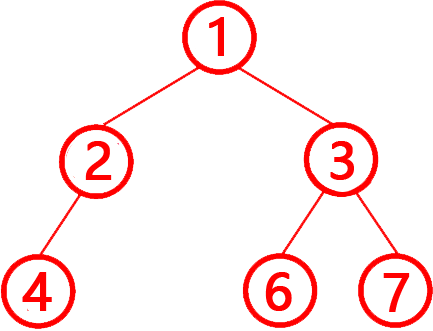
第3层(节点索引4):值为 -1(空节点,参考上图),但后续仍有 6 和 7 节点。违反完全二叉树“最后一层节点从左到右连续排列(不能有中间空缺)”的规则,该树不是完全二叉树,所以错误。
第9题 在树的深度优先搜索(DFS)中,使用栈作为辅助数据结构以实现“先进后出”的访问顺序。( )
解析:答案正确。树的深度优先搜索(DFS)确实使用栈作为辅助数据结构,其“先进后出”(FILO)特性确保优先深入探索分支,符合DFS的核心逻辑。故正确。
第10题 下面代码采用动态规划求解零钱兑换问题:给定 𝑛 种硬币,第 𝑖 种硬币的面值为 𝑐𝑜𝑖𝑛𝑠[𝑖 − 1] ,目标金额为 𝑎𝑚𝑡 ,每种硬币可以重复选取,求能够凑出目标金额的最少硬币数量;如果不能凑出目标金额,返回 -1 。( )
- int coinChangeDPComp(vector &coins, int amt) {
- int n = coins.size();
- int MAX = amt + 1;
- vector dp(amt + 1, MAX);
- dp[0] = 0;
- for (int i = 1; i <= n; i++) {
- for (int a = 1; a <= amt; a++) {
- if (coins[i - 1] > a)
- dp[a] = dp[a];
- else
- dp[a] = min(dp[a], dp[a - coins[i - 1]] + 1);
- }
- }
- return dp[amt] != MAX ? dp[amt] : -1;
- }
解析:答案正确。动态规划状态定义:dp[a]表示凑出金额a所需的最少硬币数,初始化时设为MAX不可达状态)。dp[0] = 0是边界条件,表示金额为0时不需要硬币。状态转移方程:对于每种硬币coins[i-1],若其面值小于等于当前金额a,则更新dp[a]为min(dp[a], dp[a - coins[i-1]] + 1)。若硬币面值大于 a,则保持dp[a]不变(代码第10-13行)。遍历顺序:外层循环遍历硬币种类(i),内层循环遍历金额(a),确保每种硬币可重复使用(完全背包问题)。若 dp[amt] 未被更新(仍为 MAX),说明无法凑出目标金额,返回 -1;否则返回 dp[amt]。所以代码逻辑正确,符合动态规划解决零钱兑换问题的标准实现。故正确。
3 编程题(每题 25 分,共 50 分)
3.1 编程题1
- 试题名称:学习小组
- 时间限制:1.0 s
- 内存限制:512.0 MB
3.1.1 题目描述
班主任计划将班级里的𝑛名同学划分为若干个学习小组,每名同学都需要分入某一个学习小组中。观察发现,如果一个学习小组中恰好包含𝑘名同学,则该学习小组的讨论积极度为aₖ。
给定讨论积极度a₁, a₂,...,aₙ,请你计算将这𝑛名同学划分为学习小组的所有可能方案中,讨论积极度之和的最大值。
3.1.2 输入格式
第一行,一个正整数𝑛,表示班级人数。
第二行,𝑛个非负整数a₁, a₂,...,aₙ,表示不同人数学习小组的讨论积极度。
3.1.3 输出格式
输出共一行,一个整数,表示所有划分方案中,学习小组讨论积极度之和的最大值。
3.1.4 样例
3.1.4.1 输入样例1
- 4
- 1 5 6 3
3.1.4.2 输出样例1
- 10
3.1.4.3 输入样例2
- 8
- 0 2 5 6 4 3 3 4
3.1.4.4 输出样例2
- 12
3.1.5 数据范围
对于40%的测试点,保证1≤𝑛≤10。
对于所有测试点,保证1≤𝑛≤1000,0≤aᵢ≤10⁴。
3.1.6 编写程序思路
分析:题目是分组优化问题:给定 n 名同学和一组讨论讨论积极度a₁,a₂,...,aₙ(其中aₖ表示一个小组恰好有k名同学时的讨论积极度),目标是将所有同学划分为若干个学习小组(每个小组至少包含 1 名同学),使得所有小组的讨论讨论积极度之和最大。每个同学必须被分配到恰好一个小组中,小组大小k可以是1到n之间的任意整数,且小组大小k对应的讨论积极度aₖ由输入给出(非负整数)。目标函数:最大化所有小组的讨论积极度之和。该问题可以建模为一个完全背包问题:"物品" 对应于小组大小k(k=1,2,...,n),每种物品可以无限次使用(即可以创建多个相同大小的小组);"物品重量" 为小组大小k;"物品价值" 为讨论积极度aₖ。"背包容量" 为总人数n,要求恰好装满背包(所有同学都被分配)。可以使用动态规划(DP)求解,状态定义为:dp[i] 表示分配i 名同学时能获得的最大讨论积极度之和。初始状态:dp[0]=0(0名同学时讨论积极度为0)。状态转移:对于i名同学,枚举最后一个小组的大小k(1≤k≤i),则剩余i−k名同学的最优解为dp[i−k],因此:dp[i]= max{dp[i−k]+ak},其中1≤k≤i。最终答案为dp[n]。完整参考实现代码如下:
#include <iostream>
using namespace std;const int N = 1005;
int n, a[N], dp[N];int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];for (int k = 1; k <= i; k++)dp[i] = max(dp[i], dp[i - k] + a[k]);}cout << dp[n] << endl;return 0;
}3.2 编程题2
- 试题名称:最大因数
- 时间限制:1.0 s
- 内存限制:512.0 MB
3.2.1 题目描述
给定一棵有10⁹个结点的有根树,这些结点依次以1,2,...,10⁹编号,根结点的编号为1。对于编号为k(2≤k≤10⁹)的结点,其父结点的编号为k的因数中除k以外最大的因数。
现在有q组询问,第i(1≤k≤q)组询问给定xᵢ,yᵢ,请你求出编号分别为xᵢ,yᵢ的两个结点在这棵树上的距离。两个结点之间的距离是连接这两个结点的简单路径所包含的边数。
3.2.2 输入格式
第一行,一个正整数q,表示询问组数。
接下来q行,每行两个正整数xᵢ,yᵢ,表示询问结点的编号。
3.2.3 输出格式
输出共q行,每行一个整数,表示结点xᵢ,yᵢ之间的距离。
3.2.4 样例
3.2.4.1 输入样例1
- 3
- 1 3
- 2 5
- 4 8
3.2.4.2 输出样例1
- 1
- 2
- 1
3.2.4.3 输入样例2
- 1
- 120 650
3.2.4.4 输出样例2
- 9
3.2.5 数据范围
对于60% 的测试点,保证1≤xᵢ,yᵢ≤1000。
对于所有测试点,保证1≤q≤1000,1≤xᵢ,yᵢ≤10⁹。
3.2.6 编写程序思路
分析:题目给出了一棵特殊的树,其节点编号从1到10⁹,根节点为1。对于编号为k(k ≥ 2)的节点,其父节点是k的除k以外最大的因数。例如:节点2的父节点是1(2的因数有1和2,除2外最大是1);节点3的父节点是1(3的因数有1和3);节点4的父节点是2(4的因数有1、2、4,除4外最大是2);节点6的父节点是3(6的因数有1、2、3、6,除6外最大是3)。特点是质数全连在根结点上,质数与根1的距离为1,质数间距离为2。路径长度:如果两个节点x和y在树上的距离是d,那么它们的最近公共祖先(LCA)会出现在路径中。因此,我们可以先找到x和y的LCA,然后计算从x到LCA的距离和从y到LCA的距离,最后相加。如预先计算LCA,则时间复杂度为O(n log n),对后40%数据会超时。
解决方案:由于树高不超过O(log n),对n=10⁹树高不超过30。对于每个查询(x, y),先分别求x、y的节点序列直到根节点,再从分别从x、y开始边计算距离边找它们的LCA,两距离和即为结果。如120:节点序列为120,60,30,15,5,1(最小因素2,2,2,3,5),650:节点序列为650,325,65,13,1(最小因素2,5,5,13),LCA为1,120到1的边数为5,650到1的边数为4,故距离为9。
找因素的时间复杂度为O(n¹ᐟ²),找LCA求距离的时间复杂度O(log n)。总时间复杂度为O(q*n¹ᐟ²*log n))。对60%的数据n≤1000,O(q*n¹ᐟ²*log n))<600*31.63* 9.966=<189135,可忽略;对40%的数据n≤10⁹时O(q*n¹ᐟ²*log n)) <400*32000*30=384000000,10⁸级,基本不会超时。完整参考代码如下:
#include <iostream>
using namespace std;const int N = 35; //log₂10⁹≈29.8974<30<35int q;
int a[N], cntx; //a[N]存放a(xᵢ)的父节点序列,cntx为xᵢ到最近公共祖先距离
int b[N], cnty; //b[N]存放b(yᵢ)的父节点序列,cnty为yᵢ到最近公共祖先距离
int f[N], t; //f[N]某节点各节点的最小因素,t为节点深度void factor(int x, int a[], int &cnt) {a[0] = x; //x为某节点t = 0;for (int i = 2; i * i <= x; i++) //整数唯一分解定理,因子为不下降序列while (x % i == 0) { //求最小因数i。f[++t] = i; //记录最小因素(2<=i<=x¹ᐟ²)x /= i; //x除以i为最大因素,即父节点,继续求同因数(如果存在)}if (x > 1) //最后一个质因素f[++t] = x;for (int i = 1; i <= t; i++) //求x的所有节点a[i] = a[i - 1] / f[i]; //前一节点除以其最小因数即为最大因数(父节点)cnt = t; //节点深度
}int main() {cin >> q;while (q--) {int x, y;cin >> x >> y;factor(x, a, cntx); //返回a[0]为x节点,其他为其上的父节点直到根节点1factor(y, b, cnty); //返回b[0]为y节点,其他为其上的父节点直到根节点1int px = 0, py = 0;while (a[px] != b[py]) { //求x、y到最近公共祖先(a[px]==b[py])距离px、pyif (a[px] > b[py])px++;elsepy++;}cout << px+py << endl;}return 0;
}