牛客周赛 Round 101题解
题解的token计算
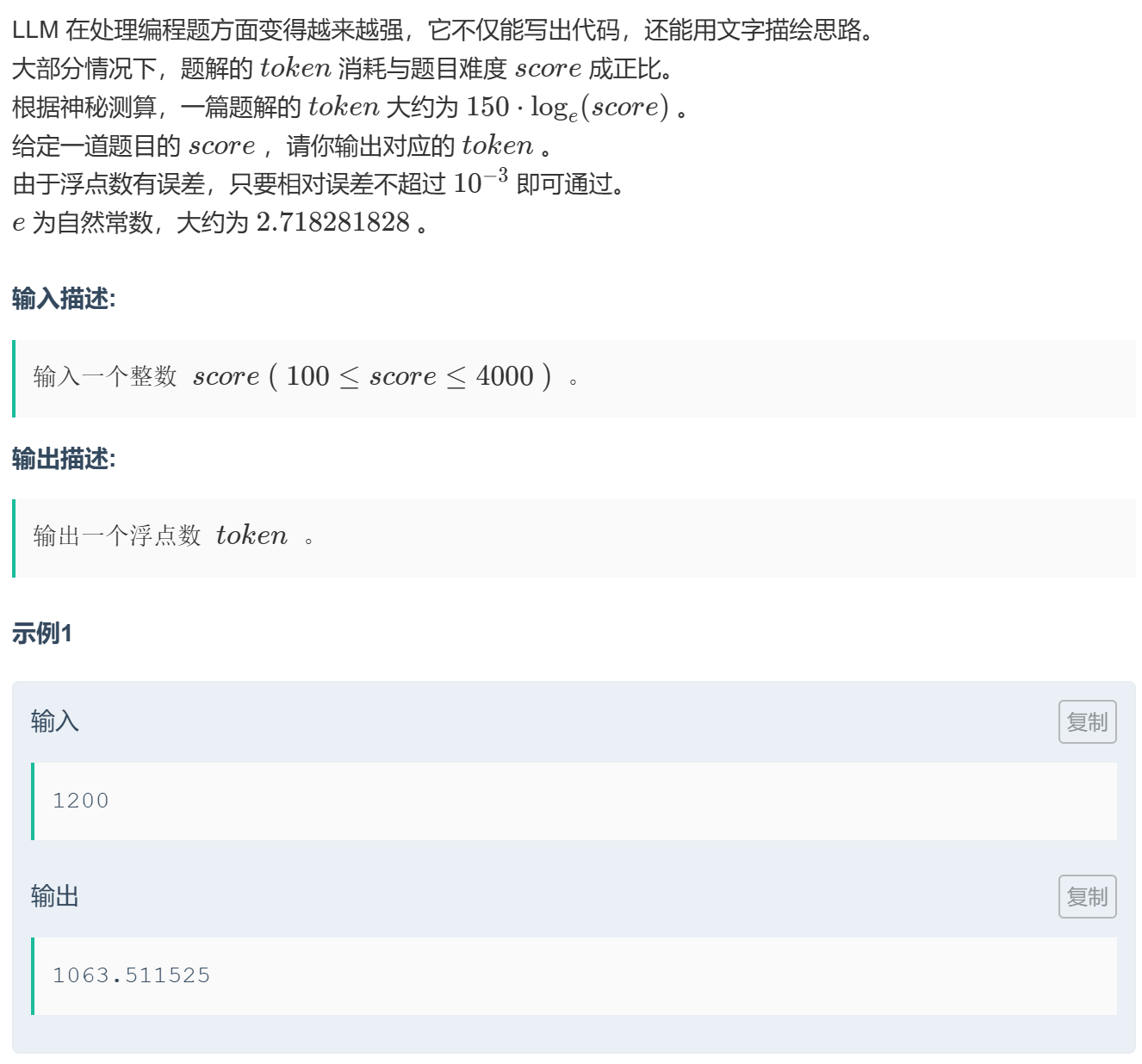
思路:直接按照题目上说的去计算一下即可
#include <bits/stdc++.h>
using namespace std;int main() {int n;cin >> n;cout << fixed << setprecision(6) << (double)(150 * log(n)) << endl;return 0;
}76修地铁

思路:按照提议去模拟即可,
对于普通火把,从第五个开始就开始每五列+2个
对于红石火把,就是从第五个开始,每十列+1个
对于普通铁轨,从第20列开始,每20列+3个
对于动力铁轨,除去动力铁轨,剩下的都是两个普通铁轨
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
signed main()
{cin >> n;int a = (n >= 5) ? ((n - 5) / 5 + 1) * 2 : 0;int b = (n >= 5) ? ((n - 5) / 10 + 1) : 0;int c = (n >= 20) ? ((n - 20) / 20 + 1) * 3 : 0;int flag = (n >= 20) ? ((n - 20) / 20 + 1) : 0;int d = (n - flag) * 2;cout << a << " " << b << " " << c << " " << d;return 0;
}76选数
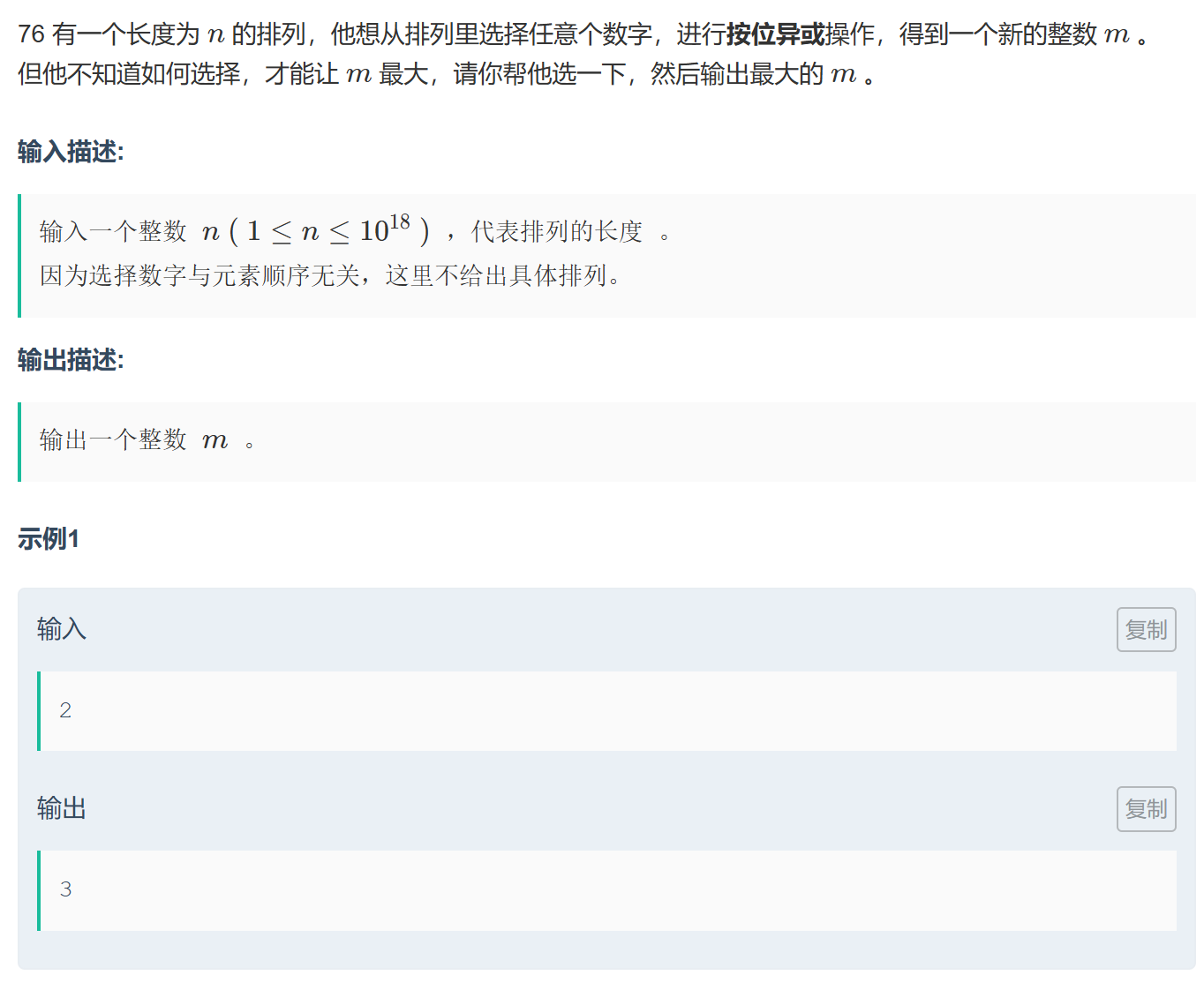
思路:很明显我们会发现就是排列里面的在二进制位里面的所有数的累加和,比如说当前n=5,那么就是1+2+4,所以我们只需要去遍历那个位置的1<<bit>n,然后输出这个(1<<bit)-1即可
#include<bits/stdc++.h>
using namespace std;
#define int long longsigned main() {int n;cin >> n;int pos = 0;while ((1LL << (pos + 1)) <= n) {pos++;}cout << (1LL << (pos + 1)) - 1;return 0;
}76构造

思路:我们很容易发现分割的区间里面必然会存在gcd(l,r)=1的情况,因为排列里面始终有一个1,所以,如果m为偶数就是直接输出-1,然后我们再来考虑,如果m是奇数,那么就将m的二进制位里面除了1大小的那一位,别的都单独作为一段,最后的1和剩下的数作为一段,然后输出段数和区间即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
vector<int> alone;
map<int,int> mp;
signed main()
{cin>>n>>m;if(m%2==0){cout<<"-1\n";return 0;}for(int i=31;i>=0;i--){if(m&(1<<i)){if((1<<i)>n){cout<<"-1\n";return 0;}if(i==0&&m%2==1){break;}alone.push_back(1<<i);}}int l=1;vector<pair<int,int> > pos;for(int i:alone){cout<<i<<" ";mp[i]++;pos.push_back({l,l});l++;}for(int i=1;i<=n;i++){if(mp[i]==0){cout<<i<<" ";}}cout<<"\n";pos.push_back({l,n});cout<<pos.size()<<"\n";for(auto v:pos){cout<<v.first<<" "<<v.second<<"\n";}return 0;
}qcjj寄快递

思路:我们这题其实在题面上已经告诉你时间是多少了,就是形式化题面那个式子,我们只需要对式子去进行求导,找到零点就是最后的答案,此时的k= log2(e+ln(2)),我们只需要对每一步的欧式距离去求导,然后带入原式子求出最小的时间去累加即可
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define double long double
struct node
{double x, y;
};
double cal(const node &a, const node &b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}
double com(double e)
{if (e == 0.0){return 0.0;}double k = log2(e * log(2));if (k < 0.0){k = 0.0;}return 2 * k + 2 * e / pow(2,k);
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<node> points(n);for (int i = 0; i < n; ++i){cin >> points[i].x >> points[i].y;}double ans = 0.0;for (int i = 1; i < n; ++i){double e = cal(points[i - 1], points[i]);ans += com(e);}cout << fixed << setprecision(10) << ans << endl;return 0;
}幂中幂plus

思路:我们发现mod的大小不会超过1e6,因此是有循环节,我们只需要找到循环节的大小,和一个循环节的累加和就可以在O(1)的时间复杂度内求解所有的k
#include <bits/stdc++.h>
using namespace std;
using ll = long long;ll MOD;ll ksm(ll base, ll exp) {ll res = 1;base %= MOD;while (exp > 0) {if (exp % 2 == 1) {res = (res * base) % MOD;}base = (base * base) % MOD;exp /= 2;}return res;
}void solve() {ll b, c0;cin >> b >> c0 >> MOD;if (MOD == 1) {ll q;cin >> q;while (q--) {cout << 0 << "\n";}return;}vector<ll> memo(MOD + 1, -1);ll c = ksm(b, c0), cnt = 0;vector<ll> pre;pre.push_back(0);while (memo[c] == -1) {cnt++;memo[c] = cnt;pre.push_back((pre.back() + c) % MOD);c = ksm(b, c);}ll len = cnt - memo[c] + 1;ll su = (pre[cnt] - pre[memo[c] - 1] + MOD) % MOD;ll q;cin >> q;while (q--) {ll k;cin >> k;if (k <= cnt) {cout << pre[k] % MOD << "\n";} else {ll t = (k - memo[c] + 1) / len % MOD;ll ans = t * su % MOD;ans = (ans + pre[memo[c] - 1]) % MOD;ll r = (k - memo[c] + 1) % len;ans = (ans + pre[memo[c] - 1 + r] - pre[memo[c] - 1] + MOD) % MOD;cout << ans << "\n";}}
}int main() {ios_base::sync_with_stdio(false);cin.tie(nullptr);solve();return 0;
}