当前位置：首页 > news >正文

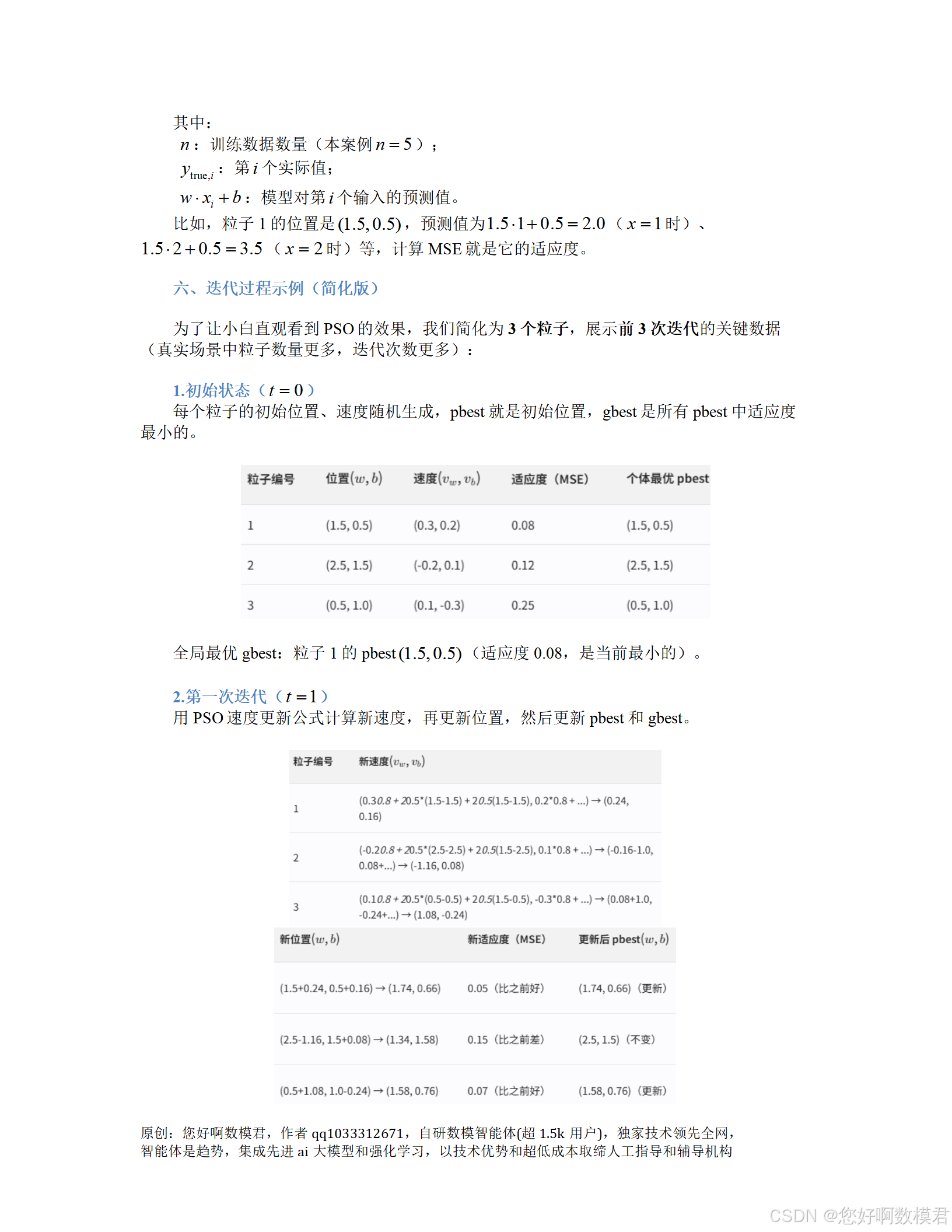
30天打牢数模基础-粒子群算法讲解

news 2025/7/21 8:20:05

import random
import numpy as np
import matplotlib.pyplot as plt# ------------------------------
# 1. 模拟训练数据（带噪声的线性数据）
# ------------------------------
# 真实模型：y = 2x + 1（w=2，b=1）
x_data = np.array([1, 2, 3, 4, 5])  # 输入x
y_true = 2 * x_data + 1 + np.random.uniform(-0.1, 0.1, size=x_data.shape)  # 带噪声的实际值
print("模拟训练数据：")
print(f"输入x: {x_data}")
print(f"实际值y_true: {y_true.round(2)}")# ------------------------------
# 2. 定义适应度函数（均方误差MSE，越小越好）
# ------------------------------
def calculate_mse(w, b, x, y):"""计算线性模型y=w*x + b的均方误差（MSE）参数：w: 权重（float）b: 偏置（float）x: 输入数据（numpy数组）y: 实际值（numpy数组）返回：mse: 均方误差（float）"""y_pred = w * x + b  # 模型预测值mse = np.mean((y - y_pred) ** 2)  # 均方误差计算公式return mse# ------------------------------
# 3. 初始化PSO参数（小白经典值）
# ------------------------------
n_particles = 30  # 粒子数量（平衡多样性与计算量）
w_inertia = 0.8  # 惯性权重（控制探索与细化的平衡）
c1 = 2  # 认知学习因子（重视自己的经验）
c2 = 2  # 社会学习因子（重视群体的经验）
max_iter = 100  # 最大迭代次数（足够收敛）# 位置范围（w和b的可行域）
w_min, w_max = 0, 4  # 权重w的范围（真实值为2）
b_min, b_max = 0, 2  # 偏置b的范围（真实值为1）# 速度范围（限制粒子移动速度，避免飞过头）
v_w_min, v_w_max = -1, 1  # w的速度范围
v_b_min, v_b_max = -0.5, 0.5  # b的速度范围# ------------------------------
# 4. 初始化粒子群（每个粒子代表一组(w,b)候选解）
# ------------------------------
particles = []
for _ in range(n_particles):# 随机初始化位置（w, b）：在可行域内随机取值w = random.uniform(w_min, w_max)b = random.uniform(b_min, b_max)# 随机初始化速度（v_w, v_b）：在速度范围内随机取值v_w = random.uniform(v_w_min, v_w_max)v_b = random.uniform(v_b_min, v_b_max)# 初始个体最优（pbest）：当前位置（因为还没有历史数据）pbest_w = wpbest_b = b# 计算初始pbest的适应度（MSE）pbest_fitness = calculate_mse(pbest_w, pbest_b, x_data, y_true)# 将粒子信息存入字典（方便管理）particles.append({'w': w,           # 当前w值'b': b,           # 当前b值'v_w': v_w,       # 当前w的速度'v_b': v_b,       # 当前b的速度'pbest_w': pbest_w,  # 个体最优w'pbest_b': pbest_b,  # 个体最优b'pbest_fitness': pbest_fitness  # 个体最优适应度（MSE）})# ------------------------------
# 5. 初始化全局最优（gbest：所有粒子pbest中的最优解）
# ------------------------------
gbest_w = particles[0]['pbest_w']  # 初始gbest的w（取第一个粒子的pbest）
gbest_b = particles[0]['pbest_b']  # 初始gbest的b（取第一个粒子的pbest）
gbest_fitness = particles[0]['pbest_fitness']  # 初始gbest的MSE
# 遍历所有粒子，找到真正的gbest（MSE最小）
for p in particles:if p['pbest_fitness'] < gbest_fitness:gbest_fitness = p['pbest_fitness']gbest_w = p['pbest_w']gbest_b = p['pbest_b']# ------------------------------
# 6. 迭代优化（核心过程）
# ------------------------------
fitness_history = []  # 记录每一代的gbest MSE（用于可视化）
for iter in range(max_iter):# 遍历每个粒子，更新速度、位置、pbestfor p in particles:# 生成随机数r1、r2（0到1之间，增加随机性）r1 = random.random()r2 = random.random()# ------------------------------# 更新速度（核心公式：惯性+认知+社会）# ------------------------------# w的速度更新：v_w = 惯性项 + 认知项（自己的经验） + 社会项（群体的经验）p['v_w'] = (w_inertia * p['v_w'] +c1 * r1 * (p['pbest_w'] - p['w']) +  # 认知项：向自己的pbest靠近c2 * r2 * (gbest_w - p['w']))         # 社会项：向群体的gbest靠近# b的速度更新（同理）p['v_b'] = (w_inertia * p['v_b'] +c1 * r1 * (p['pbest_b'] - p['b']) +c2 * r2 * (gbest_b - p['b']))# 限制速度在设定范围内（避免飞太快）p['v_w'] = max(min(p['v_w'], v_w_max), v_w_min)p['v_b'] = max(min(p['v_b'], v_b_max), v_b_min)# ------------------------------# 更新位置（位置 = 当前位置 + 速度）# ------------------------------p['w'] += p['v_w']  # 更新w的值p['b'] += p['v_b']  # 更新b的值# 限制位置在可行域内（避免飞出边界）p['w'] = max(min(p['w'], w_max), w_min)p['b'] = max(min(p['b'], b_max), b_min)# ------------------------------# 更新个体最优（pbest：保留自己的最佳经验）# ------------------------------current_fitness = calculate_mse(p['w'], p['b'], x_data, y_true)  # 当前位置的MSEif current_fitness < p['pbest_fitness']:  # 如果当前MSE更小，更新pbestp['pbest_w'] = p['w']p['pbest_b'] = p['b']p['pbest_fitness'] = current_fitness# ------------------------------# 更新全局最优（gbest：保留群体的最佳经验）# ------------------------------for p in particles:if p['pbest_fitness'] < gbest_fitness:  # 如果某个粒子的pbest更优，更新gbestgbest_fitness = p['pbest_fitness']gbest_w = p['pbest_w']gbest_b = p['pbest_b']# 记录当前代的gbest MSE（用于可视化）fitness_history.append(gbest_fitness)# 每10代打印一次进度（方便观察）if (iter + 1) % 10 == 0:print(f"迭代次数：{iter+1:2d}，当前gbest MSE：{gbest_fitness:.4f}")# ------------------------------
# 7. 输出优化结果
# ------------------------------
print("\n" + "-"*50)
print("PSO优化完成！")
print(f"最优权重w: {gbest_w:.4f}（真实值：2）")
print(f"最优偏置b: {gbest_b:.4f}（真实值：1）")
print(f"最小均方误差（MSE）: {gbest_fitness:.4f}")
print("-"*50 + "\n")# ------------------------------
# 8. 可视化结果（小白必看，直观理解优化过程）
# ------------------------------
# 图1：迭代次数与MSE变化（看是否收敛）
plt.figure(figsize=(10, 6))
plt.plot(range(max_iter), fitness_history, color='blue', linewidth=2, label='gbest MSE')
plt.xlabel('迭代次数', fontsize=12)
plt.ylabel('均方误差（MSE）', fontsize=12)
plt.title('PSO优化线性模型：迭代次数与MSE关系', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()# 图2：模型拟合效果（看是否接近真实数据）
plt.figure(figsize=(10, 6))
plt.scatter(x_data, y_true, color='red', s=100, label='实际数据（带噪声）')  # 实际数据点
x_plot = np.linspace(min(x_data)-1, max(x_data)+1, 100)  # 生成平滑的x轴数据
y_plot = gbest_w * x_plot + gbest_b  # 用最优参数计算预测值
plt.plot(x_plot, y_plot, color='blue', linewidth=2, label=f'拟合模型：y={gbest_w:.2f}x + {gbest_b:.2f}')
plt.xlabel('输入x', fontsize=12)
plt.ylabel('输出y', fontsize=12)
plt.title('PSO优化线性模型：拟合效果', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()