MLA：KV Cache 的“低秩跃迁”

MLA: Multi-head Latent Attention

• deepseek v2 论文

  https://arxiv.org/pdf/2405.04434

• [参考B站链接](【全网最细！DeepSeekMLA 多头隐变量注意力：从算法原理到代码实现】https://www.bilibili.com/video/BV1GnKLeTEyr?vd_source=7937b7ae341caaf55cd0ac02b03193a1)

  【全网最细！DeepSeekMLA 多头隐变量注意力：从算法原理到代码实现】https://www.bilibili.com/video/BV1GnKLeTEyr?vd_source=7937b7ae341caaf55cd0ac02b03193a1

• MHA、MQA、GQA：大模型注意力机制的演进

  https://blog.csdn.net/hbkybkzw/article/details/149311299

• KVCache是常用的技术，为了降低KVCache的存储量，GQA和MQA被提出来简化KV值，但是这些技术都会折损效果。

  MLA采用低秩压缩算法，压缩KV的维度，相比于MHA，MLA效果又好，推理效率又高。

---

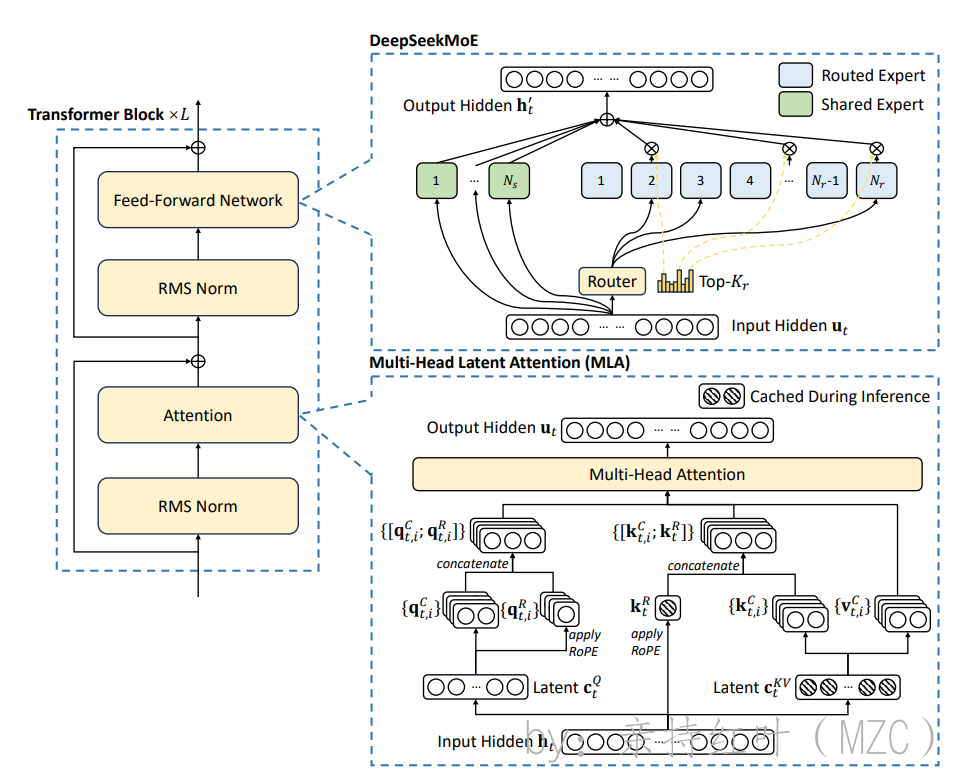
标准MHA算法

• 输入向量 (注意下面使用的q,k,v都是列向量维度)：

  $ q_t, k_t, v_t \in \mathbb{R}^{d_{n_h}} $：每个头的查询（query）、键（key）和值（value）向量，它们的维度为$d_{n_h} $

  1. $d$ 表示输入维度
  2. $n_h$ 表示头的数量
  3. $d_h$ 表示每个头的维度
  4. $h_t$ 表示输入的第t个向量

  $$\begin{array}{rl}{\mathbf{q}}_t& =W^Q{\mathbf{h}}_t,\\ {\mathbf{k}}_t& =W^K{\mathbf{h}}_t,\\ {\mathbf{v}}_t& =W^V{\mathbf{h}}_t,\end{array}$$

  $W^Q,W^K,W^V\in {\mathbb{R}}^{d_h{n}_h\times d}$ 表示输入维度，只用一个矩阵来处理多头

• 多头的输出拼接:

  每个头的输出结果都会被拼接（concatenate）
  $$\begin{gathered} [{\mathbf{q}}_{t,1};{\mathbf{q}}_{t,2};\dots ;{\mathbf{q}}_{t,n_h}]={\mathbf{q}}_t, \\ [{\mathbf{k}}_{t,1};{\mathbf{k}}_{t,2};\dots ;{\mathbf{k}}_{t,n_h}]={\mathbf{k}}_t, \\ [{\mathbf{v}}_{t,1};{\mathbf{v}}_{t,2};\dots ;{\mathbf{v}}_{t,n_h}]={\mathbf{v}}_t, \end{gathered}$$

• 注意力计算：

  对于每个头 ( i )，计算注意力输出 $${\mathbf{o}}_{t,i}$$：
  $${\mathbf{o}}_{t,i}=\sum _{j=1}^t{\text{Softmax}}_j\left(\frac{{\mathbf{q}}_{t,i}^T{\mathbf{k}}_{j,i}}{\sqrt{d_h}}+\mathrm{mask}\right){\mathbf{v}}_{j,i}$$
  其中：

  1. $${\mathbf{q}}_{t,i}^T{\mathbf{k}}_{j,i}$$是查询向量和键向量的点积。
  2. $$\sqrt{d_h}$$是缩放因子，用于稳定计算。
  3. $\mathrm{mask}$ 是掩码矩阵。
  4. $${\text{Softmax}}_j$$是沿着键的维度进行归一化的注意力权重。

• 最终输出：

  $q_t,k_t,v_t\in {\mathbb{R}}^{d_h{n}_h}$ 每个头输出结果进行concat
  $${\mathbf{u}}_t=W^O[{\mathbf{o}}_{t,1};{\mathbf{o}}_{t,2};\dots ;{\mathbf{o}}_{t,n_h}],$$

• kvcache占用
  $$2\cdot n_h\cdot d_h\cdot l$$
  其中 $l$ 为Decoder Layer层数

  ---

MLA算法

• MLA的核心是对KV做了低秩压缩，在送入标准MHA算法之前，用更短的一个向量来表示原来长的向量，从而大幅减少KV cache空间。

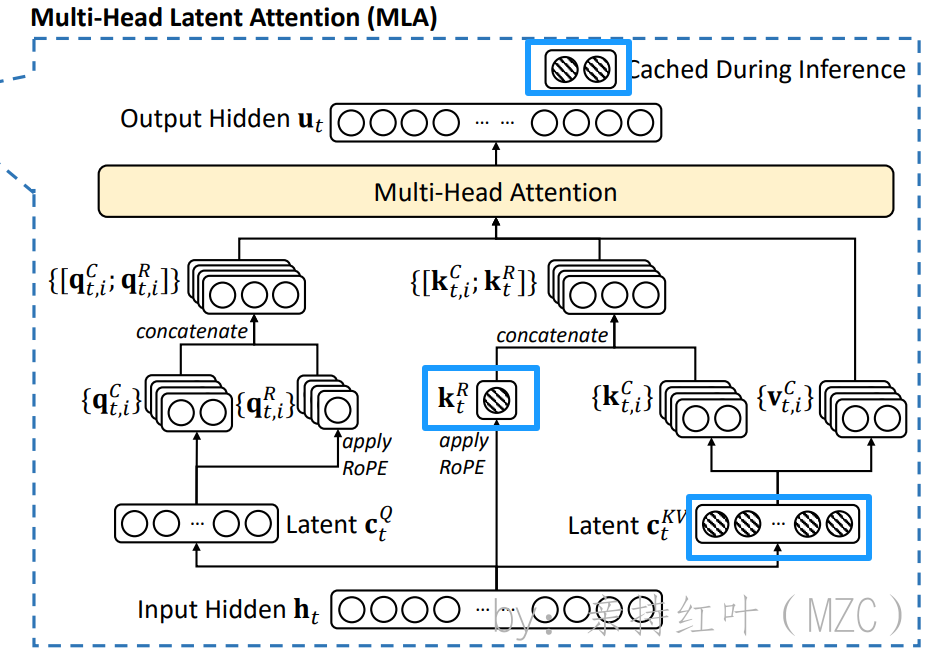
• 公式：
  $${\mathbf{c}}_t^{KV}=W^{DKV}{\mathbf{h}}_t,$$

  $${\mathbf{k}}_t^C=W^{UK}{\mathbf{c}}_t^{KV},$$

  $${\mathbf{v}}_t^C=W^{UV}{\mathbf{c}}_t^{KV}.$$

  1. 通过下采样矩阵，压缩得到中间表示，再通过上采样矩阵还原 KV：

     通过下采样矩阵 $ W^{DKV} $，将输入向量 $ \mathbf{h}_t $ 压缩为中间表示 $ \mathbf{c}_t^{KV} $。

     再通过上采样矩阵 $ W^{UK} $ 和 $ W^{UV} $，分别还原出压缩后的 $ \mathbf{k}_t^C $ 和 $ \mathbf{v}_t^C $。

     $D$ 和 $U$ 表示 $ \mathbf{DOWN}$ 和 $\mathrm{UP}$ ,分别表示上采样和下采样

  2. KVCache 占用空间大幅下降（定性：缓存长的变成缓存短的，缓存两个变成缓存一个）：

     通过低秩压缩，将原本较长的 $ K $ 和 $ V $ 向量压缩为更短的表示，从而大幅减少 KV cache 的存储空间需求。

     缓存的长度从长变短，且只需缓存一个中间表示 $ \mathbf{c}_t^{KV} $ 而不是两个独立的 $ K $ 和 $ V $。

• 注意：上采样矩阵$ W^{UK} $ 和 $ W^{UV} $，可以融合到别的矩阵操作里面，也就是说不需要显式计算得到 $ \mathbf{k}_t^C $ 和 $ \mathbf{v}_t^C $，而可以直接从 基于压缩后的中间表示 ${\mathbf{c}}_t^{KV}$ 计算多头注意力，简化了计算流程。

  因为计算的时候甚至都不需要显式进行融合操作，而是由神经网络自动通过训练进行的，我们仅需要对压缩后的隐向量操作即可。
  $$\begin{gathered} q=W_1{h}_q \\ k=W_2{h}_k \\ {q}^{T}k=(W_1{h}_q{)}^T(W_2{h}_k)=h_q{W}_1{W}_2{h}_k=h_q(W_1{W}_2)h_k \end{gathered}$$

  计算时，可以提前先将两个矩阵先计算好相乘的结果，这样两个矩阵就被融合成了一个矩阵，可以直接由输入变量进行计算了，而不必得到中间的计算结果 $q$ 和 $k$。

  甚至在神经网络计算时，我们只需要声明一个中间矩阵就可以，神经网络通过训练会直接得到 $W_1{W}_2$ 的计算结果。所以在MLA计算过程中和代码中，根本没有 $W^{UK}$、$W^{UV}$ 这两个上采样矩阵，自动被融合在了 $W^Q$、$W^O$ 里面。

• 同时也压缩了query向量（为了对称美，为了能在同一个空间表示）

  不能直接在压缩后的向量上应用RoPE,因为压缩后的向量是经过矩阵融合后的结果，其结构和原始的查询向量或键向量已经发生了变化。直接在压缩后的向量上应用 RoPE，会导致以下问题：

  1. 位置信息丢失：RoPE 的设计初衷是通过旋转查询和键向量的不同部分来捕获位置信息。如果直接在压缩后的向量上应用，位置信息的旋转操作可能无法正确反映原始向量的位置关系。
  2. 计算不匹配：压缩后的向量与原始向量的维度和结构不同，直接应用 RoPE 可能会导致计算不一致或错误。

  那么可不可以在解压后的向量上应用RoPE呢？可以，但是影响效率，因为前面已经说过不用显示地计算解压后的向量，而是直接应用压缩后的向量。 如何解决呢？再造一个向量，单独应用RoPE，具体来说，可以将Query和Key向量分为两部分，一部分是压缩后的向量，另一部分是单独应用RoPE的向量。这样可以在保持计算效率的同时，准确地表示位置信息。具体公式如下：
  $$\begin{array}{rl}& \left[{\mathbf{q}}_{t,1}^R,{\mathbf{q}}_{t,2}^R,\dots ,{\mathbf{q}}_{t,n_h}^R\right]={\mathbf{q}}_t^R=\mathrm{RoPE}\left(W^{QR}{\mathbf{c}}_t^Q\right),\\ & {\mathbf{k}}_t^R=\mathrm{RoPE}\left(W^{KR}{\mathbf{h}}_t\right),\\ & {\mathbf{q}}_{t,i}=\left[{\mathbf{q}}_{t,i}^C,{\mathbf{q}}_{t,i}^R\right],\\ & {\mathbf{k}}_{t,i}=\left[{\mathbf{k}}_{t,i}^C,{\mathbf{k}}_t^R\right],\end{array}$$

  1. 计算带旋转位置编码的 Query
     $$[{\mathbf{q}}_{t,1}^R,{\mathbf{q}}_{t,2}^R,\dots ,{\mathbf{q}}_{t,n_h}^R]={\mathbf{q}}_t^R=\mathrm{RoPE}\left(W^{QR}{\mathbf{c}}_t^Q\right)$$

     • 输入：
       ${\mathbf{c}}_t^Q$ 是第 $t$ 个 token 的“内容向量”（即尚未加位置信息的原始 query 向量）。 $W^{QR}$ 是把 ${\mathbf{c}}_t^Q$ 映射成多头的线性变换矩阵（形状：$d_{\text{model}}\to n_h{d}_k$）。
     • RoPE（Rotary Position Embedding，旋转位置编码）
       把每个子向量 $(W^{QR}{\mathbf{c}}_t^Q{)}_i$ 乘以一个与绝对位置 $t$ 对应的旋转矩阵，得到一个带绝对位置信息的向量 ${\mathbf{q}}_{t,i}^R$。 整个多头结果拼在一起就是 ${\mathbf{q}}_t^R=[{\mathbf{q}}_{t,1}^R,\dots ,{\mathbf{q}}_{t,n_h}^R]$。

  2. 计算带旋转位置编码的 Key
     $${\mathbf{k}}_t^R=\mathrm{RoPE}\left(W^{KR}{\mathbf{h}}_t\right)$$

     • 与 Query 完全对称：

       ${\mathbf{h}}_t$ 是第 $t$ 个 token 的原始 key 向量；
       $W^{KR}$ 是映射矩阵；
       经过 RoPE 后得到的 ${\mathbf{k}}_t^R$ 也是多头形式，但这里把所有头拼在一起写成一个整体。

  3. 把 Query 拆成“内容+位置”两部分再拼接
     $${\mathbf{q}}_{t,i}=[{\mathbf{q}}_{t,i}^C,{\mathbf{q}}_{t,i}^R]$$

     • ${\mathbf{q}}_{t,i}^C$：第 $i$ 个头的“纯内容”向量
     • ${\mathbf{q}}_{t,i}^R$：刚才用 RoPE 得到的“位置”向量。
     • 把这两段向量沿最后一维拼接，得到最终用于注意力计算的 query 向量 ${\mathbf{q}}_{t,i}$。

  4. 把 Key 也拆成“内容+位置”两部分再拼接
     $${\mathbf{k}}_{t,i}=[{\mathbf{k}}_{t,i}^C,{\mathbf{k}}_t^R]$$

     • 与 Query 对称：
       ${\mathbf{k}}_{t,i}^C$ 是第 $i$ 个头的“纯内容” key。
       ${\mathbf{k}}_t^R$ 是共享的位置信息（所有头用同一位置编码，所以不再区分 $i$）。
     • 拼接后得到 ${\mathbf{k}}_{t,i}$。

  ---

代码

• 在这个视频中，作者给出了一个会比原论文图更直观的图，这个图更清晰一些

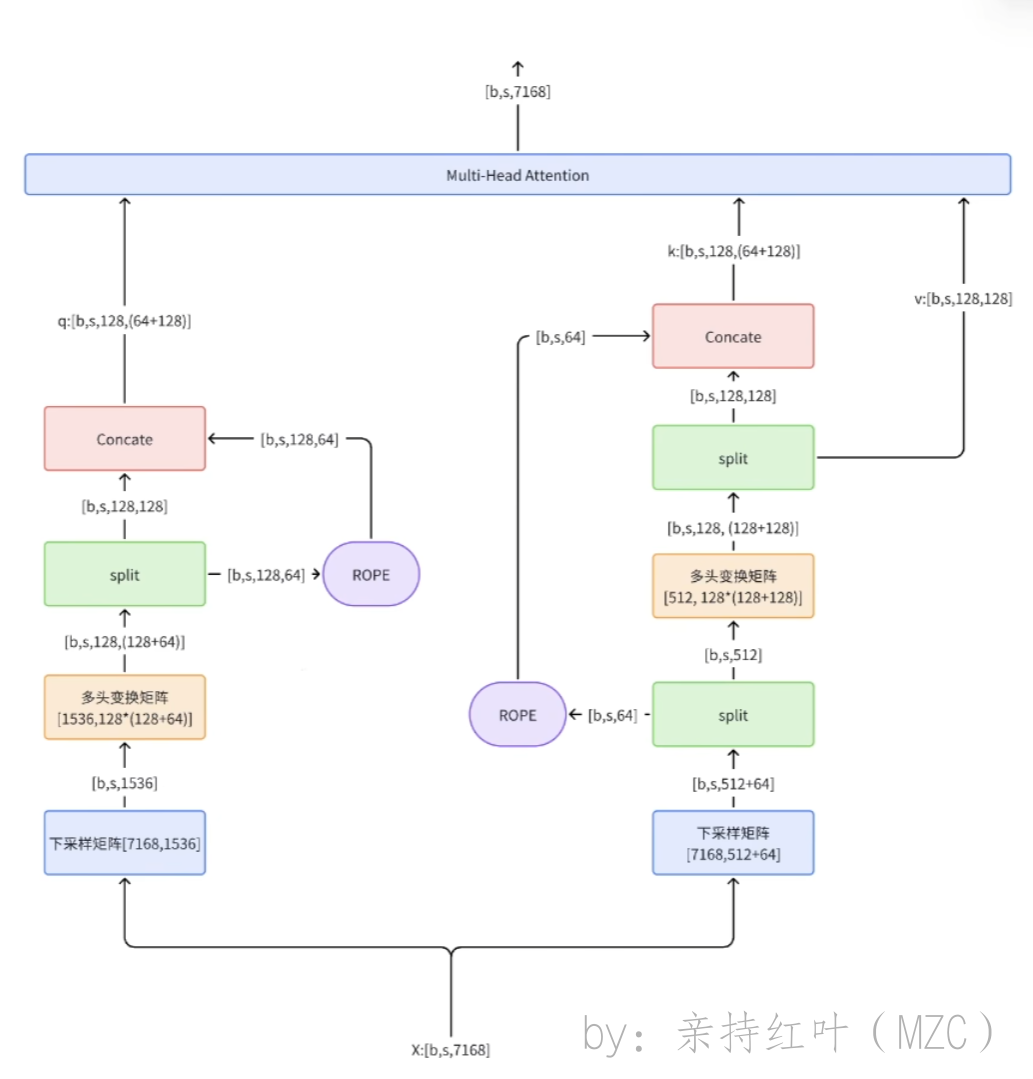
• 代码：

  from readline import append_history_file
  from torch import nn
  import torchclass MLA(nn.Module):def __init__(self):self.dim=7168self.n_heads = 128self.q_lora_rank = 1536 # q压缩后维度self.kv_lora_rank = 512 # kv压缩后维度self.qk_nope_head_dim = 128self.qk_rope_head_dim = 64self.qk_head_dim = self.qk_nope_head_dim + self.qk_rope_head_dim # 128+64self.v_head_dim = 128self.wq_a = nn.Linear([7168,1536]) # 下采样矩阵，得到压缩后的q向量self.wq_b = nn.Linear([512,128*(128+64)]) # 变换成多头注意力和用来旋转位置编码的向量self.wkv_a = nn.Linear([7168,64+512]) # 下采样矩阵，得到压缩后的kv向量self.wkv_b = nn.Linear(512,128*(128+128)) # 变换成多头注意力和用来旋转位置编码的向量self.wo = nn.Linear([128*128, 7168]) # 最后进行的投影层def forward(self,x):q = self.wq_b(self.wq_a(x))q = q.view(bsz,seqlen,128,128+64)q_nope,q_pe = torch.split(q,[128,64],dim=-1)q_pe = apply_rotary_emb(q_pe)kv = self.wkv_a(x) # [b,s,512+64]kv,k_pe = torch.split(kv,[512,64],dim=-1)k_pe = apply_rotary_emb(k_pe.unsqueeze(2))q = torch.cat([q_nope,q_pe],dim=-1)kv = self.wkv_b(kv)kv = kv.view(bsz,seqlen,128,128+128)k_nope,v = torch.split(kv,[128,128],dim=-1)k = torch.cat([k_nope,k_pe],dim=-1)self.k_cache[:bsz,...] = kself.v_cache[:bsz,...] = vscores = torch.einsum("bshd,bthd->bsht",q,self.k_cache[:bsz,:end_pos])x = torch.einsum("bsht,bthd->bshd",scores,self.v_cache[:bsz,:end_pos])x = self.wo(x.flatten(2))return x

总结

• MLA缓存的Latent KV比较短，相当于2.25个MQA的缓存量，但MLA有恢复全K、V的能力，表达能力比GQA，MQA要强，所以MLA能做到又快又省又强大。