当前位置：首页 > news >正文

数据结构——单调栈

news 2025/7/19 10:12:05

一、什么是单调栈？

单调栈是一种特殊的栈数据结构，它的特点是栈内的元素始终保持着某种单调性（递增或递减）。这种数据结构在解决一些数组相关的问题时非常高效，特别是涉及到 "下一个更大元素"、"上一个更小元素" 等场景。

单调栈的时间复杂度

由于每个元素最多入栈和出栈各一次，因此单调栈相关算法的时间复杂度通常为 O (n)，其中 n 是数组的长度，这比暴力解法的 O (n²) 效率高很多。

使用单调栈的关键在于理解何时需要弹出栈元素以及如何维护栈的单调性，根据具体问题可以选择维护递增栈或递减栈。

二、单调栈的实现过程

我们来手动模拟单调递增栈代码的执行过程，数组为 {3, 1, 4, 2, 5}，栈的初始状态为空：

步骤 1：处理第一个元素 `3`

栈为空，直接入栈
栈状态：[3]

步骤 2：处理第二个元素 `1`

当前元素 1 与栈顶元素 3 比较：1 < 3（满足递增条件）
直接入栈
栈状态：[3, 1]

步骤 3：处理第三个元素 `4`

当前元素 4 与栈顶元素 1 比较：4 > 1（不满足递增条件）
- 弹出 1，栈变为 [3]
继续比较：4 > 3（仍不满足递增条件）
- 弹出 3，栈变为空
栈为空，将 4 入栈
栈状态：[4]

步骤 4：处理第四个元素 `2`

当前元素 2 与栈顶元素 4 比较：2 < 4（满足递增条件）
直接入栈
栈状态：[4, 2]

步骤 5：处理第五个元素 `5`

当前元素 5 与栈顶元素 2 比较：5 > 2（不满足递增条件）
- 弹出 2，栈变为 [4]
继续比较：5 > 4（仍不满足递增条件）
- 弹出 4，栈变为空
栈为空，将 5 入栈
栈状态：[5]

最终结果

经过所有元素处理后，栈中元素为 [5]，保持了严格的单调递增特性。

如果要找原数列中第一个小于x的数，当x入栈时，栈里如果还有元素，该元素就是第一个小于x的数，如果没有，也就证明没有小于x的数

整个过程中，每当新元素破坏栈的递增性时，就弹出栈顶元素，直到栈重新满足递增条件后再将新元素入栈，这就是单调递增栈的核心工作原理。

#include <stack>
using namespace std;
void S() {stack<int> st;int nums[] = {3, 1, 4, 2, 5}; // 示例数据int len = sizeof(nums) / sizeof(nums[0]);//计算数组长度 for (int i = 0; i < len; i++) {int num = nums[i];while (!st.empty() && num >= st.top()) {st.pop();}st.push(num);}
}

三、如何判断是否需要使用单调栈？

需要为每个元素找到 “左边 / 右边第一个满足某种条件的元素”
例如：
- 下一个更大的元素（如 “数组中每个元素右侧第一个比它大的数”）；
- 上一个更小的元素（如 “每个元素左侧第一个比它小的数”）；
- 最近的边界（如 “柱状图中每个柱子左右能延伸到的最大范围”）。
示例场景：
经典的 “接雨水” 问题中，每个位置能接的雨水量取决于 “左侧最高柱子” 和 “右侧最高柱子”；“柱状图中最大矩形面积” 问题中，每个柱子的最大面积取决于 “左侧第一个更矮的柱子” 和 “右侧第一个更矮的柱子”—— 这些均属于 “找特定邻居” 的场景，适合用单调栈。

四、单调栈例题

B4273 [蓝桥杯青少年组省赛 2023] 最大的矩形纸片 - 洛谷

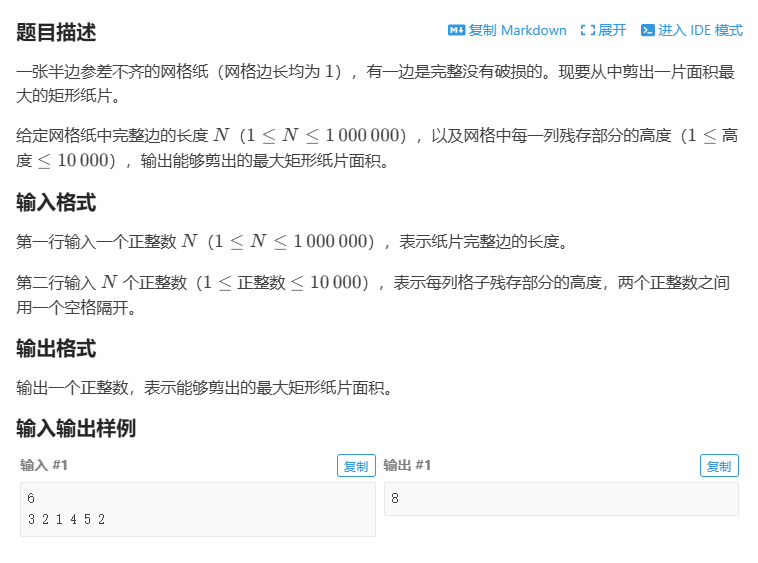
那么为什么需要使用单调栈呢？

对于每一列i（高度为h），其能形成的最大矩形的宽度，取决于：
左侧第一个高度小于h的列的位置（left）；
右侧第一个高度小于h的列的位置（right）。
此时宽度为right - left - 1，面积为h*(right-left-1)。

这正是单调栈的核心应用场景：为每个元素寻找 “左侧第一个更小元素” 和 “右侧第一个更小元素”（即 “前后特定邻居”）。

1.构建单调栈

while(!s.empty() && a[i]<s.top().h){//单调递增width=width+s.top().w;ans=max(ans,width*s.top().h);s.pop();}

while(!s.empty() && a[i]<s.top().h){
循环条件 —— 当栈不为空，且当前列的高度a[i]小于栈顶元素的高度时，执行循环。
（栈中存储的是 “高度” 和 “宽度” 信息，s.top().h表示栈顶元素的高度）
width = width + s.top().w：
累加宽度 —— 栈顶元素弹出前，将其宽度w累加到width中。
（这里的width代表 “当前可形成矩形的总宽度”，因为栈是单调递增的，弹出的元素高度都大于等于当前a[i]，可以合并计算宽度）
ans = max(ans, width * s.top().h)：
计算面积 —— 以栈顶元素的高度为矩形高度，以累加的width为宽度，计算面积，并更新最大面积ans。
s.pop()：
弹出栈顶元素 —— 因为当前元素a[i]比它矮，它的 “右侧边界” 已确定（就是i），后续不会再用到它，所以弹出。

AC代码

#include<bits/stdc++.h>
#define fo(i,a,b) for(int (i)=1;i<=(a);i+=(b))
using namespace std;
int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}// 栈中存储的元素结构：h表示高度，w表示该高度可向左延伸的宽度
struct node{int h,w;
};stack<node>s;               // 单调递增栈，用于维护高度的递增关系
long long a[1000001];       // 存储每列的高度，下标从1开始
long long ans=0;            // 记录最大矩形面积int main(){int n;n=read();                // 读取完整边的长度N// 读取每列的高度for(int i=1;i<=n;i++) a[i]=read();// 在数组末尾添加一个虚拟高度0，用于触发栈中所有元素的计算a[n+1]=0;// 遍历所有列（包括虚拟的n+1列）fo(i,n+1,1){long long width=0;   // 临时变量，累加当前可形成矩形的宽度// 核心逻辑：当栈非空且当前高度小于栈顶高度时，弹出栈顶并计算面积// 维持栈的单调递增特性while(!s.empty() && a[i]<s.top().h){// 累加弹出元素的宽度（这些元素高度都大于当前高度，可合并计算）width=width+s.top().w;// 计算以栈顶元素高度为矩形高度的最大面积，更新最大值ans=max(ans,width*s.top().h);// 弹出栈顶元素（其右侧边界已确定为当前i，无需保留）s.pop();}// 将当前高度入栈，宽度为累加的宽度+1（+1是当前列自身的宽度）s.push((node){a[i],width+1});}// 输出最大矩形面积cout<<ans<<endl;return 0;
}