算法学习笔记:29.拓扑排序——从原理到实战,涵盖 LeetCode 与考研 408 例题
拓扑排序(Topological Sorting)是一种针对有向无环图(DAG)的线性排序算法,它将图中的顶点按照一定规则排列,使得对于图中的任意一条有向边 u→v,顶点 u 都排在顶点 v 之前。拓扑排序在任务调度、课程安排、编译依赖等场景中有着广泛应用。
拓扑排序的基本概念与适用场景
核心定义
- 有向无环图(DAG):顶点间的边有方向,且不存在环路的图。拓扑排序仅适用于 DAG,若图中存在环,则不存在拓扑排序。
- 拓扑序:对于 DAG 中的顶点,存在一个线性序列 v₁, v₂, ..., vₙ,使得所有有向边 vᵢ→vⱼ 均满足 i < j。一个 DAG 可能存在多个拓扑序。
应用场景
- 任务调度:若任务 B 依赖任务 A,则 A 必须在 B 之前执行,拓扑排序可确定任务执行顺序。
- 课程安排:大学课程存在先修关系(如 “数据结构” 需先修 “C 语言”),拓扑排序可生成合理的选课顺序。
- 编译依赖:编译器处理源文件时,需按依赖关系(如头文件包含)确定编译顺序。
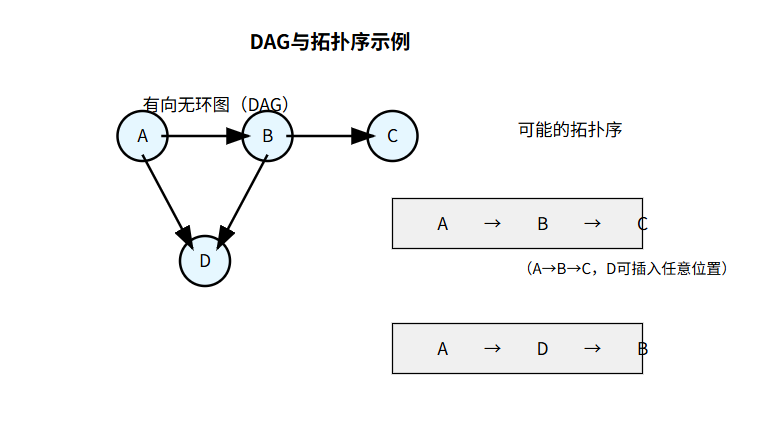
DAG 与拓扑序示例
拓扑排序的核心算法
Kahn算法(基于入度与队列)
核心思想:通过维护节点的入度(指向该节点的边数),逐步选出入度为0的节点(无前置依赖),并减少其邻接节点的入度,直至所有节点被处理或检测到环。
算法步骤
1. 计算入度:遍历图,记录每个节点的入度。
2. 初始化队列:将所有入度为0的节点加入队列。
3. 生成拓扑序:
- 出队一个节点,加入拓扑序。
- 对该节点的所有邻接节点,入度减1;若入度变为0,入队。
4. 检测环:若拓扑序长度小于节点总数,则图中存在环,无拓扑序。
基于DFS的拓扑排序
核心思想:通过深度优先搜索,在回溯时将节点加入拓扑序(逆后序遍历),若搜索中遇到回边(指向已访问但未回溯的节点),则存在环。
算法步骤:
1. 标记访问状态:用三个状态标记节点:未访问(0)、访问中(1)、已访问(2)。
2. 递归DFS:
- 若节点状态为访问中,检测到环。
- 若节点未访问,标记为访问中,递归遍历所有邻接节点。
- 回溯时,标记节点为已访问,加入拓扑序。
3. 逆序输出:拓扑序为逆后序遍历结果。
LeetCode例题实战
例题1:207. 课程表(中等)
题目描述:你这个学期必须选修 `numCourses` 门课程,记为 `0` 到 `numCourses - 1`。给你一个数组 `prerequisites`,其中 `prerequisites[i] = [ai, bi]`,表示在选修课程 `ai` 之前必须先选修 `bi`。判断是否可能完成所有课程的学习。
示例:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true(先学 0,再学 1)
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false(存在环 0→1→0)
解题思路(Kahn算法)
1. 构建图:用邻接表表示课程依赖关系,数组 `inDegree` 记录每个课程的入度。
2. 初始化队列:将入度为0的课程入队。
3. 拓扑排序:处理队列中的课程,减少依赖它的课程的入度,统计已处理课程数。
4. 判断结果:若已处理课程数等于 `numCourses`,则无环,可完成;否则有环,不可完成。
代码实现
import java.util.*;class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {// 1. 构建邻接表和入度数组List<List<Integer>> adj = new ArrayList<>();int[] inDegree = new int[numCourses];for (int i = 0; i < numCourses; i++) {adj.add(new ArrayList<>());}for (int[] p : prerequisites) {int course = p[0];int pre = p[1];adj.get(pre).add(course); // pre → courseinDegree[course]++;}// 2. 初始化队列(入度为0的课程)Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.offer(i);}}// 3. 拓扑排序int count = 0; // 已处理的课程数while (!queue.isEmpty()) {int curr = queue.poll();count++;// 处理依赖curr的课程for (int next : adj.get(curr)) {inDegree[next]--;if (inDegree[next] == 0) {queue.offer(next);}}}// 4. 判断是否所有课程都被处理return count == numCourses;}}复杂度分析
- 时间复杂度:O (V + E),V 为节点数(课程数),E 为边数(依赖关系数)。
- 空间复杂度:O (V + E),邻接表存储图,队列存储节点。
例题 2:210. 课程表 II(中等)
题目描述:同上题,但需返回一个可行的拓扑序;若无法完成所有课程,返回空数组。
示例:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,1,2,3] 或 [0,2,1,3] 等
解题思路
在 Kahn 算法中,将出队的节点依次加入拓扑序列表,最后若列表长度等于课程数则返回,否则返回空数组。
代码实现
import java.util.*;class Solution {public int[] findOrder(int numCourses, int[][] prerequisites) {// 1. 构建邻接表和入度数组List<List<Integer>> adj = new ArrayList<>();int[] inDegree = new int[numCourses];for (int i = 0; i < numCourses; i++) {adj.add(new ArrayList<>());}for (int[] p : prerequisites) {int course = p[0];int pre = p[1];adj.get(pre).add(course);inDegree[course]++;}// 2. 初始化队列Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.offer(i);}}// 3. 拓扑排序并记录结果List<Integer> topoOrder = new ArrayList<>();while (!queue.isEmpty()) {int curr = queue.poll();topoOrder.add(curr);for (int next : adj.get(curr)) {inDegree[next]--;if (inDegree[next] == 0) {queue.offer(next);}}}// 4. 检查是否有环if (topoOrder.size() != numCourses) {return new int[0];}// 转换为数组int[] result = new int[numCourses];for (int i = 0; i < numCourses; i++) {result[i] = topoOrder.get(i);}return result;}}复杂度分析
- 时间复杂度:O (V + E),同 Kahn 算法。
- 空间复杂度:O (V + E),额外存储拓扑序列表。
考研 408 例题解析
例题 1:概念辨析题(选择题)
题目:下列关于拓扑排序的叙述中,错误的是( )。
A. 拓扑排序仅适用于有向无环图(DAG)
B. 一个 DAG 的拓扑序是唯一的
C. Kahn 算法通过维护入度为 0 的节点生成拓扑序
D. 基于 DFS 的拓扑排序需检测回边以判断是否有环
答案:B
解析:
- A 正确:有环图不存在拓扑序。
- B 错误:一个 DAG 可能有多个拓扑序(如示例中的 A→B→C 和 A→D→B)。
- C 正确:Kahn 算法的核心是入度管理。
- D 正确:DFS 中遇到回边(访问中状态的节点)说明有环。
例题 2:算法设计题(408 高频考点)
题目:已知一个有向图用邻接表表示,设计一个算法判断该图是否为 DAG,若为 DAG 则输出其拓扑序,否则输出 “有环”。要求使用 Kahn 算法,并分析时间复杂度。
解题思路
- 数据结构:邻接表 adj 存储图,数组 inDegree 存储入度。
- 算法步骤:
- 计算所有节点的入度。
- 入度为 0 的节点入队,初始化拓扑序列表。
- 处理队列,更新入度和拓扑序,统计处理节点数。
- 若处理节点数等于总节点数,输出拓扑序;否则输出 “有环”。
代码实现
import java.util.*;public class TopologicalSort {// 判断是否为DAG并返回拓扑序,否则返回nullpublic List<Integer> isDAGAndTopoOrder(List<List<Integer>> adj, int n) {int[] inDegree = new int[n];// 计算入度for (int u = 0; u < n; u++) {for (int v : adj.get(u)) {inDegree[v]++;}}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < n; i++) {if (inDegree[i] == 0) {queue.offer(i);}}List<Integer> topoOrder = new ArrayList<>();while (!queue.isEmpty()) {int u = queue.poll();topoOrder.add(u);for (int v : adj.get(u)) {inDegree[v]--;if (inDegree[v] == 0) {queue.offer(v);}}}return topoOrder.size() == n ? topoOrder : null;}public static void main(String[] args) {// 示例:DAGint n = 4;List<List<Integer>> adj = new ArrayList<>();for (int i = 0; i < n; i++) {adj.add(new ArrayList<>());}adj.get(0).add(1);adj.get(0).add(2);adj.get(1).add(3);adj.get(2).add(3);TopologicalSort ts = new TopologicalSort();List<Integer> result = ts.isDAGAndTopoOrder(adj, n);if (result != null) {System.out.println("拓扑序:" + result); // 输出:[0,1,2,3] 或类似} else {System.out.println("有环");}}}复杂度分析
- 时间复杂度:O (V + E),V 为节点数,E 为边数。计算入度需 O (E),队列操作和入度更新共 O (V + E)。
- 空间复杂度:O (V + E),邻接表占 O (E),队列和拓扑序占 O (V)。
拓扑排序的扩展与应用
实际应用场景
- 项目管理:微软 Project 等工具用拓扑排序安排任务依赖关系。
- 编译系统:GCC 编译器处理源文件依赖,按拓扑序编译。
- 任务调度:操作系统进程调度中,按资源依赖关系确定执行顺序。
- 课程平台:MOOC 平台推荐先修课程,生成学习路径。
与其他图算法的关联
- 强连通分量(SCC):有环图的 SCC 可收缩为单个节点,形成 DAG 后再拓扑排序。
- 关键路径:在带权 DAG 中,拓扑序可高效计算最长路径(关键路径)。
- 最短路径:DAG 的单源最短路径可通过拓扑序在 O (V + E) 时间内求解。
考研 408 备考要点
- 核心考点:拓扑排序的适用条件、Kahn 算法步骤、环检测方法。
- 重点掌握:
- 邻接表的构建与入度计算。
- Kahn 算法中队列的作用及拓扑序生成逻辑。
- 拓扑排序与 DAG 的等价关系(存在拓扑序 ⇨ 是 DAG)。
- 常见错误:
- 忽略入度为 0 的节点初始队列可能为空(直接判定有环,但需确认节点数是否为 0)。
- 处理邻接节点时漏减入度,导致算法错误。
总结
拓扑排序是处理有向无环图(DAG)的核心算法,其 Kahn 算法和 DFS 算法各有优势:Kahn 算法直观易实现,适合求拓扑序;DFS 算法更简洁,适合环检测。本文通过 LeetCode 例题(课程表系列)展示了算法的实际应用,通过考研 408 例题巩固了理论基础,结合 SVG 图示清晰呈现了算法流程。
掌握拓扑排序的关键在于:
- 理解 DAG 与拓扑序的一一对应关系。
- 熟练实现 Kahn 算法的入度管理和队列操作。
- 能将实际问题抽象为 DAG,并用拓扑排序解决依赖关系问题。
在考研备考中,需重点关注算法的时间复杂度分析和环检测逻辑,这不仅是考试重点,也是解决复杂图问题的基础。
希望本文能够帮助读者更深入地理解拓扑排序算法,并在实际项目中发挥其优势。谢谢阅读!
希望这份博客能够帮助到你。如果有其他需要修改或添加的地方,请随时告诉我。

