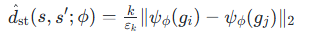【析精】Landmark-Guided Subgoal Generation in Hierarchical Reinforcement Learning

Landmark-Guided Subgoal Generationin Hierarchical Reinforcement Learning

基于地标指导的层次强化学习中的子目标生成

评价：

面对状态多变任务复杂奖励稀疏的环境，HRL是一个不错的选择。面对上层网络需要为下层网络输出子目标。因为会有了一个V（状态，子目标）的价值函数用于评估子目标的好坏。其次子目标的是如何设定的呢？在本文中根据覆盖度和新颖度设计了一批“地标“，也可以看作是子目标的候选集。通过最短路径的方法，获得最紧急而非距离最近的地标点，记为$l_t^{sel}$.它可能距离当前状态过远，直接作为子目标会导致低层策略难以达成。生成伪地标 $g_t^{pseudo}$，将其投影到当前状态的邻域.

策略模型分为高层策略和低层策略。两个模型都是TD3,独立参数不共享。高层策略输入状态$s_t$,输出子目标$g_t$，这里的子目标可分为绝对子目标和相对子目标。低层网络输入当前状态+子目标，输出原子动作a_t. 在奖励方面，低层网络获得即使奖励，而高层网络在时间m后获得轨迹奖励。低层是每步更新，高层是mod m=0的时候更新。

摘要

目标条件化的<font =color=blue>分层强化学习（hierarchical reinforcement learning，HRL）在解决复杂和长时程的强化学习任务方面显示出有希望的结果。然而，目标条件化HRL中高级策略的动作空间通常很大，因此导致探索不足，训练效率低下。
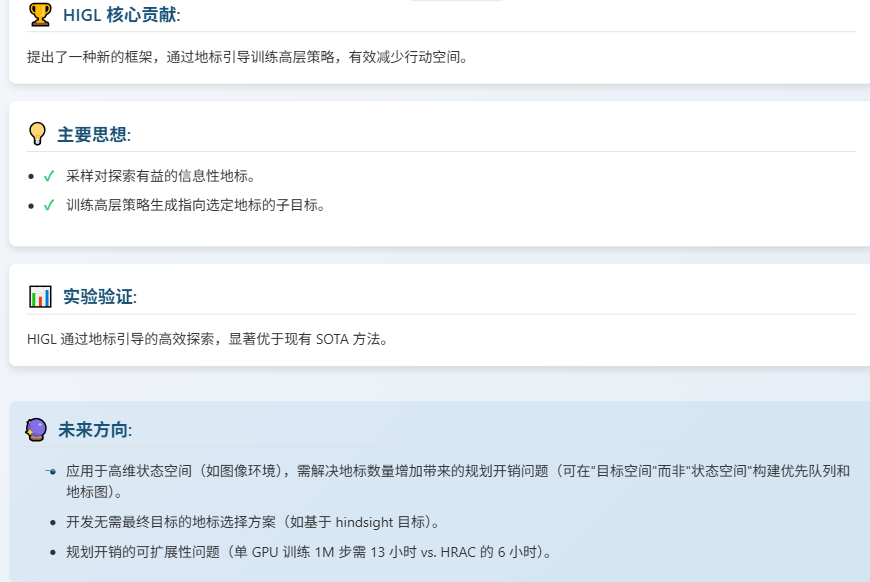
在本文中，我们提出了由地标引导的分层强化学习（ HIerarchical reinforcement learning Guided by Landmark,HIGL），这是一个新颖的框架，用于通过地标指导减少动作空间的高级策略训练，即探索有前景的状态。HIGL的关键组成部分是两部分：(a) 采样对探索有信息的地标和(b) 鼓励高级策略生成一个子目标以选择的地标为目标。(a)方面，我们考虑两个标准：覆盖整个已访问状态空间（即，状态的分散度）和状态的新颖性（即，状态的预测误差）。对于(b)，我们选择一个地标作为图中节点为地标的最短路径中的第一个地标。我们的实验表明，由于由地标引导的高效探索，我们的框架在各种控制任务上优于先前的技术。

一、背景

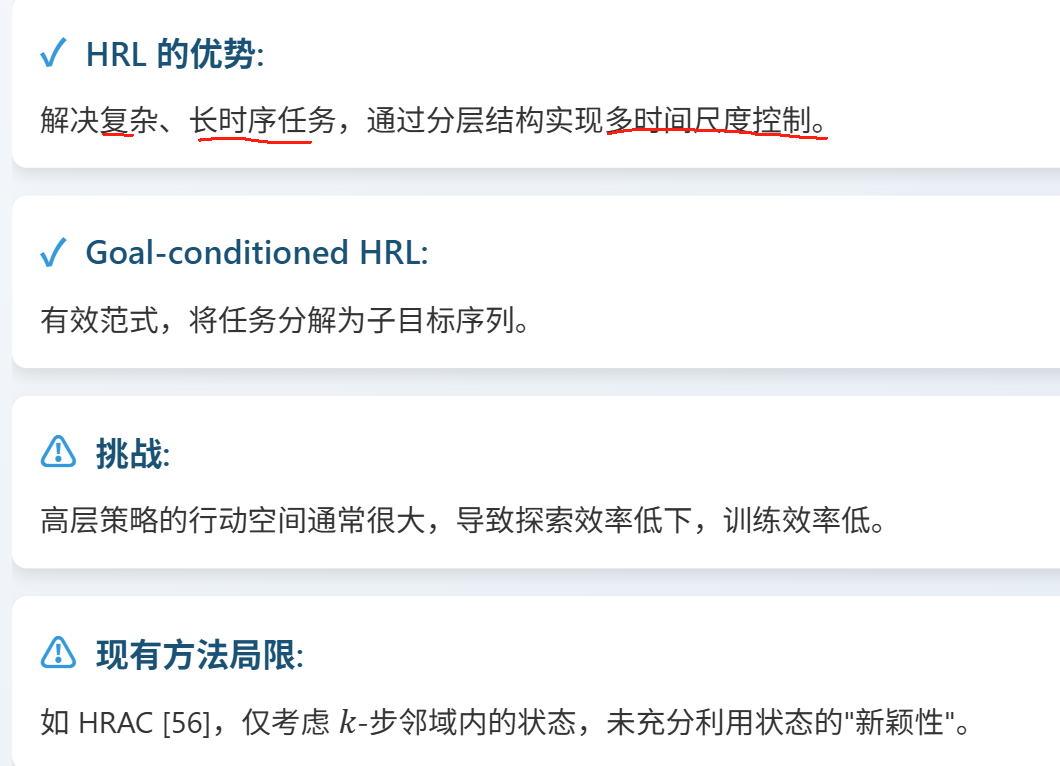
HRAC（Hierarchical Reinforcement Learning with Adjacency Constraint）是一种基于邻接约束子目标的分层强化学习算法，核心思想是把高层的子目标空间从整个状态空间限制到“当前状态 k 步可达的局部区域”，从而减少高层策略的探索难度，同时给底层策略提供更有效的学习信号

模块	说明
邻接约束（Adjacency Constraint）	高层策略只能输出当前状态 $s_t$ 的 k 步可达区域（如曼哈顿距离 k 以内的状态）作为子目标。
分层结构	高层策略 ${\pi }_h$ 选择子目标 $g_t\in \text{Adj}(s_t,k)$，底层策略 ${\pi }_l$ 执行原始动作达成 $g_t$。
优势	高层探索空间由全局 $\mathcal{S}$ 缩小到 $\text{Adj}(s_t,k)$，样本复杂度大幅降低。

与其他方法比较

方法	子目标空间	探索效率	典型场景
HIRO	全局状态空间	低（需探索整个空间）	连续控制
HAC	全局状态空间 + HER	中（利用后见经验）	稀疏奖励任务
HRAC	k 步邻接区域	高（局部探索）	迷宫、导航等离散/连续任务

1.1 HIGL核心思想：基于地标的引导

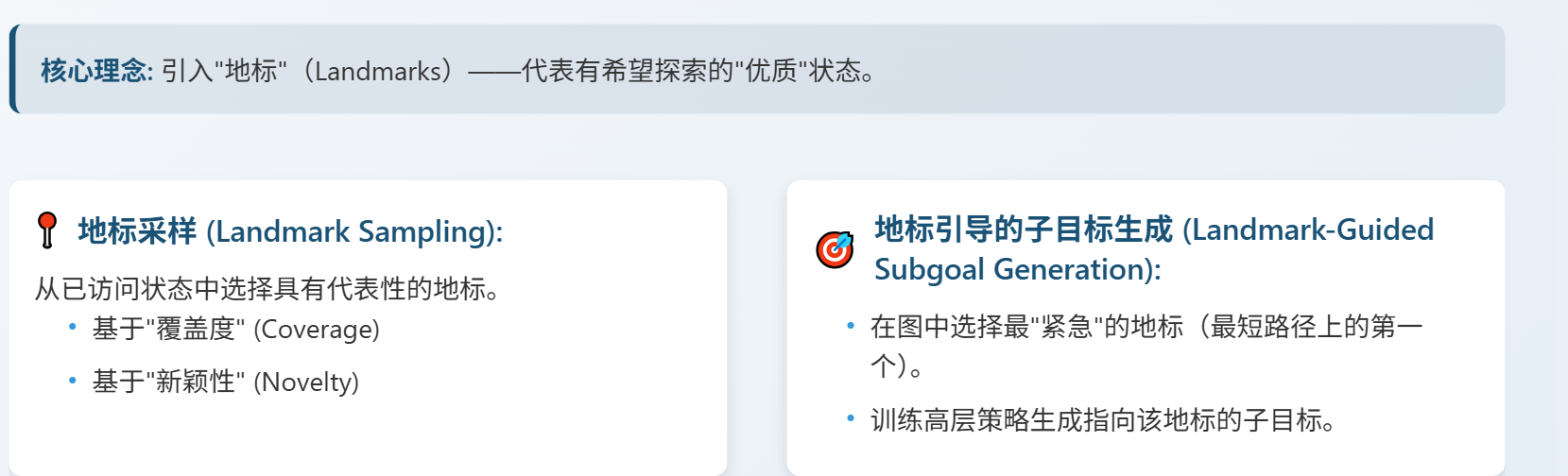
我们的核心想法很简单:与其让高层策略在茫茫状态空间中瞎转悠，不如给它指明几个有希望的路标，也就是我们说的地标。HIGL主要有两块关键内容

🍭第一，怎么采样这些地标?
我们考虑了两个标准:一是覆盖度，确保地标能代表已探索区域的广度;二是新颖性，鼓励探索那些没见过的新奇状态。

🍭第二，有了地标，怎么引导高层策略去生成子目标呢?
我们会构建一个图，把当前状态、目标和所有地标都放进去，然后用最短路径算法找出到达最终目标的第一站，也就是最紧急的那个地标。

接着，我们就训练高层策略，让它努力生成指向这个选定地标的子目标。

1.2 HIGL框架概览

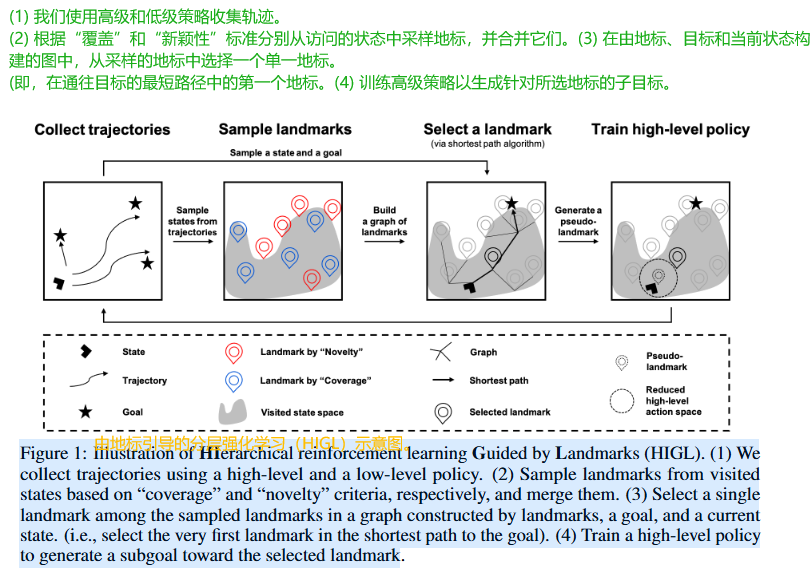
循环：

1. 轨迹收集: 使用高低层策略交互环境。

   智能体通过高阶和低阶策略在环境中跑起来，收集数据轨迹。

2. 地标采样: 基于"覆盖度"和"新颖性"标准，从访问过的状态中采样地标并合并。

   我们从这些轨迹里，根据前面说的覆盖度和新颖性标准，挑选出一批有代表性的地标，并把它们合并起来。
   覆盖度标准：使用 FPS 算法选择在状态空间中尽可能分散的地标，确保覆盖整个探索区域
   新颖性标准：基于RND预测误差选择新颖状态作为地标

3. 地标选择: 在由地标、目标和当前状态构建的图中，选择最短路径上的第一个地标作为下一个目标。

   接着，我们构建一个图，节点包括当前状态、最终目标以及我们选出来的所有地标。
   在这个图上，我们用最短路径算法，比如价值选代，来规划从当前状态到最终目标的最佳路径。

4. 高层策略训练: 训练高层策略生成指向所选地标的子目标

   我们选择这条路径上离当前状态最近的那个地标，作为下一个要引导的子目标。

通过不断地收集、采样、选择和训练，智能体就能越来越高效地完成任务了。

💡 既然有了最短路径算法，为啥还要采用人工智能的方法进行AI训练呢？

• 最短路径算法只能提供静态路径规划
• AI训练使高层策略能够：
  (1) 动态适应环境变化
  (2) 学习生成可达的子目标（通过伪地标机制）
  (3) 结合探索与利用的平衡
• 最终效果优于纯规划方法，如实验显示HIGL在Ant Maze任务中成功率65.1%，远高于HRAC的17.6%

二、Preliminaries

我们用有限时间、目标条件化的马尔可夫决策过程（MDP）[47]来表述控制任务，定义为一个元组$（\mathcal{S},\mathcal{G},\mathcal{A},p,r,\gamma ,H）$，其中S是状态空间，G是目标空间，A是动作空间，p (s′|s, a) 是转移动态，r (s, a) 是奖励函数，γ ∈ [0, 1) 是折扣因子，H 是时间范围。

2.1 Goal-conditioned HRL.

目标条件化的HRL。
我们考虑一个由两个层次组成的框架：高级策略$\pi (g|s;{\theta }_{high})$和低级策略$\pi (a|s,g;{\theta }_{low})$，其中每个策略分别由神经网络参数化，其参数分别为${\theta }_{high}$和${\theta }_{low}$。在每个时间步t，高级策略生成高级动作，即子目标$g_t\in \mathcal{G}$.要么 从其策略$g_t\sim \pi (g|s_t;{\theta }_{high})$中采样（当t≡0(mod k)时）。要么使用预定义的目标转移过程$g_t=h(g_{t-1},s_{t-1},s_t)$，即对于相对子目标方案[30,56]，$h(g_{t-1},s_{t-1},s_t)=g_{t-1}+s_{t-1}-s_t$；对于绝对子目标方案，$h(g_{t-1},s_{t-1},s_t)=g_{t-1}$。低级策略观察状态$s_t$和目标$g_t$，并执行低级原子动作$a_t\sim \pi (a|s_t,gt;{\theta }_{low})$。然后，高级策略的奖励函数如下所示为来自环境的m个外部奖励之和：

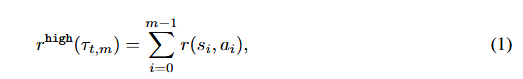
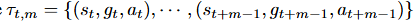表示大小为m的轨迹段。

策略执行频率：

• 高级策略：每m个时间步生成一次子目标（当t ≡ 0 mod m时）
• 低级策略：每个时间步t都生成原子动作

奖励机制流程：
a) 当t ≡ 0 mod m时：

• 高级策略生成子目标g_t
• 低级策略开始执行m步轨迹${\tau }_{t,m}=(s_t,g_t,a_t),...,(s_{t+m-1},g_{t+m-1},a_{t+m-1})$

b) 在t+m时刻：

• 计算这m步的环境奖励总和 $r^{high}({\tau }_{t,m})={\Sigma }_{i=0}^{m-1}r(s_i,a_i)$
• 该奖励作为高级策略在时间t决策的延迟奖励

组件	输入（Input）	输出（Output）	频率
高层策略	当前状态 $s_t$	子目标 $g_t$ （相对/绝对）	每 m 步
低层策略	当前状态 $s_t$ + 子目标 $g_t$	原子动作	每步（t）

在目标条件化分层强化学习（HRL）中， 相对子目标（Relative Subgoals） 和 绝对子目标（Absolute Subgoals） 是两种不同的设计范式，实际应用中通常需要根据任务特性选择其中一种，而非同时使用。以下是两者的对比和选择依据：

特性	相对子目标	绝对子目标
定义	指定相对于当前状态的偏移量（如“向右移动2米”）	指定全局坐标系中的目标（如“到达坐标(5,5)”）
高层策略输出	$g_t={\Delta }_s=s_{t+k}-s_t$	$g_t=s_{t+k}$（目标状态）
低层奖励函数	$r^{low}=-||\phi (s_{t+1}-s_t)-g_t||$	$r^{low}=-||\phi (s_{t+1}-g_t)||$
适用场景	动态环境、连续控制任务（如机器人运动）	静态环境、离散目标（如导航到固定点）
探索效率	更适应局部变化，适合长轨迹优化	更适合全局目标明确的场景
实现复杂度	需设计合理的偏移量约束	需确保目标在可达空间内

高级策略的目标是通过为低级策略提供与目标空间goal space$\mathcal{G}$中的距离成比例的内在奖励，来最大化$r^{high}$的期望总和。具体来说，在相对子目标方案[30, 56]中，低级策略的奖励函数定义为:

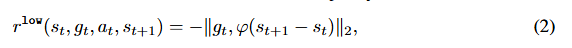
$\phi :\mathcal{S}\to \mathcal{G}$ :是一个将状态映射到目标的目标映射函数。相反，如果用绝对子目标方案替换，则奖励函数如下所示：

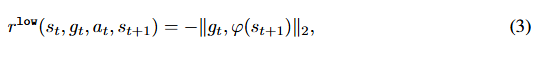
2.2 Random network distillation.

随机网络蒸馏。
探索算法的一行引入了状态的新颖性，这是通过 预测误差(prediction errors)[ 3, 14, 36, 41 ]、访问计数(visit-counts )[ 2, 35, 49]或状态熵估计(state entropy estimate)[ 13, 20, 29, 42]计算的。一个众所周知的方法是随机网络蒸馏（Random network distillation,RND）[ 3]，它使用神经网络的预测误差作为新颖性得分。具体来说，设$f$是一个具有固定参数$\bar{\theta }$的神经网络，而$\hat{f}$是由θ参数化的神经网络。RND通过最小化f的预期均方预测误差 ${\mathbb{E}}_{s\sim \mathcal{B}}\Vert \hat{f}(s;\theta )-f(s;\bar{\theta }){\Vert }_2$ 来更新θ。然后，将状态s的新颖性得分定义为：

对于与预测网络θ训练时所使用的状态不同的新奇状态，新颖性得分n(s)可能更高。

2.3 Adjacency network.

邻接网络。
设$d_{st}(s,s\prime )$是从状态s到状态s′的最短转移距离，即$d_{st}(s,s\prime )$是最佳代理从s到达s′所需的期望步数。为了估计$d_{st}$，张等人引入了一个由参数φ定义的邻接网络ψ，该网络区分两个状态是否为k步相邻。[56] 张等人介绍了一个邻接网络ψ，其参数化为φ，用于区分两个状态是否为k步相邻。该网络通过最小化下面的 对比式损失contrastive-like loss 来 学习从目标空间到邻接空间的映射：

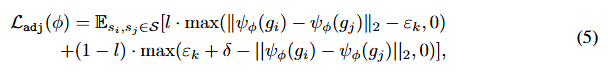
其中$\delta >0$是嵌入之间的边缘，${\epsilon }_k$是一个缩放因子，而l∈{0,1}l∈\{0,1\}l∈{0,1}表示从存储探索状态的邻接信息的k步邻接矩阵M中导出的k步邻接性标签。方程(5)对相邻状态嵌入$(l=1)$惩罚较大的欧几里得距离，而非相邻状态嵌入$(l=0)$则惩罚较小的欧几里得距离。然后可以估计最短转移距离如下：

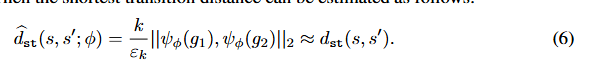
💡 状态$s,s^{\prime }$的维度不唯一，是仅靠位置分量计算状态之间的距离吗？
在HIGL框架中，邻接网络（Adjacency Network）估计的状态间距离 $d_{st}(s,s^{\prime })$ 并非仅基于位置分量计算，而是通过以下方式处理多维状态特征.
(1)邻接网络的核心设计
邻接网络 ${\psi }_{\varphi }$ 是一个神经网络，其输入是目标空间 $\mathcal{G}$ 的嵌入（而非原始状态空间 $\mathcal{S}$），输出是用于距离度量的低维嵌入。具体流程：

1. 状态到目标的映射：
   通过函数$\phi :\mathcal{S}\to \mathcal{G}$ 将状态 s 映射到目标空间 $g=\phi (s)$。
   例如：在Ant Maze中，$\phi (s)$ 可能提取 (x,y)坐标；在机械臂任务中可能提取末端执行器位置。
2. 目标空间的距离估计：
   邻接网络计算两个目标 $g_i,g_j$的嵌入距离：
   
   其中 通过对比学习优化（公式5），迫使相邻状态（k-步可达）的嵌入距离趋近于 ${\epsilon }_k$ 。

(2)多维状态特征的处理
若状态 s 包含位置以外的特征（如速度、传感器数据等），HIGL通过以下方式解决：

• 特征选择：
  映射函数 $\phi$通常手动设计或自动学习，仅提取与任务相关的关键特征。
  例如：在Ant Maze中，即使状态包含关节角度、速度，$\phi$ 可能仅保留 坐标。
  学习方案：若使用自动编码器学习 $\phi$，可通过辅助目标（如重构损失）约束嵌入空间。
• 距离的语义性:
  邻接网络的距离反映的是控制相关性（如可达性），而非纯几何距离。
  两个状态若在动力学上容易相互转移（如相邻位置且速度方向一致），即使几何距离较远，也可能被判定为“邻接”。

(3)与低级策略的协同
低级策略的价值函数 $V(s,g)$进一步修正距离估计：

• 在构建地标图时，边权重为 : $V(s_1,\phi (s_2-s_1))$（相对子目标）或 $V(s_1,\phi (s_2))$（绝对子目标）。

三、HIGL

3.1 地标采样

Coverage-based sampling基于覆盖的采样。

我们提出从重放缓冲区( replay buffer)$\mathcal{B}$中采样覆盖广泛访问状态的地标。为此，我们利用最远点采样（Farthest Point Sampling,FPS）[51]，它从B中采样一个状态池，并选择在该池中尽可能远离彼此的状态。具体来说，我们通过应用 FPS 来采样一组基于覆盖的地标Lcov={licov}iMcov=1L^{cov} = \{l^{cov}_i\}^{Mcov}_i=1Lcov={licov​}iMcov​=1，在目标空间中测量两个状态s和s′之间的距离为$||\varphi (s)-\varphi (s\prime )|{|}_2$，遵循黄等人。[15]。我们注意到 FPS 隐式地在已访问状态空间的前沿采样状态，这意味着基于覆盖的地标也隐含着值得探索的有希望的状态（参见图6以获得支持的实验结果）。

这里的距离不是直接在状态空间算，而是在一个叫做目标空间的映射空间里计算，用的是欧氏距离。这种方法的好处是，它能自动帮你找到那些位于已探索状态空间边界的点，这些点往往意味着新的可能性，或者说，它们本身就可能是一些不错的探索方向。

Novelty-based sampling.基于新颖性的采样。

为了显式地采样新地标，我们提出在环境交互过程中存储遇到的新状态并将其用作地标。为此，我们引入了一个固定大小为K的优先队列priority queue Q，其中每个元素（状态）的优先级定义为(4)中的状态n(s)的新颖性；队列将状态s以n(s)的优先级存储在Q中。这里的一个重要问题是，随着探索的进行，状态s的新颖性会降低，因此Q中存储的状态的优先级应不断更新。因此，我们提出了一种基于相似度的更新方案，该方案丢弃与新遇到的状态相似的先前存储样本。具体来说，当我们遇到一个状态s时，我们测量s在所有已存储状态s’ ∈ Q之间的相似度，并丢弃相似状态，即{s′∈Q:∣∣ϕ(s)−ϕ(s′)∣∣2<λ}\{s' ∈ Q : ||ϕ(s) − ϕ(s′)||_2 < λ\}{s′∈Q:∣∣ϕ(s)−ϕ(s′)∣∣2​<λ}，其中λ是相似度阈值。然后我们将一个状态s存储在Q中，并从Q中采样一组新颖性基地标记Lnov={linov}iMnov=1L^{nov} = \{l^{nov}_i \}^{Mnov}_i=1Lnov={linov​}iMnov​=1。

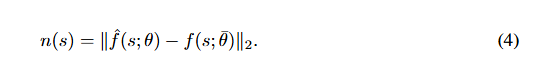
每个状态进入这个队列Q时，都有一个优先级，这个优先级就是它的新颖性得分n(s)，我们用的是 RND 随机网络蒸馏的方法来衡量这个得分。当智能体遇到一个新的状态s时，我们会先检查一下队列里有没有跟它长得太像的家伙，也就是相似度低于某个阈值入的状态。

💡 Why ?在HIGL框架中，新颖性采样只与优先级队列 Q中的状态比较（而非所有历史状态）

1. 计算效率的优化,复杂度降低：与所有历史状态比较（可能达数百万次）的复杂度是 $O(N)$，而与固定大小 的队列比较复杂度是 $O(1)$.
2. 避免重复存储相似状态.优先级队列的淘汰机制：队列 Q 是一个最大堆，始终保留当前最新颖的 K个状态。当新状态 s 比队列中最不新颖的状态更独特时，才会替换它。
3. 动态适应探索进展

• 新颖性的相对性：
  随着训练进行，早期新颖的状态可能变得普通。队列机制通过动态更新，始终反映当前最值得探索的区域。
  例子：在迷宫任务中，起点附近的状态在训练后期不再新颖，会被自动移出队列。
• RND的配合：
  队列中状态的优先级由RND预测误差 决定，误差越大越新颖。队列更新时：
  • 移除相似旧状态（基于状态嵌入距离）
  • 插入新状态（基于RND误差）.这种双重标准确保地标同时满足：
    空间分散性（覆盖度）
    时间新颖性（预测误差）

3.2 地标选择

构建一个图。

对于地标选择，我们构建一个图，其节点包括当前状态$s_t$、（最终）目标g 和地标L。🐸首先，我们将所有节点连接起来，并为每条边分配一个权重，该权重由两个节点之间的距离估计值函数V(s, g)给出，即对于相对子目标方案中的状态$s_1、s_2$，有$-V(s_1,\varphi (s_2-s_1))$，遵循先前的工作[9,15,34]。由于通过价值函数的距离估计是局部准确的，但对于远状态来说不可靠，因此我们遵循Huang等人，在相应边的权重大于预设阈值${\gamma }_{dist}$时断开两个节点。[15].

规划。在构建图之后，我们运行最短路径规划算法以从当前状态$s_t$选择访问的最紧急的状态$l_t^{sel}$到目标$g$。由于一般价值迭代对于RL问题恰好是图上的最短路径算法，因此我们利用价值迭代作为最短路径规划，遵循黄等人先前的工作。[15].通过选择到达目标的最短路径中的第一个地标，HIGL可以专注于最紧急的地标，忽略可能与从当前状态到达目标无关的地标。

3.3 训练高层策略：伪地标

我们选出了最紧急的地标$l_t^{sel}$。但是，直接用这个原始的地标去训练高层策略可能会有问题。这个地标可能是离当前状态st很远的，如果高层策略直接生成一个指向那么远地方的子目标，那低层策略可能根本没法一步到位，生成的子目标可能就是不可达的。这会导致低层策略收不到有效的奖励信号，学习就慢了。 为了解决这个问题，我们引入了一个巧妙的概念，叫做伪地标 Pseudo-landmark，记作${\hat{g}}_t^{pseudo}$。它的位置不是直接用选定的地标$l_t^{sel}$，而是在当前状态$s_t$和选定地标$I_t^{sel}$之间找一个中间点。 这样一来，我们生成的伪地标既不会离当前状态太远，保证了可达性，又大致指向了那个有希望探索的原始地标方向。

3.4 训练高层策略：地标损失

有了伪地标，我们怎么让高层策略去生成接近它的子目标呢?
我们设计了一个叫做地标损失 Landmark Loss 的东西，记作L landmark。这个损失函数的作用就是惩罚那些生成的子目标$g_t$离我们的伪地标${\hat{g}}_t^{pseudo}$ 太远的情况。

具体怎么衡量远不远呢?
我们用到了之前提到的邻接网络${\psi }_{\varphi }$。 这个网络可以判断两个目标在目标空间里是不是相邻的. 我们的地标损失就是计算生成的子目标$g_t$和伪地标${\hat{g}}_t^{pseudo}$ 经过${\psi }_{\varphi }$ 映射后的向量距离，如果这个距离 个阈值${\epsilon }_k$，就产生损失。注意，这里我们用的是一个非严格的约束，也就是 $max(.,0)$，这样可以避免训练过程过于不稳定。我们把这个地标损失$L_{landmark}$加入到原来高层策略的损失函数里，用一个系数$\eta$ 来平衡它和原来的目标奖励。 这样，高层策略在学习的同时，也会受到这个损失的引导，努力生成更靠近伪地标的子目标。至于低层策略，我们保持不变，按原来的方式训练就行。

四、实验

在本节中，我们设计实验以回答以下问题：

• HIGL如何与最先进的HRL方法[56]在各种长时连续控制任务（见图3）上进行比较？
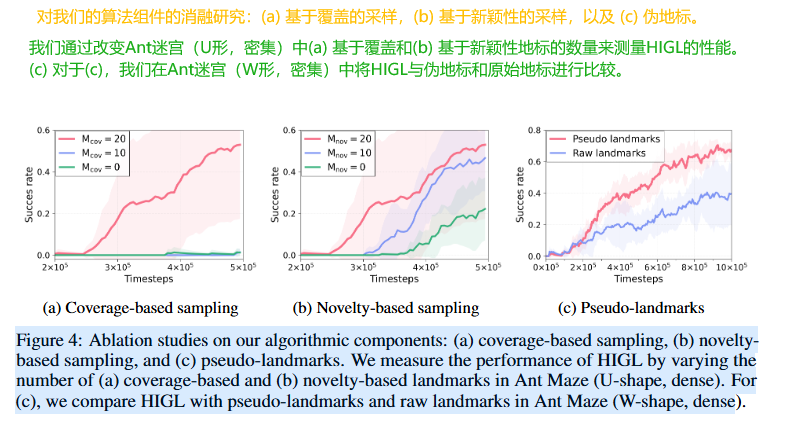
• 标志采样的覆盖范围和新颖性如何分别提高性能（见图4a，4b）？
• 伪地标如何影响性能，而不是使用原始选定的地标（见图4c）？
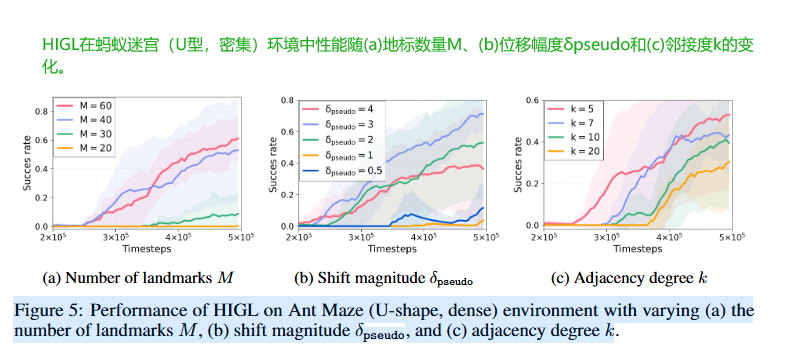
• 如何设置超参数：（1）地标数量M，（2）位移幅度δpseudo和（3）邻接度k如何影响性能（见图5a、5b、5c）？

4.1 实验设置：环境

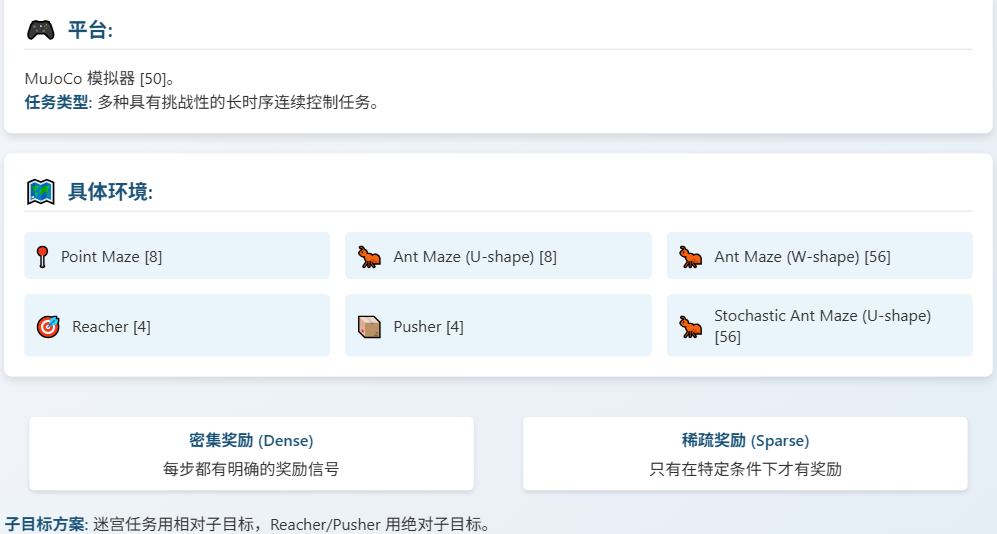
我们测试了 HIGL 在一系列具有挑战性的连续控制任务上的表现，包括经典的 Point Maze和 Ant Maze，有U型的也有 W 型的，还有 Reacher 和 Pusher 这两个机械臂任务。为了增加难度，我们还使用了带有随机噪声的 Stochastic Ant Maze。在奖励设置上，我们考察了密集奖励和稀疏奖励两种情况。密集奖励每一步都有反馈，而稀疏奖励只有在非常接近目标时才有奖励，这对探索能力要求更高。对于子目标方案，迷宫任务我们用了相对子目标，而 Reacher 和 Pusher 这种需要精确控制位置的任务，我们用了绝对子目标。

4.2 实验结果：与 SOTA 方法对比

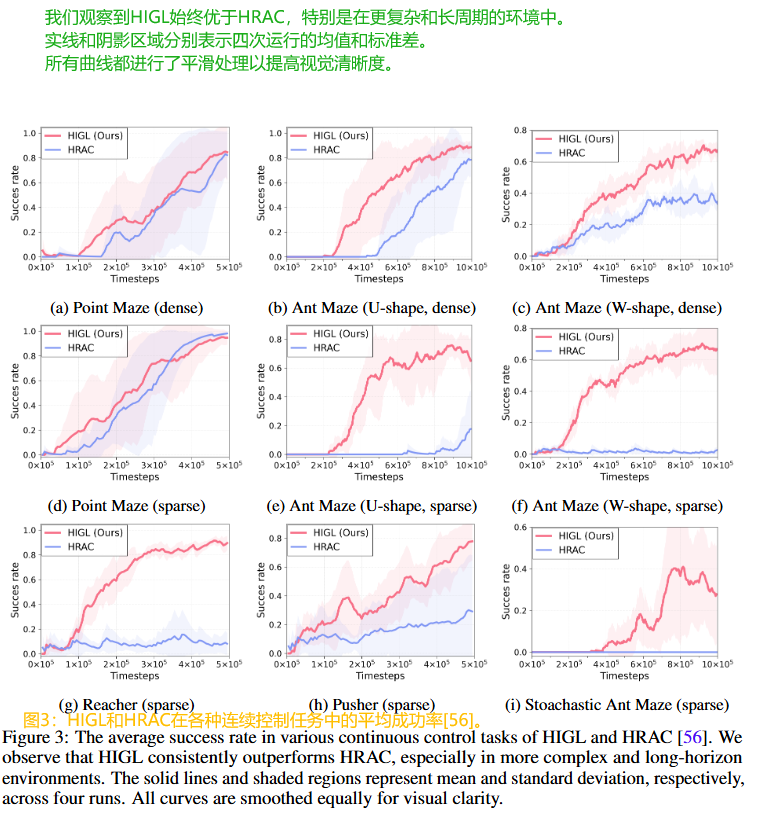
结论:
HIGL 在所有任务中均优于 HRAC，尤其在更复杂和长时序环境中优势明显。

原因分析:

• HIGL 考虑了状态的可达性和新颖性，而 HRAC 对所有邻近状态一视同仁。
• HIGL 通过规划识别出有希望探索的方向，并训练高层策略生成指向该方向的子目标。

显著提升: 例如，在 Ant Maze (U-shape, sparse) 任务中，HIGL 达到 65.1% 成功率，而 HRAC 仅为 17.6%。
鲁棒性: HIGL 在随机环境中也表现更好，且无需修改即可适用。

5.3 消融研究

组件有效性分析

• 覆盖度采样 (图4a):
  使用覆盖度地标对性能有积极影响。它们作为通往新状态或本身就是有希望状态的路标。

• 新颖性采样 (图4b):
  利用新颖性采样同样提升了性能。例如，仅使用 10 个新颖性地标就显著优于不使用。

• 伪地标 (图4c):
  与直接使用原始选定地标相比，使用伪地标能获得更好的性能。因为伪地标同时满足"可达"和"指向有希望探索方向"两个特性。

超参数影响

• 地标数量 M (图5a):
  增加地标数量通常能提高性能，因为能包含更多环境信息，且使图规划更可靠。

• 偏移量 ${\delta }_{pseudo}$ (图5b):
  偏移量影响伪地标的位置。太小则高层策略倾向于生成靠近当前状态的子目标；太大则可能导致生成不可达的子目标，性能下降。

• 邻接度 k (图5c):
  调整邻接度对超越 HRAC 的性能影响不大。但设置过大不合适，因为允许生成离伪地标很远的子目标，可能位于不可达区域。

4.4 定性分析：地标采样效果

• 覆盖度地标 (蓝点) 分散在已访问状态空间中。
• 新颖性地标 (红点) 集中在已访问空间的边界，这表明它们可能具有新颖性。
• 训练初期，由于智能体从左下角开始，覆盖度地标也集中在左下角。
• 随着训练进行，智能体探索范围扩大，覆盖度地标也更分散。
• 新颖性地标在整个训练阶段都集中在边界。

五、讨论与结论

六、HIGL 算法

6.1 算法输入与初始化

变量	输入参数
h	子目标转换函数（相对/绝对方案）
φ	状态到目标空间的映射函数
m	高层策略动作频率（每m步生成子目标）
N	总训练步数
C	邻接网络更新频率
$\mathcal{B}$	回放缓冲区
B	训练批次大小
M_cov, M_nov	覆盖/新颖性地标数量

初始化：

1. 策略网络：

• 高层策略 π_high：TD3算法，输出子目标 g_t
• 低层策略 π_low：TD3算法，输出原子动作 a_t

2. 辅助网络：

• 邻接网络 ${\psi }_{\phi }$：估计状态间可达性
• RND网络 $(f,\hat{f})$：计算状态新颖性 $n(s)=||\hat{f}(s)-f(s)||$

3. 存储结构：

• 回放缓冲区 $\mathcal{B}$：存储轨迹 $(s_t,a_t,r_t,s_{t+1})$
• 优先级队列 Q：维护高新颖性状态（最大堆，容量 K）

6.2 主训练循环（行3-24）

1. 环境交互阶段（行4-14）

(1) 子目标生成：

• 每 m 步（t % m == 0时）：
  • 高层策略生成子目标 $g_t\sim {\pi }_{high}(s_t)$
• 非 m 步时：
  • 使用转换函数 $g_t=h(g_{t-1},s_{t-1},s_t)$ 调整子目标
    相对方案：$g_t=g_{t-1}+(s_{t-1}-s_t)$
    绝对方案：$g_t=g_{t-1}$

(2) 动作执行与存储：

• 低层策略执行 $a_t\sim {\pi }_{low}(s_t,g_t)$
• 环境返回 $(s_{t+1},r_t)$，存入 $\mathcal{B}$
• 计算新颖性 n(s_t) 并更新队列 Q：
  若 n(s_t) 高于 Q 中最小值或存在相似状态（$||\phi (s_t)-\phi (s^{\prime })||<\lambda$），替换旧状态

2. 训练阶段（行15-23）

(1)地标采样（行16）：

• 覆盖性地标：从 B 中通过FPS算法采样 M_cov 个分散状态
• 新颖性地标：从 Q 中取 M_nov 个高新颖性状态
• 合并地标集 L = $L_{cov}\cup L_{nov}$

(2)地标选择与伪目标生成（行17-18）：

• 构建地标图：节点为 $s_t,g,L$，边权重通过低级价值函数 V(s, g) 计算
  最短路径规划选择最紧急地标 $l_t^{sel}$，生成伪目标：
  ${\hat{g}}_t^{pseudo}=\phi (s_t)+{\delta }_{pseudo}\cdot \frac{\phi (l_t^{sel})-\phi (s_t)}{||\phi (l_t^{sel})-\phi (s_t)||}$

(3)策略更新（行19-21）：

• 高层策略：
  优化TD3损失 + 地标损失 $L_{landmark}=max(||\psi (\phi (g_t))-\psi (\phi ({\hat{g}}_t^{pseudo}))||-{\epsilon }_k,0)$
  目标：使生成子目标 g_t 靠近伪目标
• 低层策略：
  标准TD3更新，奖励为子目标距离 -||φ(s_{t+1}) - g_t||$

(4)辅助网络更新（行22-23）：

• 每 C 步更新邻接网络 ψ_φ：
  从 B 采样状态对，用对比损失（公式5）优化 k-步可达性估计
• RND网络 f̂ 持续更新以最小化 ||f̂(s) - f(s)||

3. 关键设计分析

(1)地标机制的协同作用

• 覆盖性采样：确保地标覆盖已探索区域，避免遗漏。
• 新颖性采样：引导探索前沿，突破局部最优。
• 动态平衡：实验显示 M_cov = M_nov = 20 时效果最佳（Ant Maze）。

(2) 伪目标的必要性

• 解决可达性问题：原始地标可能过远（如 $l_t^{sel}$在迷宫另一端），伪目标将其投影到当前状态的邻域（${\delta }_{pseudo}$控制步长）。
  实验验证：图4c显示使用伪目标比原始地标成功率提升 >20%。

(3) 延迟奖励与分层训练

• 高层奖励延迟：每 m 步获得累计奖励，迫使高层学习长期规划。
• 低层即时反馈：每个时间步基于子目标距离调整，保证局部收敛。

4. 实现细节与超参数

(1)网络架构：

• 策略网络：3层MLP（300-300隐藏单元，ReLU）
• 邻接网络：4层MLP（128-128隐藏单元，输出32维嵌入）

(2)超参数：

• m = 20（Ant Maze），m = 5（Reacher）
• ${\delta }_{pseudo}=2.0$（迷宫），1.0（机械臂）
• λ = 0.1（相似性阈值），ε_k = 1.0（邻接尺度）

(3)训练加速：

• 早期阶段（前60k步）禁用伪目标（${\delta }_{pseudo}=0$），避免不准确规划干扰。

5. 与其他HRL方法的对比优势

模块	HIGL	传统HRL（如HRAC）
动作空间	地标引导的降维空间	原始子目标空间或固定邻域
探索效率	覆盖+新颖性双重引导	仅依赖随机探索或邻域采样
奖励设计	高层：延迟累计奖励 + 地标损失	高层：稀疏环境奖励
计算开销	需维护地标图和RND网络	仅需邻接网络

6. 局限性

• 规划成本：地标图最短路径搜索增加约50%训练时间（对比HRAC）。
• 状态依赖性：依赖 φ 的设计，若目标空间映射不佳（如高维图像），性能下降。

6.3 高层策略网络的优化

(1)优化目标：

• 主目标：最大化环境奖励的累计和（稀疏、长周期奖励）。
• 辅助目标：通过地标损失（Landmark Loss）引导子目标靠近伪地标（${\hat{g}}_t^{pseudo}$ ）

(2)优化步骤：

• 数据收集：
  高层每 m 步生成子目标 ，低层执行 m步轨迹
  存储轨迹及累计奖励 $r^{high}({\tau }_{t,m})$ 到回放缓冲区 $\mathcal{B}$

• 奖励计算：
  环境奖励：直接使用累计奖励 $r^{high}({\tau }_{t,m})$ （稀疏信号）。
  地标损失：$\mathcal{L}=\max (||{\psi }_{\varphi }(\phi (g_t))-{\psi }_{\varphi }(\phi ({\hat{g}}_t^{pseudo}))|{|}_2-{\epsilon }_k,0)$
  ${\psi }_{\varphi }$：邻接网络，衡量子目标与伪地标的可达性距离 .
  ${\epsilon }_k$：邻接阈值（超参数）

(3)策略更新：

• 使用TD3算法优化高层策略，总损失函数为：$\mathcal{L}=-\mathbb{E}[\gamma r^{high}({\tau }_{t,,}-\eta {\mathcal{L}}_{landmark})]$
  $\eta$ 平衡系数（默认 =20）。
• 地标损失作为正则项，约束子目标生成方向。

(4) 伪代码对应：

# 高层策略更新
high_loss = -td3_reward + eta * landmark_loss
high_policy.update(high_loss)

6.4 低层策略（Low-level Policy, ）的优化

(1)优化目标：最小化当前状态与子目标的距离（稠密、即时奖励）。

(2)优化步骤：

1. 数据收集：

• 每个时间步 t，低层策略根据当前状态 $s_t$和子目标 $g_t$生成动作 $a_t$ 。
• 存储转移 $(s_t,g_t,a_t,s_{t+1})$ 到 $\mathcal{B}$。

2. 奖励计算：

• 相对子目标：$r^{low}$
• 绝对子目标：$r^{high}$

3. 策略更新：

• 使用标准TD3算法优化，最大化 $r^{low}$ 。
• 无辅助损失：低层仅需拟合子目标，无需地标引导。

(3)伪代码对应：

# 低层策略更新
low_loss = -low_level_reward
low_policy.update(low_loss)