string + 栈 bitset 可达性统计（拓扑排序）

很多做题的时候宁愿想到用暴力模拟半天愣是想不到可以用栈来解决！

所以今天就加深对栈的印象，顺便熟悉一下string的一些相关操作（便于明年天梯赛的暴力模拟）。

string + 栈：

最优屏障

详解见代码：

// Problem: 最优屏障
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/problem/14666
// Memory Limit: 4 MB
// Time Limit: 14666000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
const int N = 5e4+10;
int a[N],l[N],r[N];
//因为要不断求两段的和 所以用前/后缀和优化
void solve()
{int yangli;scanf("%lld",&yangli);stack<int> st;//单调栈int cs=0;while(yangli--){cs++;memset(l,0,sizeof(l));memset(r,0,sizeof(r));int n;scanf("%lld",&n);for(int i=1;i<=n;i++) scanf("%lld",&a[i]);//正向遍历+单调递减栈 求左边第一个比他高的山st = stack<int> ();//清空栈for(int i=1;i<=n;i++){int num = 0;//用来计数（弹出栈的数量、比他小的数量、防御力）while(!st.empty() && a[st.top()] < a[i]){st.pop();num++;}if(!st.empty()) l[i] = l[i-1] + num + 1;//前面还有比他高的山，防御值为num+1else l[i] = l[i-1] + num;st.push(i);}st = stack<int> ();//逆向遍历+单调递减栈 求右边第一个比他高的山for(int i=n;i>=1;--i){int num=0;while(!st.empty() && a[st.top()] < a[i]){st.pop();num++;}if(!st.empty()) r[i] = r[i+1] + num + 1;else r[i] = r[i+1] + num;st.push(i);}int mx = -1,index = 0;for(int i=1;i<=n;i++){//至于为什么是l[n] - (l[i] + r[i+1])，因为l[n]/r[1]都表示防御总数 //要求减少多少，就需要用总数减去（去掉这座山时的总数）即这座山与之前的//所有总和+下一座山与其之后所有山的总和（也就是剔除了这座山和下一座山之//间的数量）if(l[n] - (l[i] + r[i+1]) > mx){mx = l[n] - (l[i] + r[i+1]);index = i;}}printf("Case #%lld: %lld %lld\n",cs,index+1,mx);}
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

吐泡泡 

这道题一开始一直用暴力模拟没去想栈，看来还是写的少，要多去做题体会这种思想增加熟练度

// Problem: 吐泡泡
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/problem/15029
// Memory Limit: 2 MB
// Time Limit: 15029000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se secondvoid solve()
{string s;cin>>s;stack<char> st;for(auto ch : s){if(st.empty()) st.push(ch);else{if(!st.empty() && ch==st.top()){st.pop();if(ch=='o'){if(!st.empty() && st.top()=='O') st.pop();else st.push('O');}else continue;}else st.push(ch);}}string ans;while(!st.empty()){ans += st.top();st.pop();}for(int i=ans.size()-1;i>=0;--i) cout<<ans[i];cout<<endl;
}signed main()
{IOSint T=1;cin>>T;while(T--) solve(); return 0;
} 

bitset：

常见函数用法：

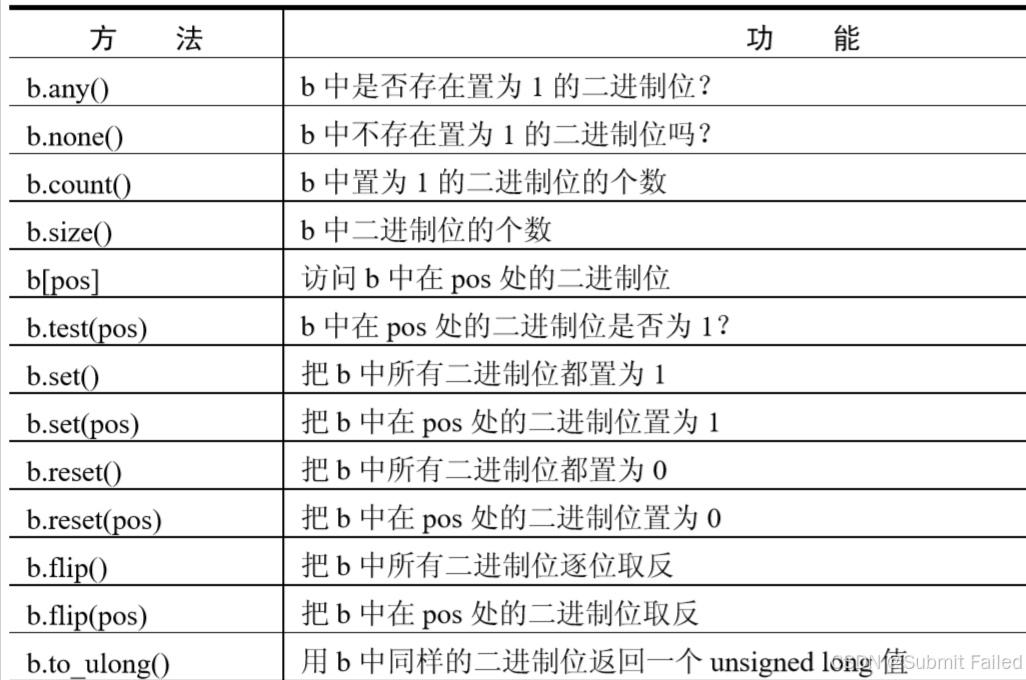
一般是先用bitset将元素转为二进制：

bitset<33> b(100);//长度为33，且将100转为二进制保存在二进制数组b中

需要注意的是：转化后的二进制数组与普通数组顺序相反，其首尾元素b[0] 在最后（最右边的元素），这样保证了后续能更方便的对其进行操作。

看一些例题：

小红组比赛

这种题其实可以用dp来写，但是像这种判断true和false的组合问题，还是建议用bitset转为二进制来模拟，转为二进制之后下标就表示数的具体的值，用0和1来判断这个数能否被组成，这时候因为每场比赛只能选一个题目，所以在遍历时要用上一场比赛作为基础来累加（左移即可），同一场比赛之间不能干扰，所以要在每场比赛遍历结束之后再更新，遍历过程中用一个中间变量通过或运算记录就好了。

// Problem: 小红组比赛
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/problem/276144
// Memory Limit: 2 MB
// Time Limit: 276144000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
const int N = 10010;
int n,m,tgt;void solve()
{cin>>n>>m;bitset<N> b,t;//bitset将转为二进制数组时，最右端是开头的b[0]；b.set(0);           //将0处转化为1 和为0是可行的for(int i=1;i<=n;i++){t.reset();//清零操作for(int j=1;j<=m;j++){int x;cin>>x;t |= (b<<x);//b<<x就相当于将b中的所有的数都+了一个x（往左移动了x位）//每次左移都是基于上一场比赛而不是这一场比赛，所以b要在最后更新，这里的b一直是之前的所有比赛为基础而不包括当前的比赛的前几个题目}b = t;//每场比赛只能选一个所以最后更新b}cin>>tgt;int ans;for(int i=tgt,j=tgt;j>0||i<=N;i++,j--){if(j==-1) j++;if(b[i]){ans = i-tgt;break;}if(b[j]){ans = tgt-j;break;}}cout<<ans<<endl;
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

如果可以重复选择的话就变为了：

b |= (b<<x);//每次选择都要累加

还有一个相似的题目：

简单瞎搞题

因为也是只能从区间里面选择一个，所以也是在每次添加进来一个区间都要用上一次的结果去遍历区间最后再更新，要求最后有多少种的话就只需要输出二进制中1的个数即可。

// Problem: 简单瞎搞题
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/problem/17193
// Memory Limit: 2 MB
// Time Limit: 17193000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
const int N = 1e6+10;
bitset<N> b,t;void solve()
{int n;cin>>n;b.set(0);//初始化while(n--){t.reset();//清空tint l,r;cin>>l>>r;for(int i=l;i<=r;i++) t |= (b<<(i*i));//每一次都是基于上一个n的bb = t;//最后更新b}	cout<<b.count();
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

起床困难综合征

用了long long之后常数与其运算的时候应该用 x(常数)LL !!!否则就会爆int

这样用暴力枚举的话肯定会超时，所以我们可以设一个全为0的二进制数和一个全为1的二进制数，这样就可以包含所有数据范围内的二进制数（因为每一位只能取0或1），如果进行位运算之后当前位置变成了1就需要考虑了（因为0乘任何数都为0，现在得到的是最后的每一位的二进制情况，还需要把二进制转为十进制），但是现在的二进制可能并不是答案，因为他可能比答案要大，所以就要对每一位进行判断，(因为要使答案最大，所以尽量在高位取1【比如011111也小于100000】)。

如果这位原本就是0后来变为1了那就可以直接取不要白不要（不会对累加更不会超出m的范围） 

#include <bits/stdc++.h>
using namespace std;
#define int long long 
//常数一定要加LL！！！
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
bitset<35> p0,p1;
int n,m;void solve()
{cin>>n>>m;p0.reset();//每一位都是0，最小值 p0[i]为1说明这一位本来是0最后变成了1p1.set();//每一位都是1，最大值   p1[i]为1说明这一位本来是1最后变成了1//因为每一位只可能是0或1 所以用两个bitset枚举每一位，找出每一位最后能变成的情况while(n--){string s;int t;cin>>s>>t;if(s=="AND") p0&=t,p1&=t;else if(s=="OR") p0|=t,p1|=t;else p0^=t,p1^=t;}//只需要看哪一位最后变成了1int ans=0,x=0;for(int i=30;i>=0;i--)//从30开始不能超出30，因为根本取不到更大的数{//优先判断p0，表示这一位上原本是0，操作之后变为了1，原本是0对x没有累加效果，想让ans最大，肯定要选if(p0[i]) ans+=(1<<i);//否则的话要尽量ans大即尽量高位是1 但是又不能超出范围限制else if(p1[i] && x+(1LL<<i) <= m) ans+=(1LL<<i),x+=(1LL<<i); }cout<<ans<<endl;
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

拓扑排序：

拓扑排序（Topological Sorting）是图论中的一种重要算法，主要用于处理有向无环图（DAG, Directed Acyclic Graph）的节点排序问题。它的核心思想是：对于图中的每个有向边 (u, v)，节点 u 在排序结果中必须出现在节点 v 之前。

拓扑排序的核心价值在于解决 “依赖关系下的顺序规划” 问题。它不仅能生成可行的执行顺序，还能检测系统中是否存在循环依赖，是解决许多实际问题的基础算法。

拓扑序列可以判断有向图中是否有环，可以生成拓扑序列。

Kahn（卡恩）算法
每个点通过有向边都有几个邻点，e[x]存点x的邻点（当然也可以用map构成映射关系），用tp存拓扑序列，再开一个数组，是x的入度数组din[x]存点x的入度。
算法的核心用队列维护一个入度为0的节点的集合

1.初始化，队列q压入所有入度为0的点。
2.每次从q中取出一个点x放入数组tp。
3.然后将x的所有出边删除。若将边（x,y)删除后，y的入度变为0，则将y压入q中。
4.不断重复2.3过程，直到队列q为空。
5.若tp中的元素个数等于n，则有拓扑序，否则，有环。

先来看一道题目：

视频讲解来源于：拓扑排序

软件构建

这是一道拓扑排序的经典例题，可以保存下来多看看。

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
int n,m;void solve()
{cin>>n>>m;vector<int> indegree(n);//用于存放每个节点的入度 入度用于判断当前节点是否能基于这个点作为起点开始往下找（入队）unordered_map<int,vector<int>> mp;//用于存放每个节点连着哪些点（哪些节点依赖于这个）while(m--){int k,v;//v节点依赖于k节点（k节点作为v的一个入度）cin>>k>>v;indegree[v]++;//入度加一mp[k].push_back(v);//k节点连着v}queue<int> que;//用队列实现卡恩算法（类似于BFS）  队列中存放的都是入度为0的点用于之后的往下搜索vector<int> topo;//用于存放最终的线性关系for(int i=0;i<n;i++)if(indegree[i]==0) que.push(i);//一开始就将所有入度为0的点存入队列，保证一批一批起点的入队while(!que.empty()){int current = que.front();que.pop();topo.push_back(current);//将每个起点依次存入最终数组中vector<int> note = mp[current];//因为要将这个点删除 所以这时应该把当前节点所有连着的点的入度都--（即删除这条两个节点之间的边，删除这两个节点之间的联系）for(int i=0;i<note.size();i++){indegree[note[i]]--;if(indegree[note[i]]==0) que.push(note[i]);//如果当前的节点入度为0说明已经可以作为起点了}}if(topo.size() == n)//说明没有形成环的 都可以按照顺序输出{for(int i=0;i<n-1;i++) cout<<topo[i]<<' ';cout<<topo[n-1]<<endl;}else cout<<-1<<endl;
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

现在有了拓扑排序的思想，就可以结合bitset来解决下一道题目了：

可达性统计

首先要统计每一个点能够到达的所有点，暴力肯定很乱，首先要进行排序，确保有线性关系才能知道谁基于谁（谁依赖谁），这样就是拓扑排序，然后就可以对排序之后的图逆序遍历不断累加可以到达的点！！！此时统计就可以用bitset来实现，对每一个点都开一个bitset，大小为所有可能到达的点，如果可到达就标记为1（true）而累计只需要或运算即可完成【用空间换时间！】最终每个点的可达点就是该点的bitset的.count（1的个数）~

// Problem: 可达性统计
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/166/
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define PII pair<int,int>
#define fi first
#define se second
const int N = 3e5+10;
int n,m;
vector<int> topo,indegree(N);
unordered_map<int,vector<int>> mp;
bitset<30010> dp[N];void tuopu()//拓扑排序
{queue<int> q;for(int i=1;i<=n;i++)if(!indegree[i]) q.push(i);while(!q.empty()){int cur=q.front();q.pop();topo.push_back(cur);vector<int> note = mp[cur];for(int i=0;i<note.size();i++){indegree[note[i]]--;if(!indegree[note[i]]) q.push(note[i]);}}
}void solve()
{cin>>n>>m;while(m--)//建图{int x,y;cin>>x>>y;indegree[y]++;mp[x].push_back(y);}tuopu();//拓扑排序之后要倒着来 逆序可以确保处理一个节点时它的后继节点已经被计算过了for(int i=n-1;i>=0;--i){int t = topo[i];dp[t][t]=1;//自己可达自己所以给自己变为truefor(auto it : mp[t]) dp[t] |= dp[it];//统计可以到达的所有的点}for(int i=1;i<=n;i++) cout<<dp[i].count()<<endl;
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
} 

 逆序可以确保处理一个节点时它的后继节点已经被计算过了

如果害怕用map的log级别的查询超时，可以换用另一位大神的数组O(1)查询方式：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=3e5+5;
int n,m,a,b;
vector <int>e[N],tp;//e[N]存x的邻点，tp存拓扑序列 
int din[N];//存x的入度，当x的入度为0时就可以添加到拓扑序中了 
bitset<30005>dp[N]; 
bool toposort()
{queue<int>q;for(int i=1;i<=n;i++)if(din[i]==0)q.push(i);//将一开始入度为0的点压入队列 while(q.size())//当q不空的时候 {//因为q中都是入度为0的点，且是有序的 int x=q.front(); //取队首元素 q.pop();//记得要弹出 tp.push_back(x);//存入tp数组中 for(auto c:e[x])//少了一个点，那么从这个点出来的边都要删除 {if(--din[c]==0)//如果删除后，入度等于0 q.push(c);//就压入队列 }}
}
signed main()
{cin>>n>>m;//n个点m条边 for(int i=0;i<m;i++){cin>>a>>b;//(a,b) e[a].push_back(b);//存边 din[b]++;//记录入度的个数 }toposort();//拓扑排序 for(int i=n-1;i>=0;i--){int t=tp[i];dp[t][t]=1;//每个节点可达自身，所以赋值为1 for(auto c:e[t])//将所有后继节点的可达集合进行“或”操作 dp[t]|=dp[c];//c是t的后继 }for(int i=1;i<=n;i++)cout<<dp[i].count()<<endl;//每个节点的bitset值中的1的个数就是可达的数量 return 0;
}

可恶的拓扑算法，今天终于要对你施展手脚了！