算法训练营day23 39. 组合总和、 40.组合总和II 、131.分割回文串
回溯算法的第二篇博客!第一遍刷题有点吃力,还是优先掌握思维逻辑,后面随着代码量的提升,慢慢打磨代码思维
注:本篇博客图片引用自《代码随想录》
39. 组合总和(可重复选取)
同一个数字可以无限制重复被选取,这个条件,看起来就很难,看了答案的过程之后,发现这个算法在横向部分是有“压缩”的成分在的,大家可以感受下,感觉又加深了一些对于这个算法的理解
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
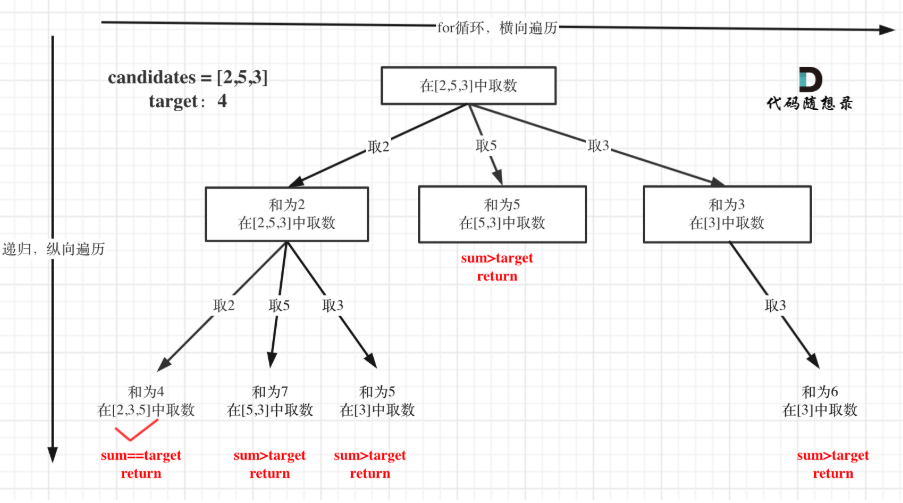
回溯过程
- 递归函数参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
首先是题目中给出的参数,集合candidates, 和目标值target。此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
本题还需要startIndex来控制for循环的起始位置
- 递归终止条件
只要选取的元素总和超过target,就返回
- 单层搜索的逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。重复选取的部分需要注意
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:result = []self.backtracking(candidates, target, 0, 0, [], result)return resultdef backtracking(self, candidates, target, total, startIndex, path, result):if total > target:returnif total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):total += candidates[i]path.append(candidates[i])self.backtracking(candidates, target, total, i, path, result)# 注意i参数, 因为可重复选取total -= candidates[i]path.pop()剪枝优化
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
在求和问题中,排序之后加剪枝是常见的套路!
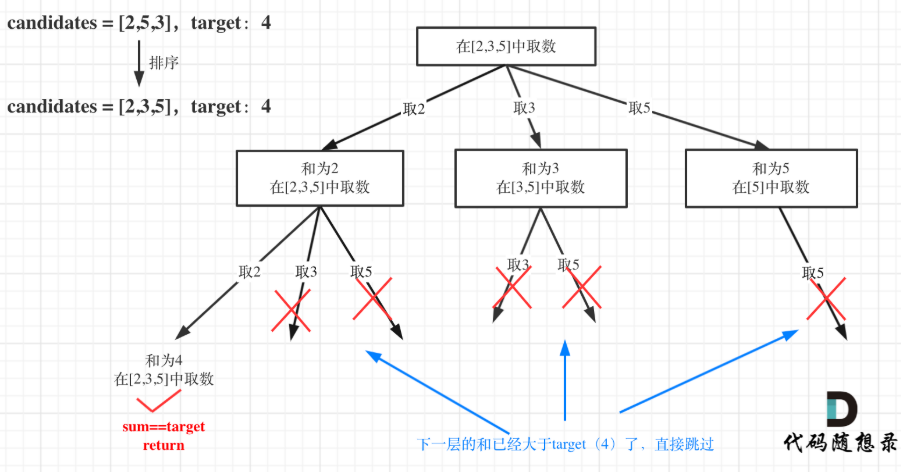
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:result = []candidates.sort() # 需要排序!重点理解为什么需要排序self.backtracking(candidates, target, 0, 0, [], result)return resultdef backtracking(self, candidates, target, total, startIndex, path, result):# if total > target:# returnif total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if total + candidates[i] > target:break # 重点理解为什么是break, 不是continue!total += candidates[i]path.append(candidates[i])self.backtracking(candidates, target, total, i, path, result)# 注意i参数, 因为可重复选取total -= candidates[i]path.pop()40.组合总和II(不重复)
这个题目要求不能重复选取其实不是最大的问题,最大的问题是候选者数组中存在重复元素!如果大家了解了我之前题目中解题的代码,会发现存在重复元素是一个很大的问题——元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。因为这样的话,之前的横向“压缩”的过程会遇到困扰
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。如下图所示:这个地方其实不复杂,只要深入理解了我们之前的组合逻辑,就好理解了
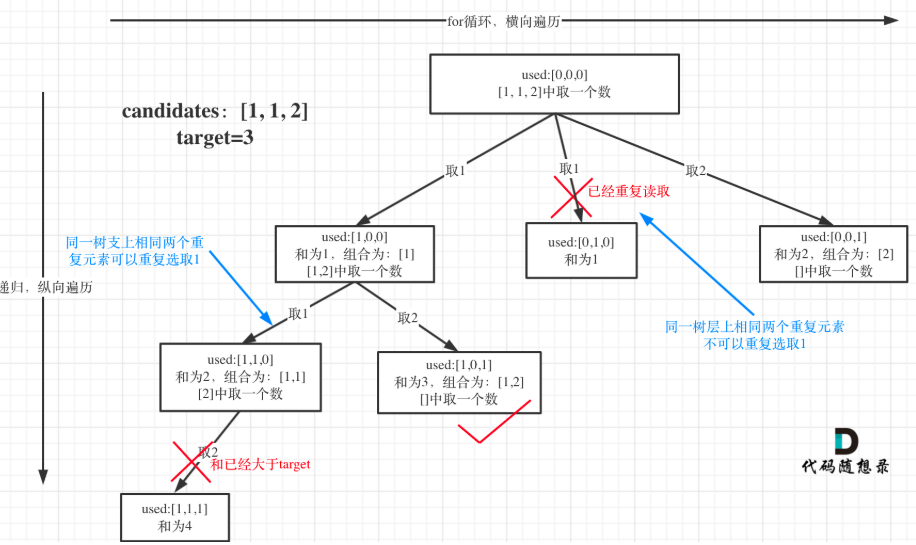
回溯过程
- 递归函数参数
与上一题套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
- 递归终止条件
终止条件为 sum > target 和 sum == target。
- 单层搜索的逻辑
前面我们提到:要去重的是“同一树层上的使用过”,如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。此时for循环里就应该做continue的操作。
代码实现
这个代码实现没有使用used数组,只判断了树层之间的不同会跳过,没有判断树枝的过程,used数组包含了树枝判断的过程,但是题目中没有要求,所以这个版本代码实现过程中没有使用used数组
class Solution:def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:result = []# 需要排序 方便去重candidates.sort()self.backtracking(candidates, target, 0, 0, [], result)return resultdef backtracking(self, candidates, target, total, startIndex, path, result):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if i > startIndex and candidates[i] == candidates[i - 1]:continue# 不可以出现相同的组合, 因为前面已经包含了, 所以遇到重复的需要删掉if total + candidates[i] > target:breaktotal += candidates[i]path.append(candidates[i])# 这个地方是不可以重复选取, 所以要 i+1 来压缩候选者数组self.backtracking(candidates, target, total, i + 1, path, result)total -= candidates[i]path.pop()
增加对于树层和树枝的理解
图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
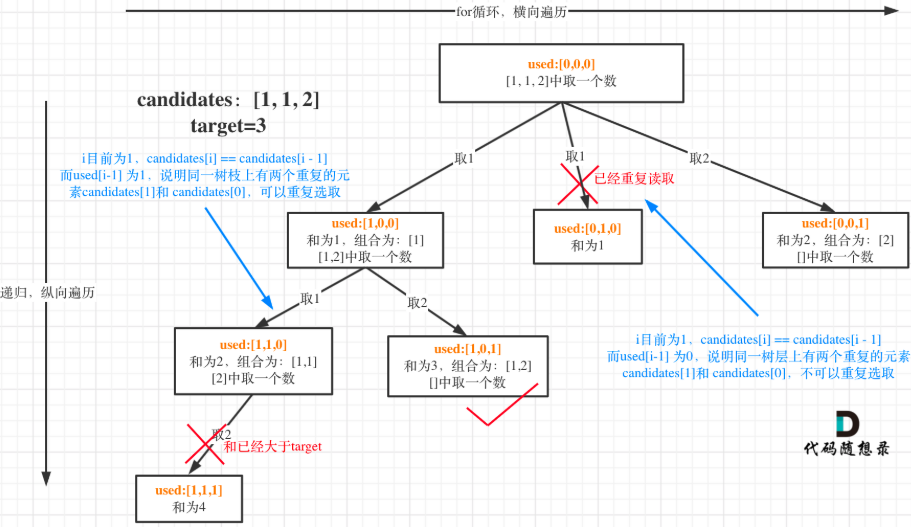
class Solution:def backtracking(self, candidates, target, total, startIndex, used, path, result):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):# 对于相同的数字,只选择第一个未被使用的数字,跳过其他相同数字if i > startIndex and candidates[i] == candidates[i - 1] and not used[i - 1]:continueif total + candidates[i] > target:breaktotal += candidates[i]path.append(candidates[i])used[i] = Trueself.backtracking(candidates, target, total, i + 1, used, path, result)used[i] = Falsetotal -= candidates[i]path.pop()def combinationSum2(self, candidates, target):used = [False] * len(candidates)result = []candidates.sort()self.backtracking(candidates, target, 0, 0, used, [], result)return result
131.分割回文串
本题这涉及到两个关键问题:
- 切割问题,有不同的切割方式(找到组合方式、模拟切割过程)
- 判断回文
大家理解这个图,可以看出切割和组合有相似之处,组合是以个为单位,切割相对复杂一点——只是截取的部分以递增方式处理1 12 123->1.2 1.23 12.3 123 ->1.2.3 ……
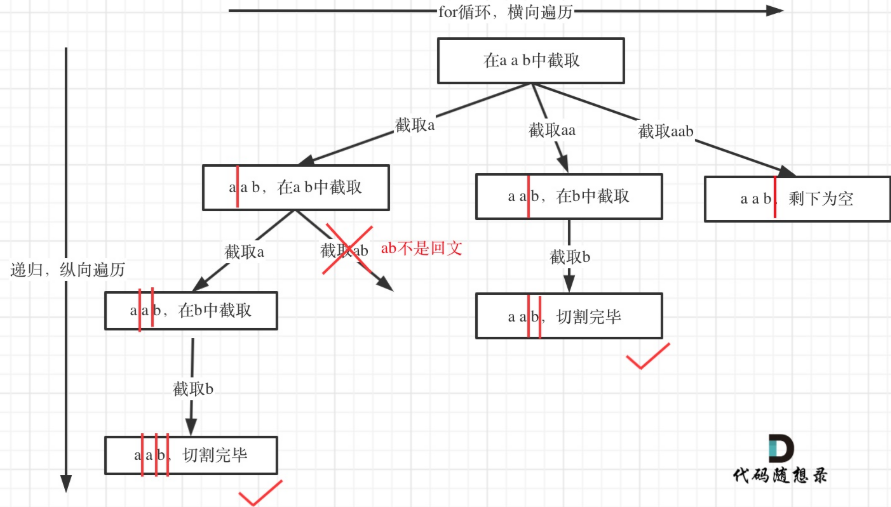
回溯过程
- 递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
- 递归函数终止条件
从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
在代码里什么是切割线呢——在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
- 单层搜索的逻辑
递归循环中如何截取子串呢——在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
判断回文子串
最后我们看一下回文子串要如何判断了,判断一个字符串是否是回文。可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
class Solution:def partition(self, s: str) -> List[List[str]]:'''递归用于纵向遍历for循环用于横向遍历当切割线迭代至字符串末尾,说明找到一种方法类似组合问题,为了不重复切割同一位置需要start_index来做标记下一轮递归的起始位置(切割线)'''result = []self.backtracking(s, 0, [], result)return resultdef backtracking(self, s, start_index, path, result ):if start_index == len(s):result.append(path[:]) # 切割完成, 收割结果returnfor i in range(start_index, len(s)):# 判断是否为回文字符串if self.is_palindrome(s, start_index, i): # 这里是对于s的位置判定——左闭右闭# or 使用切片正序vs倒序是否一致判断# if s[start_index: i + 1] == s[start_index: i + 1][::-1]:# or 使用all函数# all(s[i] == s[len(s) - 1 - i] for i in range(len(s) // 2))path.append(s[start_index:i + 1]) # 这里是切片判定——左闭右开self.backtracking(s, i + 1, path, result)path.pop()def is_palindrome(self, s: str, start: int, end: int) -> bool:i = start# i: int = startj = end# j: int = endwhile i < j:if s[i] != s[j]:return Falsei += 1j -= 1return True
优化判定回文函数
这里可以提前了解一下动态规划的概念,例如给定字符串"abcde", 在已知"bcd"不是回文字串时, 不再需要去双指针操作"abcde"而可以直接判定它一定不是回文字串。具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。
大家如果熟悉动态规划这种算法的话, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤。
动态规划的具体依赖关系
判断子串s[i:j+1]是否为回文串时,有以下几种情况:
- 当子串长度为 1(也就是
i == j)时,肯定是回文串。 - 当子串长度为 2(即
j - i == 1)时,只有s[i]和s[j]相等,该子串才是回文串。 - 当子串长度大于 2 时,需要满足
s[i] == s[j],并且去掉首尾字符后的子串s[i+1:j]也得是回文串。
从第三种情况能看出,isPalindrome[i][j]的值依赖于isPalindrome[i+1][j-1]。如果采用正序遍历i,在计算isPalindrome[i][j]时,isPalindrome[i+1][j-1]可能还没有被计算出来,这就会导致错误的结果。
class Solution:def partition(self, s: str) -> List[List[str]]:result = []isPalindrome = [ [False] * len(s) for _ in range(len(s)) ]# 二维数组self.computerPalindrome(s, isPalindrome)self.backtracking(s, 0, [], result, isPalindrome)return resultdef backtracking(self, s, startIndex, path, result, isPalindrome):if startIndex >= len(s):result.append(path[:])return # 切割完整个字符串直接退出for i in range(startIndex, len(s)):if isPalindrome[startIndex][i]: # 判断区间是否是回文字符串substring = s[startIndex:i + 1]path.append(substring)self.backtracking(s, i + 1, path, result, isPalindrome)path.pop()def computerPalindrome(self, s, isPalindrome):for i in range(len(s) - 1, -1, -1):# 生成一个倒序的整数序列# 注意数组索引和range区间即可for j in range(i, len(s)):# 对从索引i开始到字符串末尾的所有子串进行遍历if j == i:isPalindrome[i][j] = Trueelif j - i == 1:isPalindrome[i][j] = (s[i] == s[j])else:isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i + 1][j - 1])
