当前位置：首页 > news >正文

2022年CIE SCI2区TOP，NSGA-II+直升机-无人机搜救任务分配，深度解析+性能实测

news 2025/7/17 6:31:11

1.摘要

无人机任务分配对于保障搜救活动高效有序开展具有重要意义，但现有研究较少考虑无人机作业环境与性能对任务分配的影响。针对低空风场和地形因素对无人机能耗与性能的影响，本研究提出了直升机释放位置选择与任务分配模型。考虑到地形因素会影响无人机探测区域，采用主成分分析法确定各搜救点的搜救等级，并运用聚类分析确定无人机悬停续航能力。结合无人机性能、低空风场等影响电池能耗的因素，构建无人机释放位置选择模型，采用改进二进制蝙蝠算法求解。根据释放位置规划结果，建立以总搜救成本最小、无人机数量最少及多机任务均衡为目标的优化模型，运用NSGA-II进行求解。

直升机-无人机搜救场景

2.数学模型

参数定义

无人机释放位置选择模型

无人机任务分配必须将实际避障能耗纳入考量，本研究基于最坏工况假设，建立以下能量管理机制：满载无人机必须保持2/3能量状态抵达目标点，并预留1/3能量用于返航。

$minZ=∑j∈M∑k∈NczjkSjk+∑j∈MFjxjminZ=\sum_{j\in M}\sum_{k\in N}cz_{jk}S_{jk}+\sum_{j\in M}F_jx_j$

无人机搜救任务分配模型

目标函数主要包括三部分，即无人机的搜救成本，以及使用的无人机数量和完成任务所需的总时间。应考虑无人机的任务平衡性和合理性。目标函数要求总成本最小，包括无人机飞行和悬停产生的航程成本，前者与无人机飞行航程能耗成正比，后者与悬停时间成正比。

$minZ1=minc(∑k∈K∑i∈P∑j∈Psijyijxijk+∑i∈Nsi)minZ_1=minc\left(\sum_{k\in K}\sum_{i\in P}\sum_{j\in P}s_{ij}y_{ij}x_{ijk}+\sum_{i\in N}s_i\right)$

无人机的实际数量在实践中是有限的，因此使用的无人机数量应尽可能低。
$minZ2=min∑k∈K∑j∈Px0jkminZ_2=min\sum_{k\in K}\sum_{j\in P}x_{0jk}$

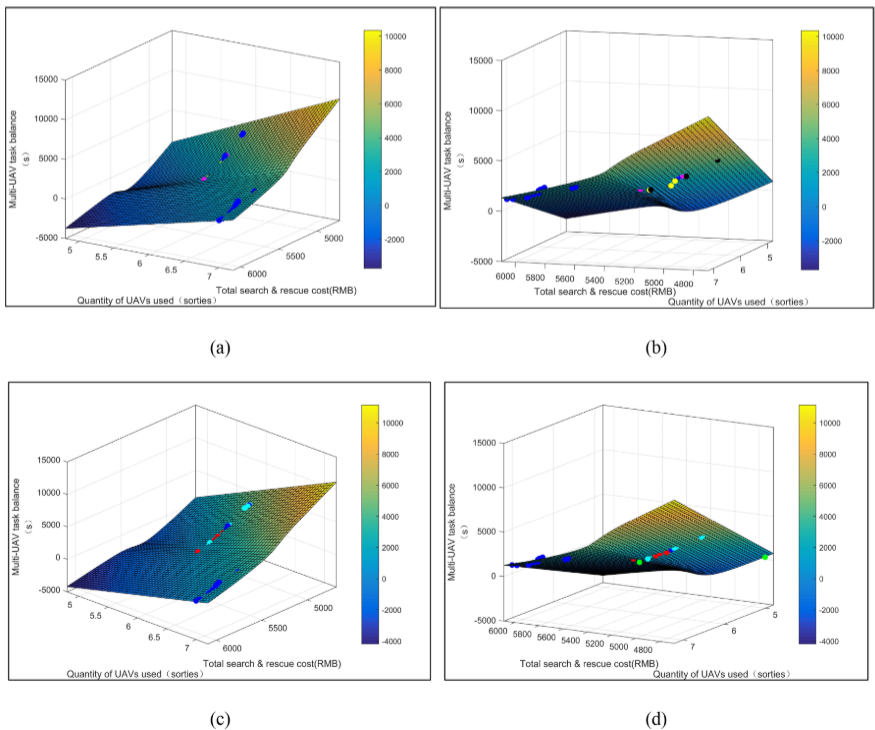
考虑任务平衡性，在考虑成本问题的同时，将不同无人机花费任务的时间最大差异减小到最小。
$minZ3=min{Tkmax−Tkmin},Tkmax,Tkmin∈TminZ_3=min\{T_{kmax}-T_{kmin}\},T_{kmax},T_{kmin}\in T$

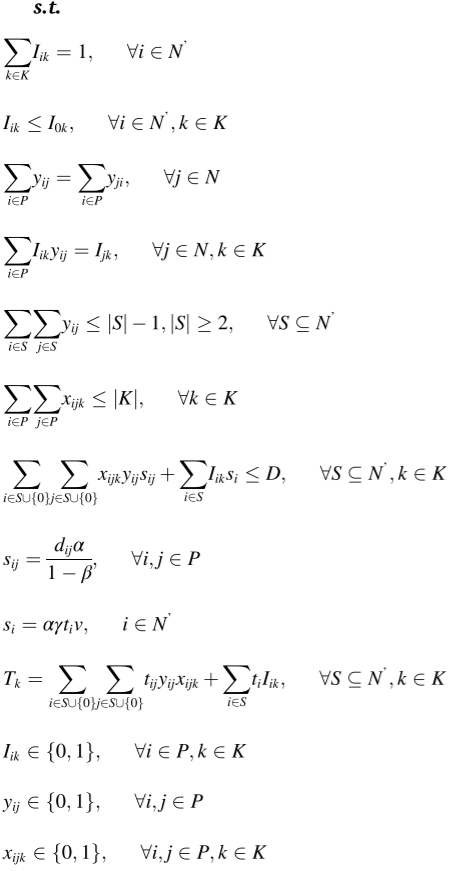
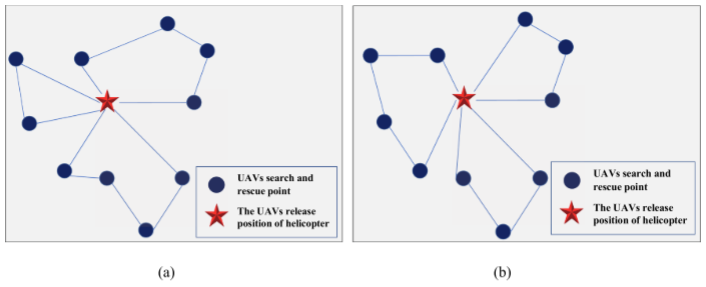
无人机任务分配结果；(a)只考虑成本目标时的分配结果；(b)同时考虑成本和任务平衡时的分配结果

3.求解方法

主成分分析法对搜救点进行分级

无人机探测盲区算法

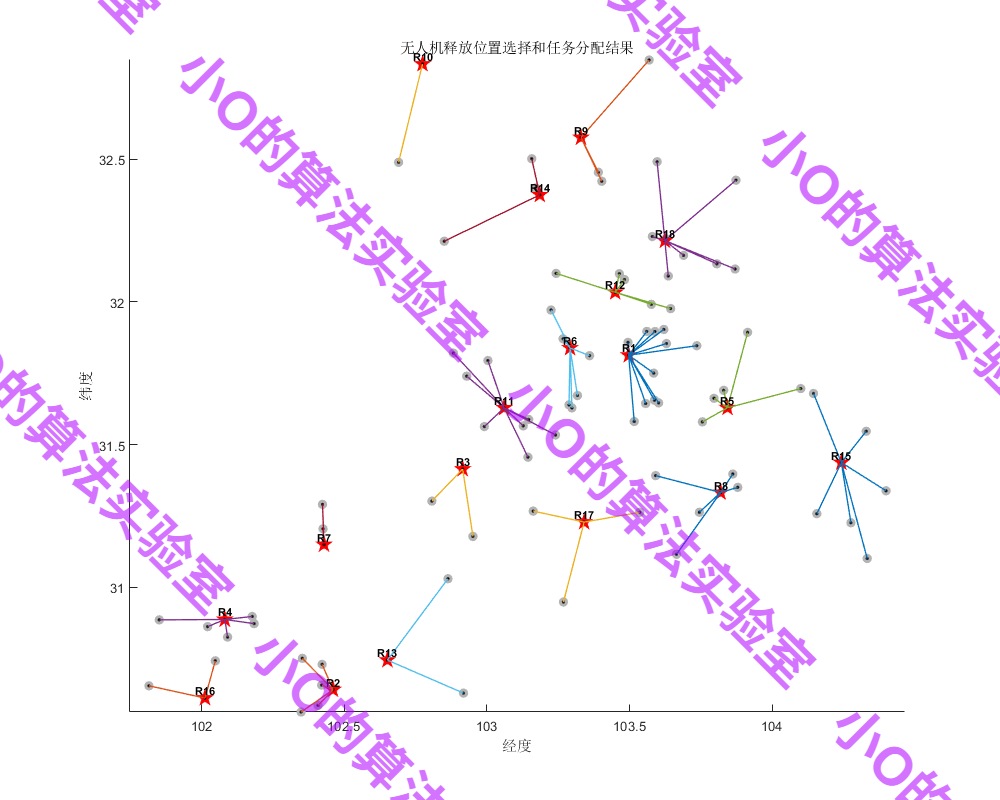
IBBA解决无人机从直升机上的释放位置

基于NSGA-II的无人机任务分配

考虑到多无人机任务分配问题的局限性，参考文献（Wang et al., 2018），采用双染色体编码方法进行编码，其中染色体I表示目标序列，染色体II表示目标序列在I上的切割位置。I上的每个基因表示每个搜索目标的索引，基因总数为NT。任意一个基因的值不得小于其前一个基因的值，基因号为（NU−1）。

NSGA-II采用快速非支配排序，拥挤度比较算子，个体 $i$ 的拥挤距离：
$L(i)=∑k=13Zk×(L(i+1)−L(i−1))/(Zkmax−Zkmin)L(i)=\sum_{k=1}^3Z_k\times(L(i+1)-L(i-1))/\left(Z_k^{max}-Z_k^{min}\right)$

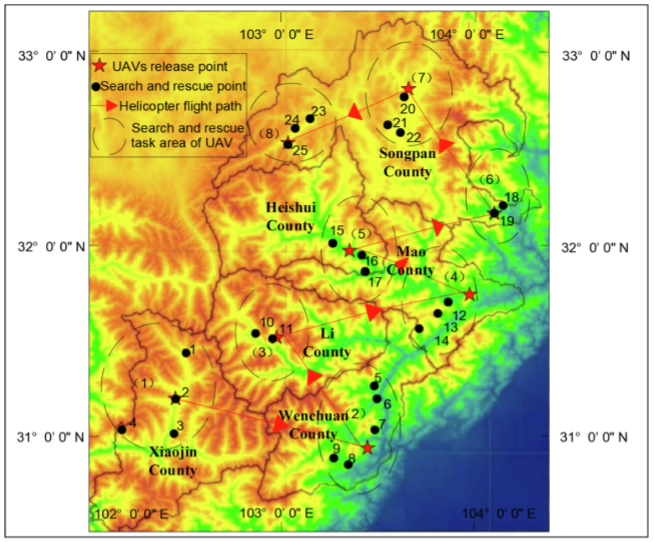
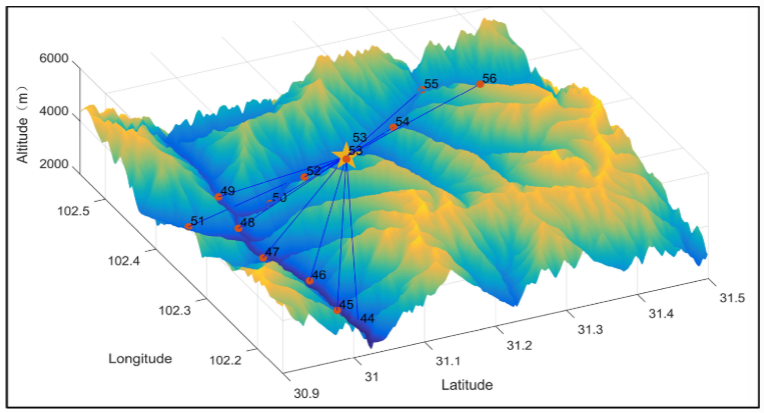
4.结果展示

论文仿真

5.参考文献

[1] Zhang M, Li W, Wang M, et al. Helicopter–UAVs search and rescue task allocation considering UAVs operating environment and performance[J]. Computers & Industrial Engineering, 2022, 167: 107994.