当前位置：首页 > news >正文

深度学习中的激活函数：从原理到 PyTorch 实战

news 2025/7/16 9:11:16

一、为什么需要激活函数？

二、常用激活函数详解

2.1 Sigmoid 函数

2.2 Tanh 函数

2.3 ReLU 函数

2.4 Leaky ReLU

2.5 Softmax 函数

三、激活函数如何选择？

四、激活函数的实际应用

五、总结

激活函数是神经网络的 "灵魂"，它为模型注入了非线性能力，让神经网络能够拟合复杂的现实世界数据。本文将结合理论和代码实例，深入浅出地讲解常用激活函数的原理、特点和 PyTorch 实现方法。

一、为什么需要激活函数？

想象一下，如果没有激活函数，无论神经网络有多少层，都只是在做线性变换。就像用多个一次函数叠加，结果仍然是一次函数，无法拟合曲线关系。

激活函数的作用就是引入非线性变换，让神经网络能够处理图像识别、自然语言处理等复杂任务。没有激活函数，深度学习就无从谈起。

二、常用激活函数详解

2.1 Sigmoid 函数

Sigmoid 是早期神经网络中常用的激活函数，数学公式为：

它能将任意输入映射到 (0,1) 区间，非常适合作为二分类问题的输出层。

特点：

输出范围 (0,1)，可表示概率
导数计算方便：σ'(x) = σ(x)・(1-σ(x))
缺点是容易出现梯度消失

PyTorch 实现：

import torch
import torch.nn.functional as Fx = torch.tensor([-1.0, 0.0, 1.0, 2.0])
y = torch.sigmoid(x)  # 或 F.sigmoid(x)
print(y)  # 输出: tensor([0.2689, 0.5000, 0.7311, 0.8808])

2.2 Tanh 函数

Tanh (双曲正切) 函数解决了 Sigmoid 输出不是零中心的问题，公式为：

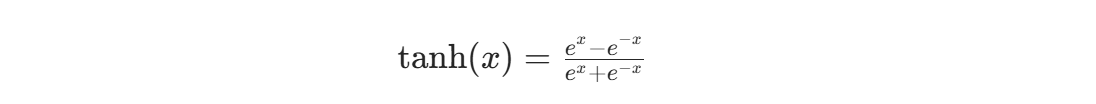
特点：

输出范围 (-1,1)，零中心分布
收敛速度比 Sigmoid 快
仍然存在梯度消失问题

PyTorch 实现：

x = torch.tensor([-1.0, 0.0, 1.0, 2.0])
y = torch.tanh(x)
print(y)  # 输出: tensor([-0.7616, 0.0000, 0.7616, 0.9640])

2.3 ReLU 函数

ReLU 是目前最流行的激活函数，公式极其简单：

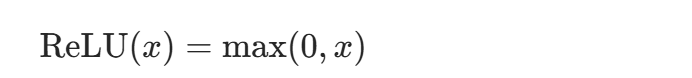
特点：

计算速度快，只需要比较操作
缓解梯度消失问题
可能出现 "神经元死亡" 现象（负数输入永远为 0）

PyTorch 实现：

x = torch.tensor([-1.0, 0.0, 1.0, 2.0])
y = torch.relu(x)  # 或 F.relu(x)
print(y)  # 输出: tensor([0.0000, 0.0000, 1.0000, 2.0000])

2.4 Leaky ReLU

为解决 ReLU 的神经元死亡问题，Leaky ReLU 在负数区域引入小斜率：

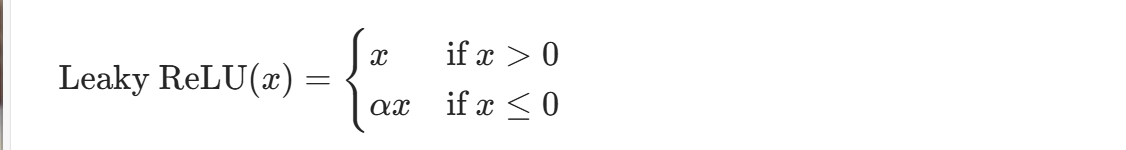
特点：

允许小的负梯度，避免神经元死亡
需要调整 α 超参数（通常 0.01）

PyTorch 实现：

x = torch.tensor([-1.0, 0.0, 1.0, 2.0])
leaky_relu = nn.LeakyReLU(negative_slope=0.01)
y = leaky_relu(x)
print(y)  # 输出: tensor([-0.0100, 0.0000, 1.0000, 2.0000])

2.5 Softmax 函数

Softmax 常用于多分类问题的输出层，能将输出转换为概率分布：

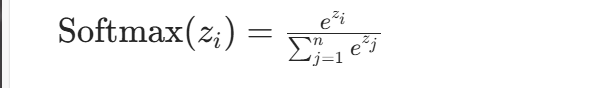
特点：

输出值之和为 1，可表示类别概率
放大类别间差异，突出最大概率类别
数值稳定性处理（内部自动减去最大值）

PyTorch 实现：

import torch
from torch import nn# 关闭科学计数法，方便查看
torch.set_printoptions(sci_mode=False)# 测试样例：2个样本，每个样本4个类别得分
x = torch.tensor([[-1, 2, -3, 4], [5, -6, 7, 10]], dtype=torch.float32)
sm = nn.Softmax(dim=1)  # dim=1表示按行计算y = sm(x)
print("Softmax输出:\n", y)
print("每行求和验证:", y.sum(dim=1))  # 应该都为1.0
print("预测类别:", y.argmax(dim=1))  # 输出概率最大的类别索引

输出结果：

Softmax输出:tensor([[ 0.0059,  0.1184,  0.0008,  0.8749],[ 0.0067,  0.0000,  0.0472,  0.9461]])
每行求和验证: tensor([1.0000, 1.0000])
预测类别: tensor([3, 3])

三、激活函数如何选择？

实际应用中不需要死记硬背，记住这个简单原则即可：

隐藏层：
- 优先使用 ReLU，计算快且效果好
- 如果 ReLU 出现神经元死亡，尝试 Leaky ReLU
- 避免使用 Sigmoid，可用 Tanh 替代
输出层：
- 二分类问题：Sigmoid（输出单个概率）
- 多分类问题：Softmax（输出概率分布）
- 回归问题：通常不需要激活函数

四、激活函数的实际应用

在 PyTorch 构建神经网络时，激活函数的使用非常灵活：

import torch
from torch import nn# 定义一个简单的全连接网络
class MyModel(nn.Module):def __init__(self, input_size, num_classes):super(MyModel, self).__init__()self.fc1 = nn.Linear(input_size, 64)self.fc2 = nn.Linear(64, 32)self.fc3 = nn.Linear(32, num_classes)def forward(self, x):x = torch.relu(self.fc1(x))  # 隐藏层用ReLUx = torch.relu(self.fc2(x))  # 隐藏层用ReLUif num_classes == 1:x = torch.sigmoid(self.fc3(x))  # 二分类用Sigmoidelse:x = torch.softmax(self.fc3(x), dim=1)  # 多分类用Softmaxreturn x# 二分类模型
binary_model = MyModel(input_size=10, num_classes=1)
# 多分类模型
multi_model = MyModel(input_size=10, num_classes=5)