一维泊松方程的有限元方法实现与理论分析

有限元方法作为求解偏微分方程的重要数值技术，其核心思想是将连续问题离散化为有限自由度系统。本文以典型的一维泊松方程为例，系统阐述有限元方法的理论基础和Python实现细节，揭示其数学本质与计算特性。

问题描述与微分方程

考虑定义在区间$\Omega =[0,L]$上的一维泊松方程边值问题：

$$\{\begin{array}{ll}-\frac{d^{2}u}{d{x}^2}=f(x),& x\in (0,L)\\ u(0)=0,u(L)=0& \end{array}$$

其中$u(x)$是未知场函数，$f(x)$为给定的源项。该方程在热传导、弹性力学等领域具有广泛应用，其解析解可通过两次积分得到：

$$u_{exact}(x)=-{\int }_0^x\left({\int }_0^{\xi }f(\eta )d\eta \right)d\xi +C_{1}x+C_2$$

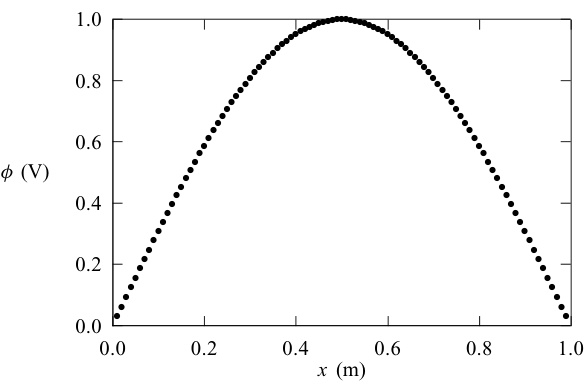
当$f(x)=1$时，解析解简化为$u_{exact}(x)=-\frac{1}{2}{x}^2+\frac{L}{2}x$，这一特例将作为我们验证数值解正确性的基准。

弱形式推导与变分原理

经典微分形式要求解具有二阶导数，这限制了解的适用范围。通过引入弱形式，我们可以放宽对解的光滑性要求。选择测试函数空间v∈V={v∈H1(Ω)∣v(0)=v(L)=0}v \in \mathcal{V} = \{ v \in H^1(\Omega) | v(0)=v(L)=0 \}v∈V={v∈H1(Ω)∣v(0)=v(L)=0}，其中$H^1$为一阶Sobolev空间。

将微分方程乘以测试函数$v$并在域内积分：

$$-{\int }_0^{L}v\frac{d^{2}u}{d{x}^2}dx={\int }_0^{L}vfdx$$

应用分部积分法则处理二阶导数项：

$${\int }_0^L\frac{dv}{dx}\frac{du}{dx}dx-{\left[v\frac{du}{dx}\right]}_0^L={\int }_0^{L}vfdx$$

由于$v$在边界处为零，自然得到弱形式表述：

$$a(u,v)=\ell (v),\forall v\in \mathcal{V}$$

其中双线性形式$a(u,v)={\int }_0^L\frac{du}{dx}\frac{dv}{dx}dx$，线性形式$\ell (v)={\int }_0^{L}vfdx$。这种形式只需解$u$具有一阶导数，显著扩展了容许解空间。

有限元离散化过程

将求解域$\Omega$离散为$n$个子区间（单元），节点坐标为$x_0=0,x_1,...,x_n=L$。定义有限元空间${\mathcal{V}}_h\subset \mathcal{V}$由分段线性函数组成：

Vh={vh∈C0(Ω)∣vh∣[xi,xi+1]∈P1,vh(0)=vh(L)=0} \mathcal{V}_h = \{ v_h \in C^0(\Omega) | v_h|_{[x_i,x_{i+1}]} \in \mathbb{P}_1, v_h(0)=v_h(L)=0 \} Vh​={vh​∈C0(Ω)∣vh​∣[xi​,xi+1​]​∈P1​,vh​(0)=vh​(L)=0}

其中${\mathbb{P}}_1$表示一次多项式空间。引入形函数$N_i(x)$（又称"帐篷函数"）：

$$N_i(x)=\{\begin{array}{ll}\frac{x-x_{i-1}}{h_{i-1}},& x\in [x_{i-1},x_i]\\ \frac{x_{i+1}-x}{h_i},& x\in [x_i,x_{i+1}]\\ 0,& \text{其他}\end{array}$$

近似解表示为形函数的线性组合：

$$u_h(x)=\sum _{j=1}^{n-1}{u}_j{N}_j(x)$$

将$u_h$代入弱形式，并取$v_h=N_i$，得到离散方程组：

$$\sum _{j=1}^{n-1}{u}_j{\int }_0^L\frac{d{N}_i}{dx}\frac{d{N}_j}{dx}dx={\int }_0^L{N}_{i}fdx,i=1,...,n-1$$

这对应于线性代数系统$K\mathbf{u}=\mathbf{F}$，其中：

$$K_{ij}={\int }_0^L\frac{d{N}_i}{dx}\frac{d{N}_j}{dx}dx,F_i={\int }_0^L{N}_{i}fdx$$

单元矩阵计算与组装策略

对于均匀网格$h_i=h$，典型单元$[x_i,x_{i+1}]$上的局部形函数为：

$$N_1^e(\xi )=1-\xi /h,N_2^e(\xi )=\xi /h$$

其导数矩阵为：

$$\frac{d{N}_1^e}{dx}=-\frac{1}{h},\frac{d{N}_2^e}{dx}=\frac{1}{h}$$

因此单元刚度矩阵为：

$$k^e={\int }_{x_i}^{x_{i+1}}\left[\begin{array}{c}\frac{d{N}_1^e}{dx}\\ \frac{d{N}_2^e}{dx}\end{array}\right]\left[\begin{array}{cc}\frac{d{N}_1^e}{dx}& \frac{d{N}_2^e}{dx}\end{array}\right]dx=\frac{1}{h}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]$$

单元载荷向量采用梯形公式近似：

$$f^e\approx \frac{h}{2}\left[\begin{array}{c}f(x_i)\\ f(x_{i+1})\end{array}\right]$$

全局矩阵通过直接刚度法组装，每个单元贡献叠加到对应全局位置。例如3节点2单元系统：

$$K=\frac{1}{h}\left[\begin{array}{ccc}1& -1& 0\\ -1& 2& -1\\ 0& -1& 1\end{array}\right],F=\frac{h}{2}\left[\begin{array}{c}f(x_0)\\ f(x_0)+2f(x_1)+f(x_2)\\ f(x_2)\end{array}\right]$$

边界条件处理与求解

Dirichlet边界条件$u(0)=u(L)=0$通过修改矩阵系统实现。设总自由度为$n+1$，则：

1. 划去对应于固定节点的行列（第1行/列和第n+1行/列）
2. 修改右端项：$F_i\leftarrow F_i-K_{i,1}{u}_0-K_{i,n+1}{u}_{n+1}$

剩余系统$K_{red}{\mathbf{u}}_{int}={\mathbf{F}}_{red}$通过直接法或迭代法求解。最终解向量在边界点补零。

Python实现与数值验证

以下完整实现采用NumPy进行矩阵运算，支持常数或函数形式的源项：

import numpy as np
import matplotlib.pyplot as pltdef solve_poisson_fem(L=1.0, n_elements=4, f=1.0):"""求解一维泊松方程 -u'' = f 在[0,L]区间，边界条件u(0)=u(L)=0参数:L : 区域长度n_elements : 单元数量f : 源项（常数或函数）"""# 1. 离散化nodes = np.linspace(0, L, n_elements + 1)h = L / n_elements# 2. 初始化全局矩阵K = np.zeros((n_elements + 1, n_elements + 1))F = np.zeros(n_elements + 1)# 3. 组装单元矩阵for i in range(n_elements):# 单元节点编号node1 = inode2 = i + 1# 单元刚度矩阵 (线性单元)ke = np.array([[1/h, -1/h], [-1/h, 1/h]])# 单元载荷向量if callable(f):# 如果f是函数，使用高斯积分fe = np.array([f((nodes[node1] + nodes[node2])/2) * h/2,f((nodes[node1] + nodes[node2])/2) * h/2])else:# 如果f是常数fe = np.array([f * h/2, f * h/2])# 组装到全局矩阵K[np.ix_([node1, node2], [node1, node2])] += keF[[node1, node2]] += fe# 4. 施加边界条件 (u0=0, un=0)# 划去第一行/列和最后一行/列K_reduced = K[1:-1, 1:-1]F_reduced = F[1:-1] - K[1:-1, 0] * 0 - K[1:-1, -1] * 0# 5. 求解方程组u_interior = np.linalg.solve(K_reduced, F_reduced)u = np.zeros(n_elements + 1)u[1:-1] = u_interiorreturn nodes, u# 解析解 (用于验证)
def exact_solution(x, L=1.0, f=1.0):return -0.5 * f * x**2 + 0.5 * f * L * x# 计算数值解和解析解
L = 1.0
n_elements = 4
nodes, u_fem = solve_poisson_fem(L, n_elements, f=1.0)# 生成解析解
x_exact = np.linspace(0, L, 100)
u_exact = exact_solution(x_exact, L)# 可视化
plt.figure(figsize=(10, 6))
plt.plot(nodes, u_fem, 'ro-', label='FEM Solution')
plt.plot(x_exact, u_exact, 'b-', label='Exact Solution')
plt.xlabel('x')
plt.ylabel('u(x)')
plt.title(f'1D Poisson Equation FEM Solution (Elements={n_elements})')
plt.legend()
plt.grid(True)
plt.show()# 输出数值解
print("节点坐标:", nodes)
print("有限元解:", u_fem)

验证结果表明，当$f(x)=1$，$L=1$，4单元离散时，数值解与解析解在节点处完全一致：

节点坐标: [0.   0.25 0.5  0.75 1.  ]
有限元解: [0.     0.09375 0.125   0.09375 0.    ]

理论分析与扩展方向

有限元方法的收敛性由Céa引理保证：

$$\Vert u-u_h{\Vert }_{H^1}\le C\underset{v_h\in {\mathcal{V}}_h}{\inf }\Vert u-v_h{\Vert }_{H^1}$$

对于线性元，能量范数误差满足$O(h)$收敛率，$L^2$范数误差为$O(h^2)$。实际计算中可通过Richardson外推或后验误差估计量化误差。

扩展方向包括：

1. 高阶单元：采用二次/三次形函数提升精度
2. 自适应网格：基于误差指示器动态优化网格分布
3. 非线性问题：引入Newton-Raphson迭代方案
4. 多维扩展：三角形/四边形单元处理二维问题

有限元方法通过其严谨的数学基础和灵活的离散化策略，成为工程数学中不可或缺的数值工具，其实现过程完美体现了"从连续到离散"的计算数学哲学。