描述统计1
SciPy是什么
-
SciPy是一个开源的 Python算法库和数学工具包
-
Scipy 是基于Numpy的科学计算库,用于数学、科学、工程学等领域
vv通过实例讲解SciPy的使用方法,如果想更多地了解SciPy,可以访问SciPy的官网
SciPy官网地址:SciPy
statsmodels介绍

statsmodels是什么
- statsmodels是一个Python软件包,为SciPy提供了补充,以进行统计计算,包括描述性统计以及统计模型的估计和推断
- statsmodels是擅长进行核心统计的库。这个多功能库混合了许多 Python 库的功能
statsmodels的使用方式
statsmodels有很多使用方式,这里仅举一例:
statsmodels的DescrStatsW类不仅可以用于进行变量的统计描述,更是进一步进行各种比较的基础对象。
class statsmodels.stats.weightstats.DescrStatsW(data : 希望分析的一维数组或者二维数据框weights = None : 案例权重,总和应当等于样本量ddof = 0 : 用于计算第二统计量的校正自由度,罕用
)
Pandas是什么
Pandas主要用于数据分析,这是最常用的Python库之一。它提供了一些最有用的工具来对数据进行探索、清理和分析。使用Pandas,可以加载、准备、操作和分析各种结构化数据
Pandas的两种数据结构
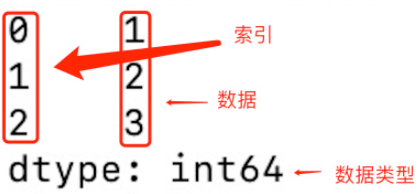
- Series
Series 类似表格中的一个列(column),也类似于一维数组,可以保存任何数据类型
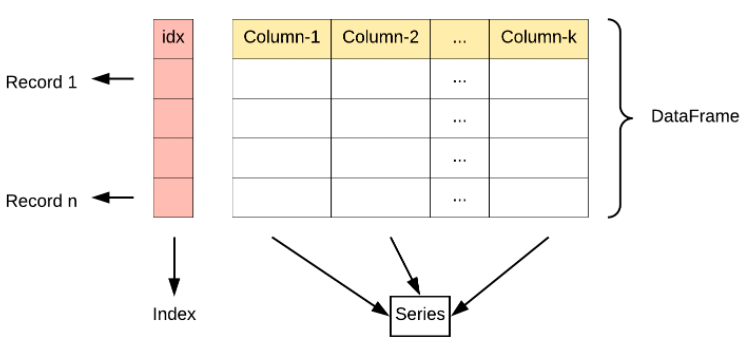
- DataFrame
DataFrame 是一个表格型的数据结构。DataFrame 既有行索引也有列索引,它可以被看做由 Series 组成的字典(共同用一个索引)
Anaconda介绍

Anaconda是一个包含了180多个科学包及其依赖项的Python发行版本
为什么要安装Anaconda
- 对于python初学者而言及其友好
Anaconda里添加了许多常用的功能包,如果单独安装python,这些功能包则需要一条一条自行安装
- Anaconda还附带捆绑了两个非常好用的交互式代码编辑器(Spyder、Jupyter notebook)
2. describe命令
df.describe( percentiles : 需要输出的百分位数,列表格式提供,如[.25, .5, .75]include = 'None' : 要求纳入分析的变量类型白名单 None (default) : 只纳入数值变量列 A list-like of dtypes : 列表格式提供希望纳入的类型 'all' : 全部纳入 exclude : 要求剔除出分析的变量类型黑名单,选项同上
)
ccss.describe() # 默认对数值类型进行描述统计
ccss.groupby('s0').s3.describe(percentiles=[.05,.1]) # 通过's0'列分组,然后对s3列求描述统计
基于statsmodels的实现方式
statsmodels中的统计描述对数据格式的要求更严格,但功能更强
DescrStatsW类不仅可以用于进行变量的统计描述,更是进一步进行各种比较的基础对象
from statsmodels.stats import weightstats as ws
des = ws.DescrStatsW(ccss.loc[:, ['index1', 'index1a', 'index1b']])
des.nobs # 无参函数不能写括号,否则报错
des.quantile([.05, .1, .5, .9, .95])
print(des.mean)
des.var
des = ws.DescrStatsW(ccss) # 混入字符串变量时会出错
des.var
分类变量的描述统计
单变量的频数统计
Series.value_counts(normalize = False : 是否返回构成比而不是原始频数sort = True : 是否按照频数排序(否则按照原始顺序排列)ascending = False : 是否升序排列bins : 对数值变量直接进行分段,可看作是pd.cut的简便用法dropna = True : 结果中是否包括NaN
)
ccss.time.value_counts()
ccss.s3.value_counts() # 数值变量也可直接列出频数表
ccss.s3.value_counts(bins = 20)
ccss.s5.value_counts(True) # “职业类型”的构成比
ccss.s5.value_counts().plot.bar() # 条形图
ccss.s5.value_counts().plot.pie() # 饼图
交叉表
pandas的crosstab命令可以完成基本的制表任务,但是和统计软件中的同类命令不同,缺少进行行列变量关联性检验的功能,这方面的任务需要使用statsmodels完成
pd.crosstab(ccss.s2, ccss.s0)
pd.crosstab(ccss.s2, ccss.s0, normalize = 0, margins = True) # 百分比,并计算相应的合计
pd.crosstab([ccss.s2, ccss.O1], ccss.s0)
pd.crosstab(ccss.s2, ccss.s0).plot.bar() # 条形图
pd.crosstab(ccss.s2, ccss.s0).plot.bar(stacked = True) # 堆积条形图
pd.crosstab(ccss.s2, ccss.s0, normalize = 0).plot.bar(stacked = True) # 百分堆积条图
总体与样本
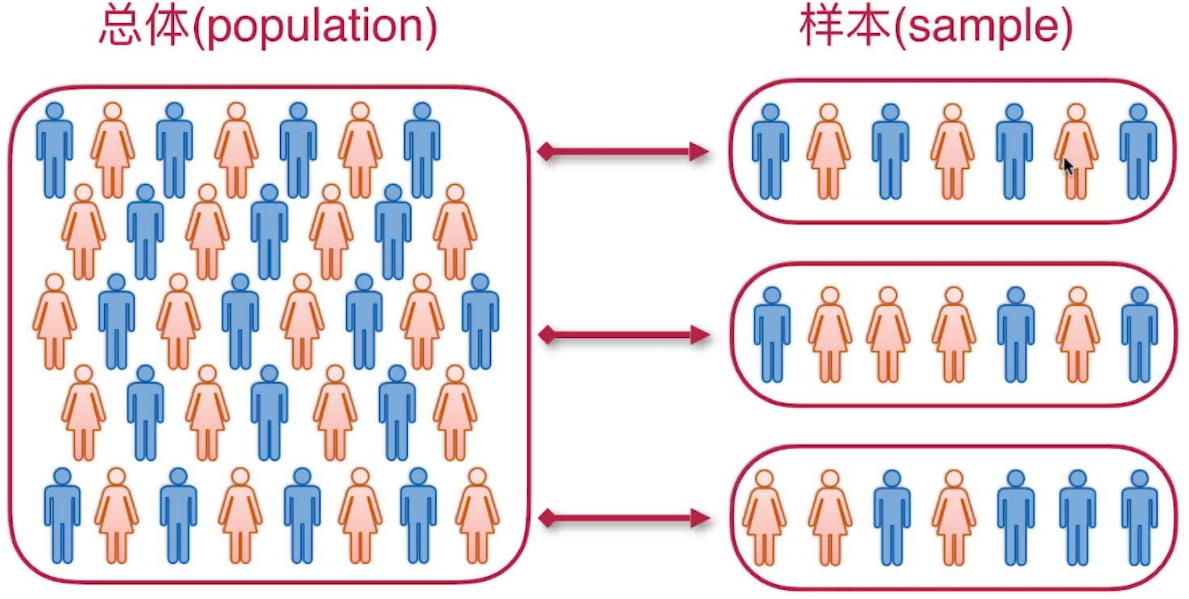
在实际中,总体的分布一般是未知的,或只知道它具有某种形式而其中包含着未知参数。这时,常用的办法就是根据样本来推断总体。
总体、个体、样本
- 总体:通常把研究对象的全体称为总体,一个总体对应于一个随机变量X
- 个体:把组成总体的每个成员称为个体
- 样本:在相同的条件下对总体X进行n次重复的、独立的观察,将n次观察结果按试验的次序记为X~1~,X~2~,...X~n~, 那么,称n维随 机变量(X~1~,X~2~,...X~n~)为样本,n为样本容量
注意:
样本(X~1~,X~2~,...X~n~)具有下列两个特性:
- 代表性 每一个X~i~ 应该与总体X 有相同的分布,i=1,...,n;
- 独立性 X~1~,X~2~,...X~n~应该是相互独立的随机变量
抽样分布
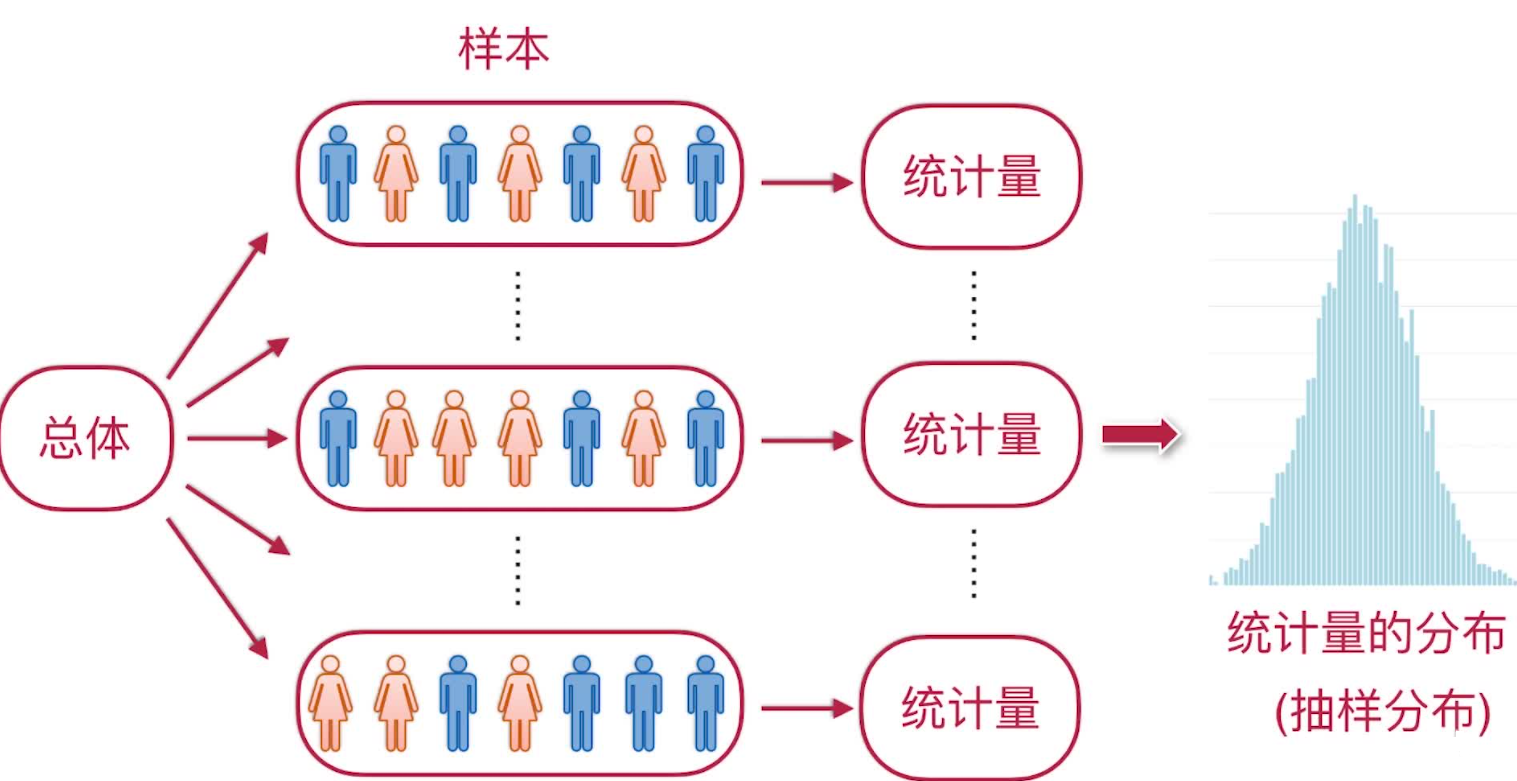
我们往往不是直接使用样本本身,而是针对不同的问题构造样本的适当函数,利用这些样本的函数(统计量)进行统计推断
统计量的概念
(X~1~,X~2~,...X~n~)是来自总体X 的一个样本,g(X~1~,X~2~,...X~n~)是(X~1~,X~2~,...X~n~)的函数,若g中不含未知参数,则称g(X~1~,X~2~,...X~n~)是一个统计量。
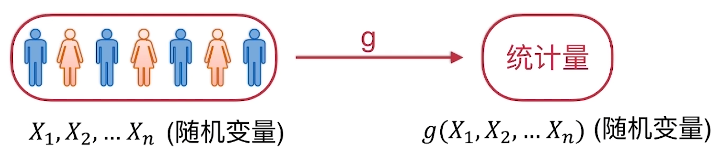
常用的统计量
X~1~,X~2~,...X~n~是来自总体X 的一个样本,则:
称
X¯=1n∑i=1nXi
为样本均值
称
S2=1n−1∑i=1n(Xi−X¯)2
为样本方差
称
S=1n−1∑i=1n(Xi−X¯)2
为样本标准差
抽样分布
由于统计量是样本的函数,从而一个统计量也是一个随机变量。把统计量的分布就叫做抽样分布。
注意:
通过对统计量的分布(抽样分布)进行分析,可以得到关于总体的未知信息。
常用统计量的分布在下一小节会讲到
三个常用的抽样分布
卡方分布
设X~1~,…,X~n~是独立同分布的随机变量,且都服从N(0,1)。称随机变量
Y=Σi=1nXi2
所服从的分布为自由度为n的卡方分布,记作
Y∼χ2(n)
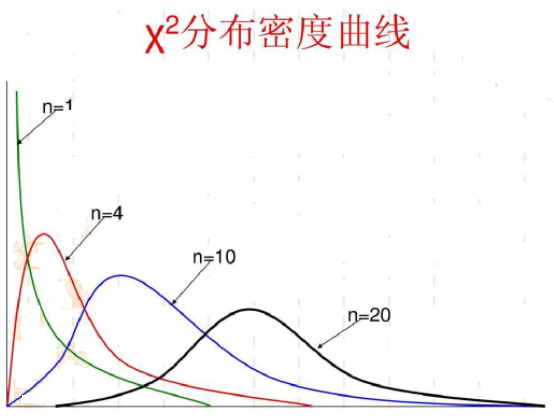
卡方分布的性质:
- 可加性
并且相互独立,则有χ12∼χ2(n1),χ22∼χ2(n2),并且χ12,χ22相互独立,则有χ12+χ22∼χ2(n1+n2)
- 期望和方差
E(χ2)=n,Var(χ2)=2n
t分布
设随机变量X与Y相互独立,且X~N(0,1), Y~χ2(n).称随机变量
T=XYn
所服从的分布为自由度为n的t分布(或学生分布),记作
T∼t(n)
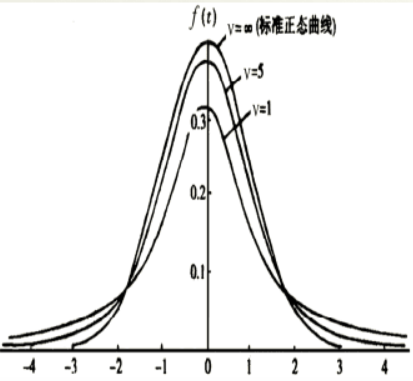
t分布密度函数的特点:
- t 分布曲线是关于 t=0 对称的单峰曲线
- 随着自由度增大,曲线逐渐接近正态分布;分布的极限为标准正态分布
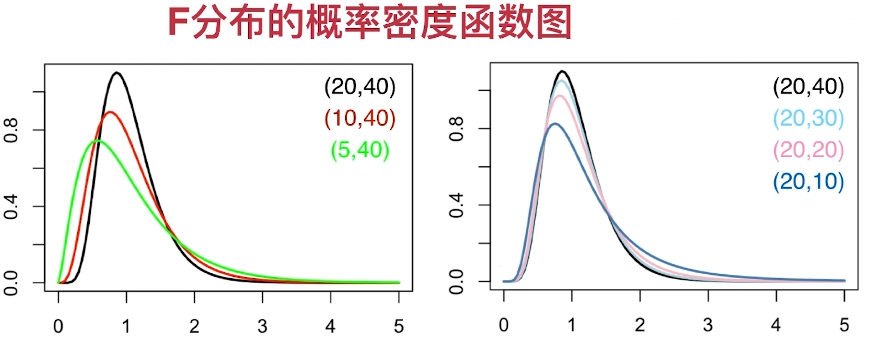
F分布
设随机变量X与Y相互独立,且X~χ2(m), Y~χ2(n).称随机变量
F=X/mY/n
所服从的分布是自由度为(m,n)的F分布,记作
F∼F(m,n)
正态总体的样本均值和样本方差的分布

基础定理:
设总体X的均值为μ,方差为σ^2^, X~1~,X~2~,...X~n~是来自总体X 的一个样本,
X¯,S2
分别为样本均值和样本方差.则有,
E(X¯)=μ,Var(X¯)=σ2nE(S2)=σ2
注意:
在这个基本定理中,并没有限定总体X的分布
前提条件:
X~1~,X~2~,...X~n~是来自正态总体N(μ,σ^2^)的一个样本,
X¯,S2
分别为样本均值和样本方差.
定理一:
X¯∼N(μ,σ2n)
定理二:
与相互独立(n−1)S2σ2∼χ2(n−1)X¯与S2相互独立
定理三:
X¯−μS/n∼t(n−1)
