巧用Bitset！优化dp

有关bitset的一些基本运用，请大家阅读这篇博客：
位图–Bitset【0基础详细版】
如果还想了解下位运算的话，可以看这篇博客：
位运算【入门–＞精通】

接下来我们要谈谈关于如何用bitset优化动态规划DP问题？

bitset是 C++ 标准库中的一个容器，用于高效存储和操作布尔值数组。它通过位运算将多个布尔状态压缩到一个或多个 32 位整数中，从而显著提升动态规划的时空效率。

用bitset优化动态规划的核心原理在于利用位运算的高校性，将原本时间复杂度为O(n)转化为O(n/32)或O(n/64).

原理

传统dp瓶颈

下面以经典的01背包问题为例：

• 状态：dp[j]表示能否组成j.
• 转移：dp[j]=max(dp[j],dp[j-v]).
• 时间复杂度：O(n*m)
• 空间复杂度：O(m)
• 缺点：当m很大时，循环次数多，且每个状态占1字节（8位），浪费空间！

bitset优化思路

状态压缩：用一位表示一个状态，空间能压缩8倍

• 传统数组：每个状态占 1 字节（8 位），如bool dp[1000000]需 1MB 内存。
• Bitset：每个状态占 1 位，bitset<1000000> dp仅需 125KB 内存。

位运算加速：一次位运算能处理32位，时间复杂度降为O(n*m/32)

• 左移操作：dp << v 等价于将所有可达的和加上 v。
• 按位或：dp |= … 将移动后的结果与原状态集合进行按位或操作,能快速合并多个状态集合。

什么？不太能看懂？模模糊糊？感觉很抽象？没关系没关系，初学时是很难理解，不过，有下面这个例子，相信你一定会豁然开朗！

经典例题：NC17193

简单瞎搞题


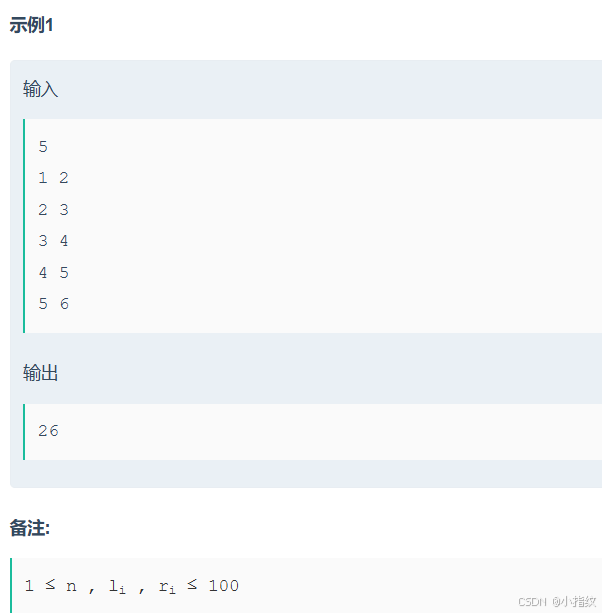
题目大意

给出n个区间，每次可以选区间中的任意一个数xi,然后求得$S=\sum x_i^2$，让你求这个s能有多少种？

思路

暴力枚举不可行：每个数有多个选择，直接枚举所有组合的时间复杂度是指数级的（最坏情况下每个区间长度为 100，5 个数就有 100^5 种组合）
动态规划思路：我们需要记录前 i 个数能组成的所有可能和，然后加入第 i+1 个数时更新这些和。但传统 DP 数组存储所有可能和会导致超时（时间复杂度 O (n * sum (ri))）
优化关键：利用 bitset 的位运算特性，将状态转移从 O (n) 优化到 O (n/32)，同时压缩空间

AC代码展示

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5;
int n,l,r;
bitset<N>dp,dt;
signed main()
{cin>>n;dp[0]=1;//表示1是可得的 while(n--){cin>>l>>r;dt.reset();//每有新的一组数，就要将初始置为0. for(int i=l;i<=r;i++){                  //或（|）运算，只要有一个1就为1；//不懂的后面会有详细的解释，一定要继续往下看。 dt|=dp<<(i*i); //相当于原来的和加上i*i（<<左移i*i,相当于加i*i) } dp=dt;//遍历完一个区间后要更新dp值 }//dp的第i为是1，表示i是可相加得到的和，pt中有多少1就相当于有几种和 cout<<dp.count();//输出dp中1的个数即S的种类数。return 0; 
}

代码解释

1. 初始 dp 的含义

假设 dp 是一个 10位的 bitset，每一位代表一个和是否可达：

Bit 位置: 9 8 7 6 5 4 3 2 1 0
dp 的值:  0 0 0 0 0 1 0 1 1 0

• dp[0] = 0：和为 0 不可达
• dp[1] = 0：和为 1 不可达
• dp[2] = 1：和为 2 可达
• dp[3] = 1：和为 3 可达
• dp[4] = 0：和为 4 不可达
• dp[5] = 1：和为 5 可达
• dp[6] = 0：和为 6 不可达
• dp[7] = 0：和为 7 不可达
• dp[8] = 0：和为 8 不可达
• dp[9] = 0：和为 9 不可达

所以 dp = 0000010110 表示和 {2,3,5} 可达。

---

2. dp << 4 的含义

dp << 4 表示将 dp 的所有位 左移 4 位，低位补 0：

原 dp:        0 0 0 0 1 0 1 1 0
左移 4 位:    1 0 1 1 0 0 0 0 0

所有可达的和 + 4：

• 原 dp 表示和 {2,3,5} 可达。
• 左移 4 位后：
  • 和 2 → 2 + 4 = 6（dp[6] = 1）
  • 和 3 → 3 + 4 = 7（dp[7] = 1）
  • 和 5 → 5 + 4 = 9（dp[9] = 1）

所以 dp << 4 的结果应该是：

Bit 位置: 9 8 7 6 5 4 3 2 1 0
新 dp:    1 0 1 1 0 0 0 0 0 0

3.dp|=...的含义

dp |= …是指将移动后的结果与原状态集合进行按位或操作
按位或（ | ）：只有都为0时才为0，只要有一个1就是1.
所以,就算用不同选择的方式相加得到的和相同，即不会重复计算也不会漏算，这一位为1就一直是1了。

4.dp.reset()和dp.count()的含义

dp.reset() 表示清空指定位或所有位，将其设为0
dp.count() 表示获取被设置为1的位的个数（即1的数量）
更多详细函数可参考一下：

看到这里你一定理解掌握了吧，这有一道热乎的同类型的题，让我们一起去练习吧~

相关例题推荐

小红组比赛

小红组比赛


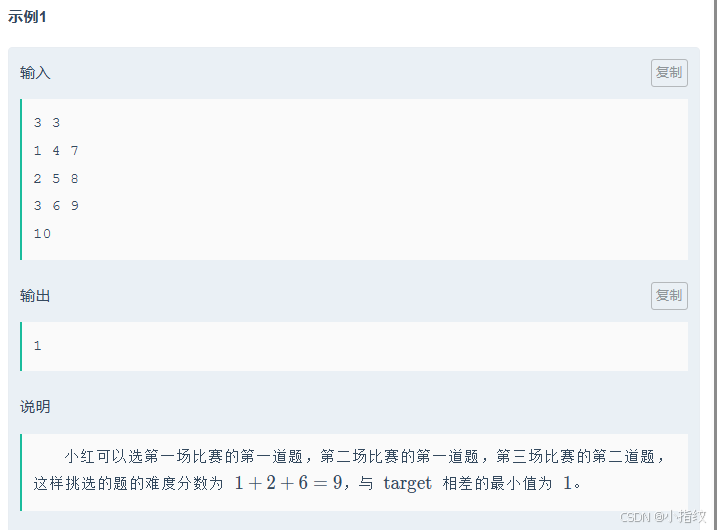
思路

这道题和上一道很相似，我们可以先算出一共有多少种，然后再找出差值最小的那个输出即可。由题目给出的范围可知，最多有5000种可能的分数，所以直接遍历的话不会超时。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=5055;
int n,m,x;
bitset<N>b,t; 
void solve()
{cin>>n>>m;b.set(0);//初始化为0 while(n--)//计算出所有情况 {t.reset();for(int i=1;i<=m;i++){cin>>x;t|=b<<x;}b=t;}int tg,ans=INT_MAX;cin>>tg;for(int i=0;i<5050;i++)//一共就5000中可能的分数，所以直接遍历即可不会超 {if(b[i])ans=min(ans,abs(i-tg));}cout<<ans;
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

关于bitset优化dp,求总共多少情况类型的题，可以参考这个模板：

bitset的核心步骤bitset<N> b, t;b.set(0);for(int i = 1; i <= n; i ++ ) {t.reset();for(int j = 1; j <= m; j ++ ) {int x; cin >> x;t |= (b << x);}b = t;}