数据结构第八章（五）-外部排序和败者树

---

外部排序和败者树

一、外部排序

首先，没说之前，在开始，All of the first，我们要知道的是，外存、内存之间是怎么进行数据交换的。

看这里：

左边就是我们的外存，可以看到里面放了很多的磁盘块；右边是我们的内存，空间要比外存小很多。

我们内存和外存之间的数据交换的最小单位就是磁盘块，一个块一个块进行交换

即 磁盘的 读/写 以“块”为单位，数据读入内存后才能被修改，修改完了还要写回磁盘 ，就是这样：

可以看到我们把存放“8 12 7”的磁盘块读入了内存。

我们就可以在内存中进行修改，把它修改成“1 2 3”，再写回磁盘（注意，此时是随机写入，而不是一定在读入的那一个磁盘块里），这样才算是修改完成。

所谓的外部排序就是：我们的元素很多，我们没办法把这些存放在磁盘中的数据全部都读入内存中，所以把它们存放在磁盘中。我们要对在外存中的这些数据进行排序，这就是外部排序了。

我们外部排序采用 “归并排序” 的方法

好，我们刚知道我们外部排序是用“归并排序”来操作，但是我们要用“归并排序”是有前提的。

还记得我们“归并排序”有什么前提要求吗？

“归并排序”要求各个子序列有序

但是我们放在外存中的肯定不是有序的，所以我们就要进行初始化操作，也就是构造初始归并段

简单来说，就是先打造我们进行“归并排序”需要的条件。我们 每次读入两个块的内容，进行内部排序后写回磁盘：

1.构造初始归并段

我们现在打算进行的初始化是：每次读入两个块，排好序再读出，让磁盘中的块两个两个有序

我们最少只需在内存中分配3块大小的缓冲区即可对任意一个大文件进行排序：

可以看到，我们内存中开了三个缓冲区，两个是输入缓冲区，一个是输出缓冲区。

我们现在要让它们两两有序。所以我们要先把两个块读入内存中，即（我们下面都是宏观描述一下）：

我们对着两个 输入缓冲区块 一起进行排序：

现在我们要写回磁盘，所以我们把输入缓冲区1的数据放入输出缓冲区中，即：

我们写回磁盘，再把输入缓冲区2的数据放入输出缓冲区中，即：

再写回磁盘，我们的一个有序的“归并段”就完成了：

我们再把两个块读入内存中，即：

我们对着两个 输入缓冲区块 一起进行排序：

现在我们要写回磁盘，最后的结果就是这样：

以此类推……我们最终得到的就是这样：

那么我们的初始归并段就构造完成了。

我们一共 16 个块，每次都需要把块读入内存中，然后把排好序的块再读出来，平均每个块都要被读一次写一次，所以构造初始归并段需要进行16次读和16次写。

2.归并排序

现在我们进入正题，我们来对它们进行归并排序。

我们上面已经构造了 8 个有序的子序列，所以：

第 1 趟归并，把 8 个有序子序列（初始归并段）两两归并

我们的 归并段1 和 归并段2 如下，并且我们开辟一片和两个有序子序列一样大的空间用来存放两个有序子序列进行“归并排序”后的有序序列：

现在我们把 归并段1 和 归并段2 中分别取序列中小的 1 块读入内存中：

刚刚读入内存的输入缓冲区中的显然已经是排好序的，我们 再按照“归并排序”的过程 ，即指针 i 和指针 j 分别指向 输入缓冲区的两个块，然后再选出小的放到输出缓冲区中

如果是选的是 指针 i 指向的，那就指针 i 往后挪一格接着比接着选，如果选的是 指针 j 指向的也同理

那么就是这样，输出缓冲区填满了：

现在我们写到我们针对这 两个归并段 排序后的序列中：

现在 我们 再按照“归并排序”的过程 ，即指针 i 和指针 j 分别指向 输入缓冲区的两个块，然后再选出小的放到输出缓冲区中，发现输出缓冲区放了 2 个元素后，输入缓冲区1 空了：

哪个缓冲区空了，就要从相对应的归并段中再读出1块补上（缓冲区1对应归并段1，缓冲区2对应归并段2），我们补上再进行“归并排序”：

输出缓冲区又填满了，我们再 写到我们针对这 两个归并段 排序后的序列中：

可以看到现在 缓冲区2 也空了，哪个缓冲区空了，就要从相对应的归并段中再读出1块补上（缓冲区1对应归并段1，缓冲区2对应归并段2）：

我们再进行“归并排序”（过程不再赘述，也就是上面的橙色字），发现 输出缓冲区又填满了：

我们再 写到我们针对这 两个归并段 排序后的序列中：

我们再再进行“归并排序”（过程不再赘述，还是上面的橙色字），发现 输出缓冲区又填满了：

我们最后再 写到我们针对这 两个归并段 排序后的序列中：

那么我们就完成了将两个有序归并段归并为一个这个过程，即我们把两个归并段归并成了一个更长的有序序列：

我们一共 8 个初始归并段，现在对每两个进行这个过程操作，即进行 4 次，就变成了 4 个有序的子序列：

我们的第 1 趟归并就完成了。

那么现在，我们可以进行更进一步操作了。

我们上面已经构造了 4 个有序的子序列，所以：

第 2 趟归并，把 4 个有序子序列（初始归并段）两两归并

我们的 归并段1 和 归并段2 如下：

我们开辟一片和两个有序子序列一样大的空间用来存放两个有序子序列进行“归并排序”后的有序序列：

现在我们把 归并段1 和 归并段2 中分别取序列中小的 1 块读入内存中：

刚刚读入内存的输入缓冲区中的显然已经是排好序的，我们 再按照“归并排序”的过程 ，即指针 i 和指针 j 分别指向 输入缓冲区的两个块，然后再选出小的放到输出缓冲区中

如果是选的是 指针 i 指向的，那就指针 i 往后挪一格接着比接着选，如果选的是 指针 j 指向的也同理

那么就是这样，输出缓冲区填满了：

现在我们写到我们针对这 两个归并段 排序后的序列中

接着我们 再按照“归并排序”的过程 ，即指针 i 和指针 j 分别指向 输入缓冲区的两个块，然后再选出小的放到输出缓冲区中，发现输出缓冲区放了 2 个元素后，输入缓冲区1 空了：

哪个缓冲区空了，就要从相对应的归并段中再读出1块补上（缓冲区1对应归并段1，缓冲区2对应归并段2），我们补上再进行“归并排序”：

输出缓冲区填满了，我们写到我们针对这 两个归并段 排序后的序列中：

可以看到现在 缓冲区2 也空了，哪个缓冲区空了，就要从相对应的归并段中再读出1块补上（缓冲区1对应归并段1，缓冲区2对应归并段2）：

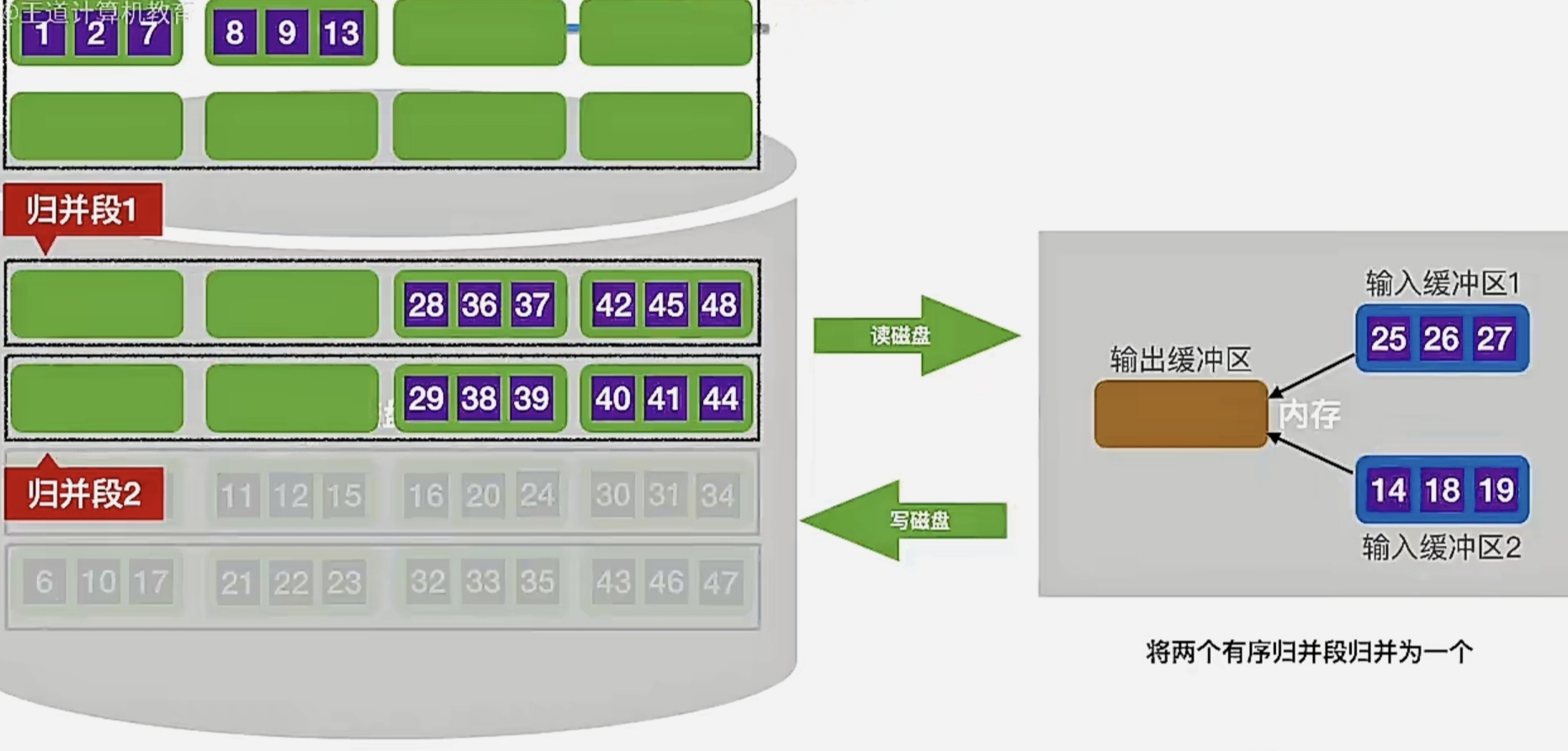
以此类推……我们最终对这两个归并段进行完“归并排序”就是这样的：

那么我们就又完成了将两个有序归并段归并为一个这个过程，即我们把两个归并段归并成了一个更长的有序序列：

下面的两个归并段也按照上述这样操作，结果就是这样：

我们一共 4 个初始归并段，现在对每两个进行这个过程操作，即进行 2 次，就变成了 2 个有序的子序列：

那么我们的第 2 趟归并就完成了。

那么现在，我们可以进行更进一步操作了。

我们上面已经构造了 2 个有序的子序列，所以：

第 3 趟归并，把 2 个有序子序列（初始归并段）两两归并

过程不再赘述，结果是这个样子的：

可以看到，经过 3 趟归并，在磁盘中的数据已经整体有序了，我们的外部排序就完成了。

3.效率影响因素

由于我们每次内存读写都是以“块”为单位的，所以我们其实生成初始归并段和每一趟归并都要分别读写“16”次

初始化后生成 8 个初始归并段，每个段占 2 块

• 第一趟归并生成 4 个初始归并段，每个段占 4 块
• 第二趟归并生成 2 个初始归并段，每个段占 8 块
• 第三趟归并生成 1 个初始归并段，每个段占 16 块，此时已经是有序的了

总体来看就是这样：

我们先要初始化排序，还要进行归并，这其中还穿插着读写外存

所以我们的 外部排序时间开销 = 读写外存的时间 + 内部排序所需的时间 + 内部归并所需的时间

当然显然，“读写外存的时间”肯定占大头。所以如果我们想要优化，这个“读写外存的时间”就得优先称为优化的点。

我们刚刚的过程中，

初始化的时候读写 16 * 2 = 32 次

第一趟排序中 每次合并2个归并段（一个归并段 2 块）需要读写 4 * 2 次，一共 4 次，所以需要 4 * 2 + 4 * 2 + 4 * 2 + 4 * 2 = 32次；

第二趟排序中，每次合并 2 个归并段（一个归并段 4 块）需要读写 8 * 2 次，一共 2 次，所以需要 8 * 2 + 8 * 2 = 32次；

第三趟排序中，每次合并 2 个归并段（一个归并段 8 块）需要读写 16 * 2 次，一共 1 次，所以需要 16 * 2 = 32次；

即 刚刚的过程 需要进行 3 趟归并，读、写磁盘次数 = 32 + 32 * 3 = 128次

4.优化：多路归并

刚刚用的“归并排序”，其实显然就是“2路归并”。

我们不是只在内存中开了两个输入缓冲区吗，现在我们不开两个了，开四个（就是变成“4路归并”）：

这样的话，我们一次就可以进行 4 个 归并段的合并了，归并段1，归并段2，归并段3，归并段4 都可以有1块被读入内存中了，最后合并会直接变成一个 里面有 4 个归并段 的大归并段

所以我们对 前4个 归并段进行 4路归并，对 后4个 归并段进行 4路归并，即第1趟归并完成后，就会生成 2个 大归并段，也就是下面这样：

此时我们有 2 个归并段，只需要再进行一趟归并就可以完成我们外部排序了。

所以过程就变成了这样，只需要2趟：

我们现在读写次数就是

初始化的时候读写 16 * 2 = 32 次

第一趟排序中 每次合并4个归并段（一个归并段 2 块）需要读写 8 * 2 次，一共 2 次，所以需要 8 * 2 + 8 * 2 = 32次；

第二趟排序中，每次合并 2 个归并段（一个归并段 8 块）需要读写 16 * 2 次，一共 1 次，所以需要 16 * 2 = 32次

即 采用 4 路归并，只需要进行 2 趟归并，读、写磁盘次数 = 32 + 32 * 2 = 96次

这比刚刚“2路归并”中的 128 次少了不少，所以我们可以得出：

采用多路归并可以减少归并趟数，从而减少磁盘 I/O （读写）次数

对 r 个初始归并段，做 k 路归并，则归并树可以用 k 叉树表示

我们 k 叉树 第 h 层最多有 k^h-1 个结点，则 r ≤ k^h-1，（h-1）_最小 = ⌈ log_kr ⌉

所以 若树高为 h，则归并趟数 = h-1 = ⌈ log_kr ⌉

由此我们得知， k 越大，r 越小，归并趟数越少，读写磁盘次数越少

增加 k 确实读写磁盘次数少了。但是！！！也不是说我们4路比2路归并读写磁盘次数少，归并路数就越多越好的，k 也不能一直增大。多路归并带来的负面影响：

1. k 路归并时，需要开辟 k 个输入缓冲区，内存开销增加
2. 每挑选一个关键字需要对比关键字 (k-1) 次，内部归并所需时间增加

第一条说的很显然，第二条也是我们在归并排序也说过的，k 路归并每挑选一个关键字就要对比 (k-1) 次。

那么这个有没有什么优化的地方呢？答案是有的，这也就是我们下面要说的“败者树”，可以让它们不对比 (k-1) 次就能挑选出关键字。

那我们 r 呢？我们 r 是 r 个初始归并段，是我们在一开始构造的那个。那么我们怎么 减少 r 呢？

我们在构造的时候不是借助了两个输入缓冲区嘛，但是如果我们缓冲区大一点，每个初始归并段的长度会增加，生成的初始归并段可能就个数会减少，即：

生成初始归并段的“内存工作区”越大，初始归并段越长。

所以如果能增加初始归并段的长度，则可以减少初始归并段的数量 r 。若一共有 N 个记录，内存工作区可以容纳 L 个记录，则初始归并段数量 r = N/L。

-----小拓展-----

我们所说的 “多路平衡归并” 和 “多路归并” 有什么区别呢？

我们来看下面这个：

这个就是一个典型的，它是“4路”归并排序，但是它不是“4路”平衡归并排序。

为什么呢？我们看第一行，是不是其实 R1、R2、R3、R4 可以像 R5、R6、R7、R8 一样合并为一个，但是它没有，所以不“平衡”（当然这是我自己的理解哈）

即：k 路 平衡归并必须满足：

• 最多只能有 k 个段归并为 1 个
• 每一趟归并中，若有 m 个归并段参与归并，则经过这一趟处理得到 ⌈ m/k ⌉ 个新的归并段

那我们再回过头来看上面那个图，它 8 个归并段经过一趟处理后得到 3 个新的归并段，但是 ⌈ 8/3 ⌉ = 2 ≠ 3 ，所以它是“4路”归并排序，但不是“4路”平衡归并排序。

二、败者树

我们知道，在归并排序中，k 路归并每挑选一个关键字就要对比 (k-1) 次

如果是“8路”归并的话，那从8个归并段中选出一个最小元素就需要对比 7 次，这样内部归并所需的时间就大大增加

看着是不是就很恐怖：

但是“败者树”可以让它们不对比 (k-1) 次就能挑选出关键字。

我们来看什么是败者树，参考别人举的一个例子，我没看过这个动漫，但是这例子很通俗易懂：

看出来了吗？失败者留在这一回合，胜利者进入下一回合比拼，最终只有一个冠军在所有比赛中获胜。

简单来说就是选出武力值最高的，先两两进行对比，输了的记录下来，赢了的继续向上两两对比，输了的再记录下来……直到最后只剩两个人，它俩比，输了的再记录下来（就变成这个树的根了），最终赢了的那个在根往上一层。

这就是我们的败者树。

如果有 8 个参赛者，需要进行 7 次比拼，才能构造关于这 8 个参赛者的“败者树”

1.构造败者树

其实我们已经知道什么是败者树了，我们来看一下它的定义：

败者树——可视为一个完全二叉树（多加了一个头头）。

k 个叶结点分别是当前参加比较的元素，非叶子结点分别是当前参加比较的元素，非叶子结点用来记忆左右子树中的“失败者”，而让胜者往上继续进行比较，一直到根结点。

那么它有什么用呢？我们还是拿上面漫画的那个举例来看，我们已经有了那样一棵败者树。

我们已经知道了冠军叫什么饭，那现在这个饭不参加比赛了，由派大星来顶替它，那么现在派大星是不是只需要和阿乐比，如果赢了就继续往上和程龙比，如果再赢就和孙悟空比，如果再赢就是第一了是吧。当然输了就留在这，让另一个人接着往上比，一样的。

所以你看，我们右半部分都没有比，就能选出来冠军，这是不是不需要比 7 次了，只需要比 3 次就可以了

基于已经构建好的败者树，选出新的胜者只需要进行 3 场比赛

情况是在和孙悟空比的时候输了，所以留在孙悟空的位置：

这就是我们“败者树”的意义所在了。

2.败者树的应用

我们已经会构建败者树了，那么败者树在多路平衡归并中有什么应用呢？

我们现在来讨论“8路”归并的情况，现在我们有 8 个归并段，我们先在每个归并段中取出一个：

可以看到，我们每个叶子结点对应一个归并段中的数。

那么我们现在用 分支结点 来记录 失败者来自哪个归并段 ，用 根节点 来记录 冠军来自哪个归并段

注意，是记录来自哪个归并段，而不是把自己记上。

经过对比及记录，结果就是这样：

可以看到，我们构造这一棵败者树的时候，还是免不了要进行 7 次对比。

对于 k 路归并，第一次构造败者树需要对比关键字 k-1 次

我们选出了我们这棵败者树的冠军，也就是来自 归并段3 的元素，我们发现它是 “1”

我们把它取出：

由于是从 归并段3 中取出的，所以我们再从 归并段3 中取出一个补上：

现在，新元素“6”需要重新进行对比。

先和 归并段4中元素比，发现 6<17，“6”胜出；

再继续往上比，和 归并段2 中元素比，发现 6<12，“6”又胜出；

再继续往上比，和 归并段5 中元素比，发现 6>2，“6”失败，所以留下它的来历，把 归并段3 记录在这，归并段5 中元素胜出

也就是这样：

可以发现只对比了 3 次。

那么我们再把胜者也就是现在最小的元素从 归并段5 中拿出来，再从 归并段5 中取出元素顶替，以此类推……………………（这里不再赘述，上面说的能明白就可以了）

所以！有了败者树，我们选出最小元素，只需要对比关键字 ⌈log₂k⌉ 次

其实就是这个败者树的树高啦（当然不包括根节点头上的那个结点）。

看起来“8路”归并之前要对比 7 次，现在要对比 3 次，减少的程度很少，但是如果我们是“1024路”归并，那有了败者树就可以只对比 10 次，没有就需要对比 1023 次，我们败者树优化地还是很明显的。

-----拓展-----

当然如果想用代码实现我们的败者树的话，k 路归并 定义一个大小为 k 的数组就可以了，也就是这样：

可以看到我们叶子结点是“虚拟的”，也可以看到我们数组中存放的其实就是完全二叉树的存放方式，把每个结点的值都存在这个数组里，下标为0的存的就是根结点上面的那个冠军结点了。

那么我们书上举的例子是“5路”归并的败者树，也就是这个样子的：

可以看到，如果我们 b₁ 或 b₂ 归并段中的元素是最小的，那么下次从 这归并段中取出元素，其实只需要对比 2 次就可以了。我们又说对比次数是 ⌈log₂5⌉ = 3 ，不是2，这是怎么回事呢？

其实也就是，我们所说的 ⌈log₂k⌉ 是它对比的上限，而非表示我们一定对比这么多次。就像书上的例子，可能对比 3 次也可能对比 2 次，是吧。

---

总结

外部排序其实就是把磁盘中的数据读两块到内存中，然后再进行“归并排序”，使两个归并段变成一个有序的大归并段，注意这个前提条件是有序的子序列。

“败者树”其实就是让归并排序对比的时候不要对比那么多次，有很多其实是可以避免的，看看我们的树就很容易理解了。引入“败者树”，就可以让我们再多路平衡归并中对比次数从 k-1 减少到 ⌈log₂k⌉ ，效率就会高很多。