数据结构第八章（三）-选择排序

---

选择排序

---

选择排序，人如其名，就是选择一个然后放前面排序。

再简单来说，就是在最开始画一条线，每次都在线后面的元素中找到最小或者最大的放前面，放一个后挪一格，那么线前面的就都是有序的。这个线一个一个往后挪，直到挪到最后，线后面没东西了，我们的排序也完成了。

选择排序：每一趟在待排序元素中选取关键字最小（或最大）的元素加入有序子序列。

这就是选择排序。

一、简单选择排序

1.算法过程

用一个栗子来说简单选择排序，我们的待排序元素如下：

49(1)	38	65	97	76	13	27	49(2)
0	1	2	3	4	5	6	7

我们每一趟在待排序元素中选取关键字最小的元素加入有序子序列

我们肯定还是需要用到辅助指针，一个指针 i，一个指针 j。指针 i 从位置 1 开始，指针 j 遍历指针 i 后面的元素，找到最小的之后和指针 i 所在位置的元素进行交换。

第1趟

指针 i = 0 指向元素”49“，指针 j 遍历指针 i 后面的元素，从 位置 1 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 5，指向的元素为 “13”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	38	65	97	76	49(1)	27	49(2)
0	1	2	3	4	5	6	7

第2趟

我们指针 i 往后挪现在为 1 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“1~7”，指针 i 及 i 之后的部分

指针 i = 1 指向元素”38“，指针 j 遍历指针 i 后面的元素，从 位置 2 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 6，指向的元素为 “27”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	65	97	76	49(1)	38	49(2)
0	1	2	3	4	5	6	7

第3趟

我们指针 i 往后挪现在为 2 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“2~7”，指针 i 及 i 之后的部分

指针 i = 2 指向元素”65“，指针 j 遍历指针 i 后面的元素，从 位置 3 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 6，指向的元素为 “38”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	38	97	76	49(1)	65	49(2)
0	1	2	3	4	5	6	7

第4趟

我们指针 i 往后挪现在为 3 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“3~7”，指针 i 及 i 之后的部分

指针 i = 3 指向元素”97“，指针 j 遍历指针 i 后面的元素，从 位置 4 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 5，指向的元素为 “49”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	38	49(1)	76	97	65	49(2)
0	1	2	3	4	5	6	7

第5趟

我们指针 i 往后挪现在为 4 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“4~7”，指针 i 及 i 之后的部分

指针 i = 4 指向元素”76“，指针 j 遍历指针 i 后面的元素，从 位置 5 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 7，指向的元素为 “49”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	38	49(1)	49(2)	97	65	76
0	1	2	3	4	5	6	7

第6趟

我们指针 i 往后挪现在为 5 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“5~7”，指针 i 及 i 之后的部分

指针 i = 5 指向元素”97“，指针 j 遍历指针 i 后面的元素，从 位置 6 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 6，指向的元素为 “65”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	38	49(1)	49(2)	65	97	76
0	1	2	3	4	5	6	7

第7趟

我们指针 i 往后挪现在为 6 ，指针 i 之前的元素都是找到其最终位置的（排好序的），所以不用再管了。 现在的待排序元素是“6~7”，指针 i 及 i 之后的部分

指针 i = 6 指向元素”97“，指针 j 遍历指针 i 后面的元素，从 位置 7 开始 往后遍历，用一个临时变量min记录最小位置的下标，遇到比此时的 j 指向元素更小的就更新 min

遍历完之后我们发现 min 是 7，指向的元素为 “76”，我们再看它和指针 i
指向的元素相不相同，不相同就换，相同就不换。

发现不同，交换指针 i 和 指针 min 指向的元素：

13	27	38	49(1)	49(2)	65	76	97
0	1	2	3	4	5	6	7

现在待排序元素只剩最后一个了，不用再处理了。

所以我们发现，一共8个元素，第7趟排序就已经有序排完了

so n 个元素的简单选择排序需要 n-1 趟处理

刚刚我说的就是按照算法实现来说的，所以上代码就会发现异常清晰：

//交换
void swap(int &a, int &b){int temp = a;a = b;b = temp;
}//简单选择排序
void selectSort(int A[],int n){for(int i = 0; i < n-1; i++){       //一共进行 n-1 趟int min = 1;                    //记录最小元素位置for(int j = i+1; j<n; j++){     //在A[i……n-1]中选择最小的元素if(A[j] < A[min]){          //更新元素最小位置min = j;}}if(min != i){swap(A[i], A[min]);         //交换，封装的swap共移动元素3次}}
}

是吧。

2.性能

空间复杂度不用说了，显然是O(1)

那我们的时间复杂度该怎么说？

首先这个简单选择排序，

不论是有序、逆序还是乱序，都一定需要 n-1 趟处理

每一趟可能交换也可能不交换，所以元素总交换次数 ≤ n-1

总共需要对比关键字 (n-1) + (n-2）+ …… + 1 = n(n-1)/2 次

so 时间复杂度 = O(n²)

那它的稳定性如何？

比如我们的待排序序列为：2(1) 2(2) 1

那第1趟排序结束 肯定把最小的“1”换到最前面，所以就变成了 1 2(2) 2(1)

再进行第2趟排序，不是比指针 i 指向小的就不交换
所以最终排序结果为 1 2(2) 2(1)

故简单选择排序是不稳定的。

简单选择排序既可以适用于顺序表，也可以适用于链表。

二、堆排序

还记得我们选择排序是什么吗？

选择排序：每一趟在待排序元素中选取关键字最小（或最大）的元素加入有序子序列。

我们堆排序也是一种选择排序。

1.堆(Heap)

首先我们要堆排序，就得直到什么是“堆”。

若 n 个关键字序列L[1……n] 满足下面某一条性质，则成为堆（Heap）：

• 若满足： L(i) ≥ L(2i) 且 L(i) ≥ L(2i+1) （ 1 ≤ i ≤ n/2）—— 大根堆（大顶堆）
• 若满足： L(i) ≤ L(2i) 且 L(i) ≤ L(2i+1) （ 1 ≤ i ≤ n/2）—— 小根堆（小顶堆）

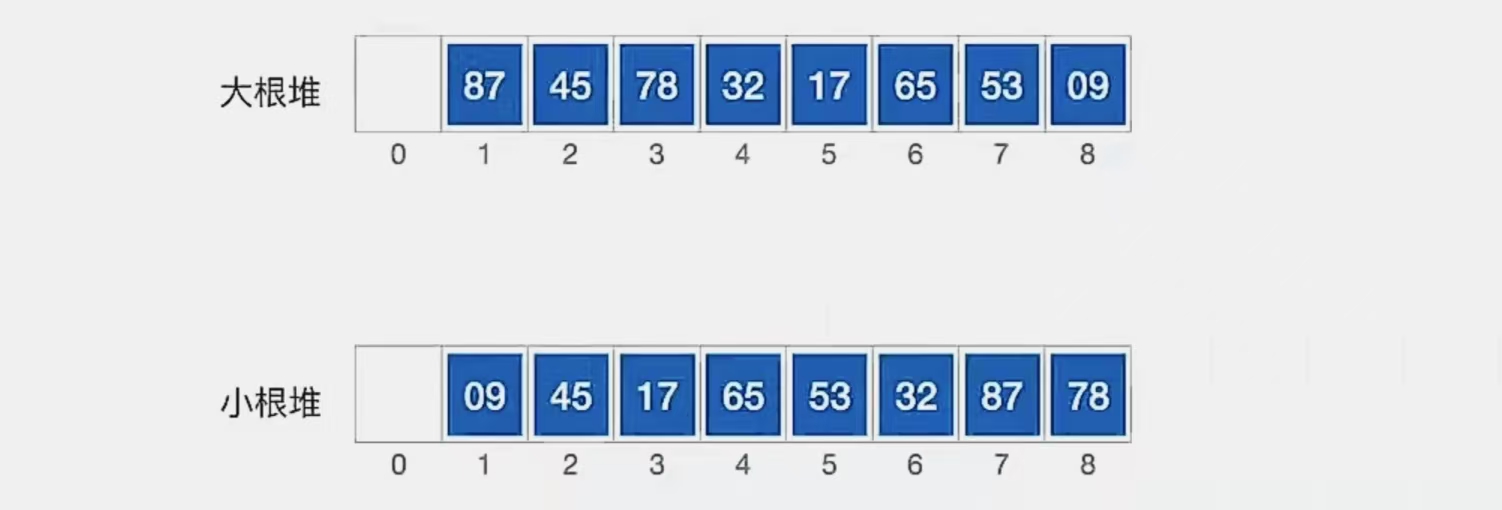
那么这个显然比较抽象，这是存储视角。我们怎么理解呢？其实理解成一棵树就好了，叶就是二叉树顺序存储。

大根堆就是所有双亲结点都比左、右孩子大的树，小根堆就是所有双亲结点都比左、右孩子小的树

逻辑视角如下：

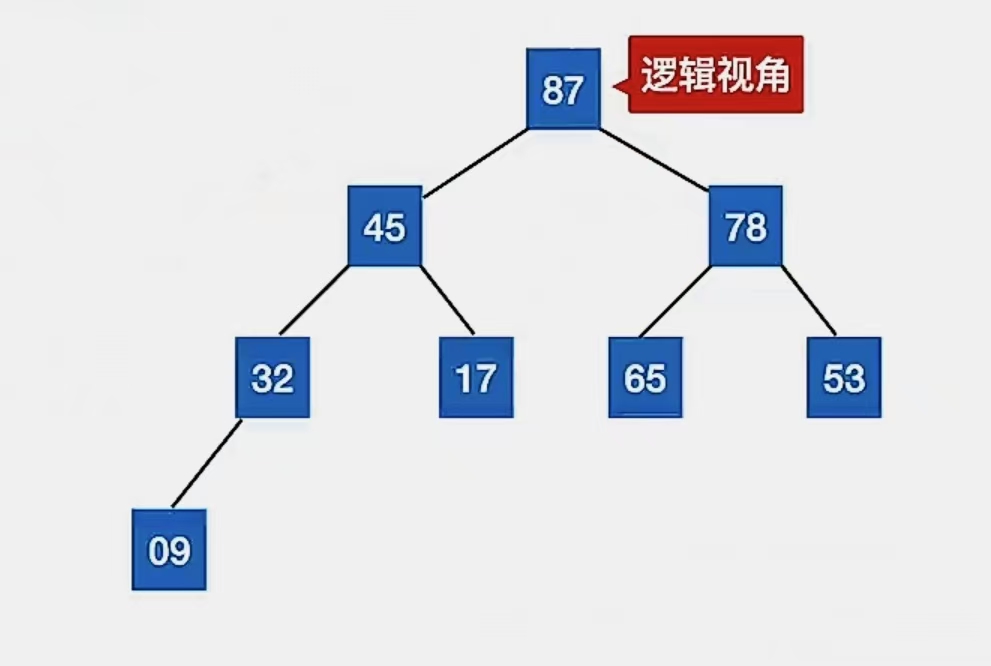
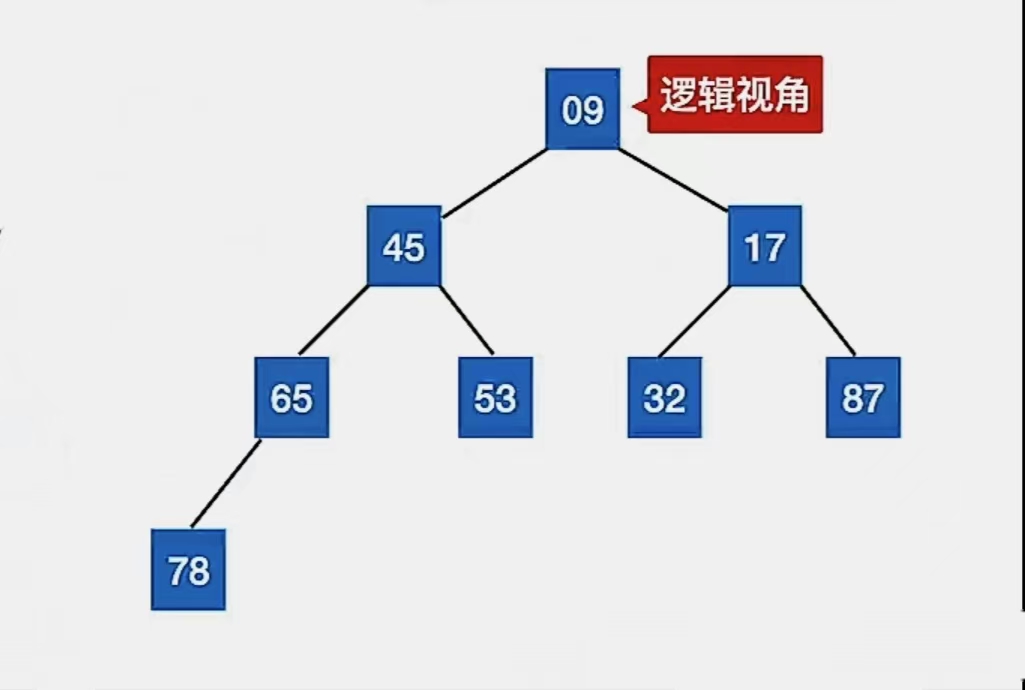
还记得我们的二叉树顺序存储吗？回顾一下

基本操作：

• i 的左孩子下标：2i
• i 的右孩子下标：2i+1
• i 的父结点下标：⌊i/2⌋
• i 所在的层次：⌈log2（n+1)⌉ 或 ⌊log2n⌋+1

若完全二叉树中共有n个结点，则

• 判断 i 是否有左孩子：看 2i ≤ n成不成立
• 判断 i 是否有右孩子：看 2i+1 ≤ n成不成立
• 判断 i 是否是叶子/分支结点：看 i ＞ ⌊n/2⌋ 成不成立

比较直观的就是打比方这个完全二叉树：

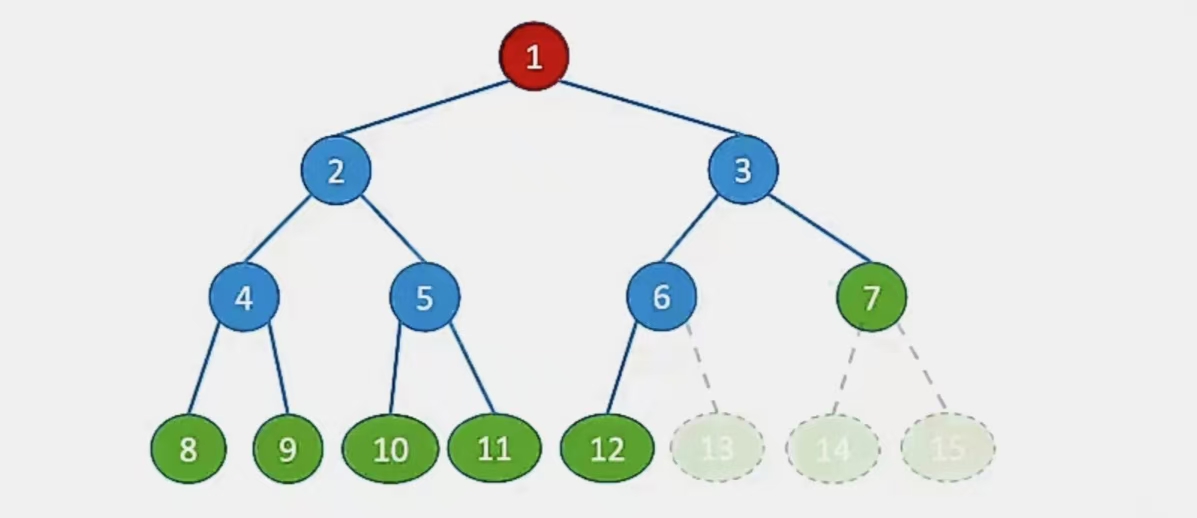
在顺序表中就是这样：

其中红色是根结点，绿色部分是叶子结点，红色和蓝色部分是非叶子结点。

我们要想找到非叶子结点，只需要找下标 i ≤ ⌊n/2⌋

回到正题。什么是堆？简单来说，就是

大根堆：完全二叉树中，根≥左、右；
小根堆：完全二叉树中，根≤左、右

多说一嘴，我们二叉排序树BST是左<根<右，堆和这个还是很不一样的。

那么我们知道什么是“堆”了，如果给我们一个“堆”，我们怎么进行选择排序？

选择排序不是每一趟都在待排序元素中选取关键字最小（或最大）的元素加入有序子序列吗？

那么我们有了“堆”之后，由于“堆”本身的性质，所以堆顶的元素一定是关键字最大（最小）的，所以待排序元素如果是一个“堆”，直接取堆顶元素就可以了，这样就非常地方便又快捷。

问题不会消失，只会转移，所以我们的问题现在就变成了怎么把待排序元素变成一个“堆”，也就是堆的建立。

2.堆的建立

我们还用一个栗子来讲，描述建立“大根堆”（根 ≥ 左、右）的过程。

首先给出我们的初始序列，及按照初始序列作为二叉树结点的顺序存放给出的二叉树如下：

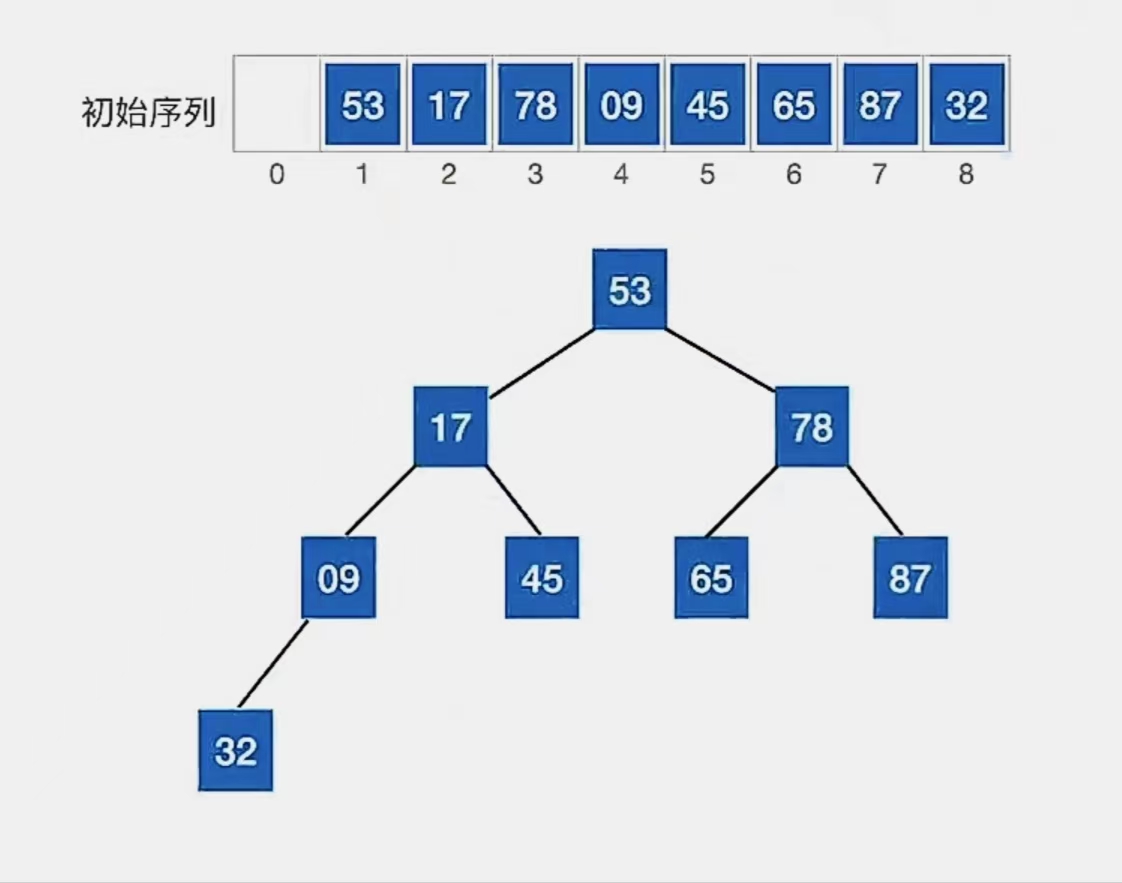
这显然不是一个大根堆。

所以我们就得 自底向上 把所有非终端结点都检查一遍，看是否满足大根堆的要求，如果不满足，则进行调整。

怎么调整？

我们知道“大根堆”肯定是满足 根≥左、右 的，不满足那就是根没有左右孩子大，所以我们就直接找到左、右孩子里面最大的那个，然后和根换就完了呗。

就是这样。

so我们上面也说了，要想找到非叶子结点，只需要找下标 i ≤ ⌊n/2⌋ 就可以了，所以这个栗子就是下标从 1~⌊8/2⌋=4 的结点

就这四个结点。

那么我们开始吧！

自底向上调整，先看下标为“4”的结点：

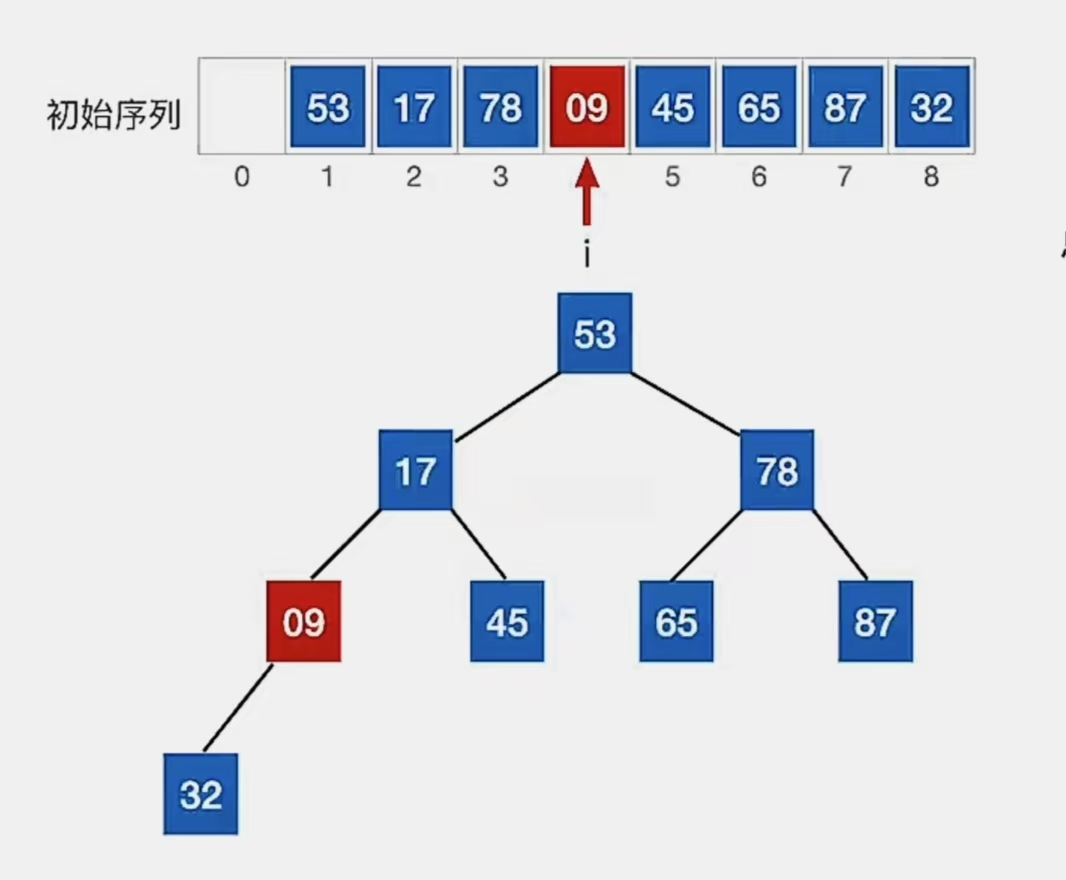
检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“4”的结点“9”不满足我们的要求，所以看它左孩子（2i，下标为“8”）右孩子（2i+1，下标为“9”，超出顺序表长度，所以 i 为“4”时没有右孩子）哪个更大，发现它只有左孩子，所以就和左孩子换：

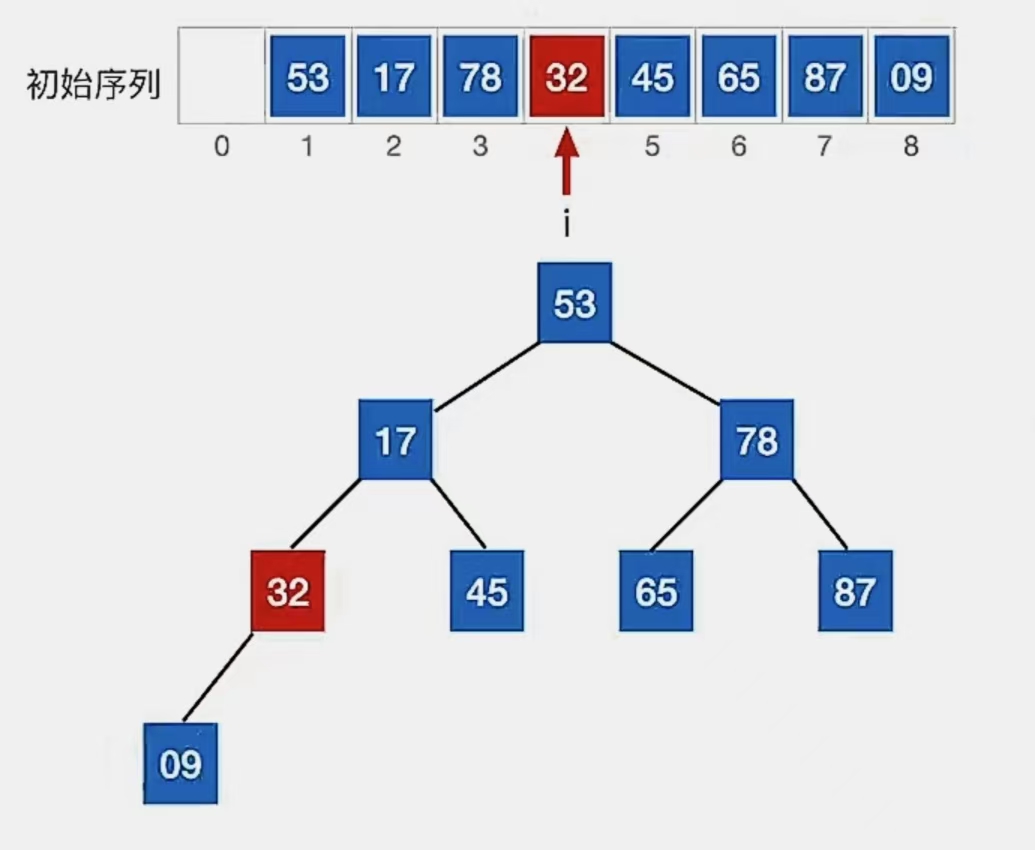
再看下标为“3”的结点：

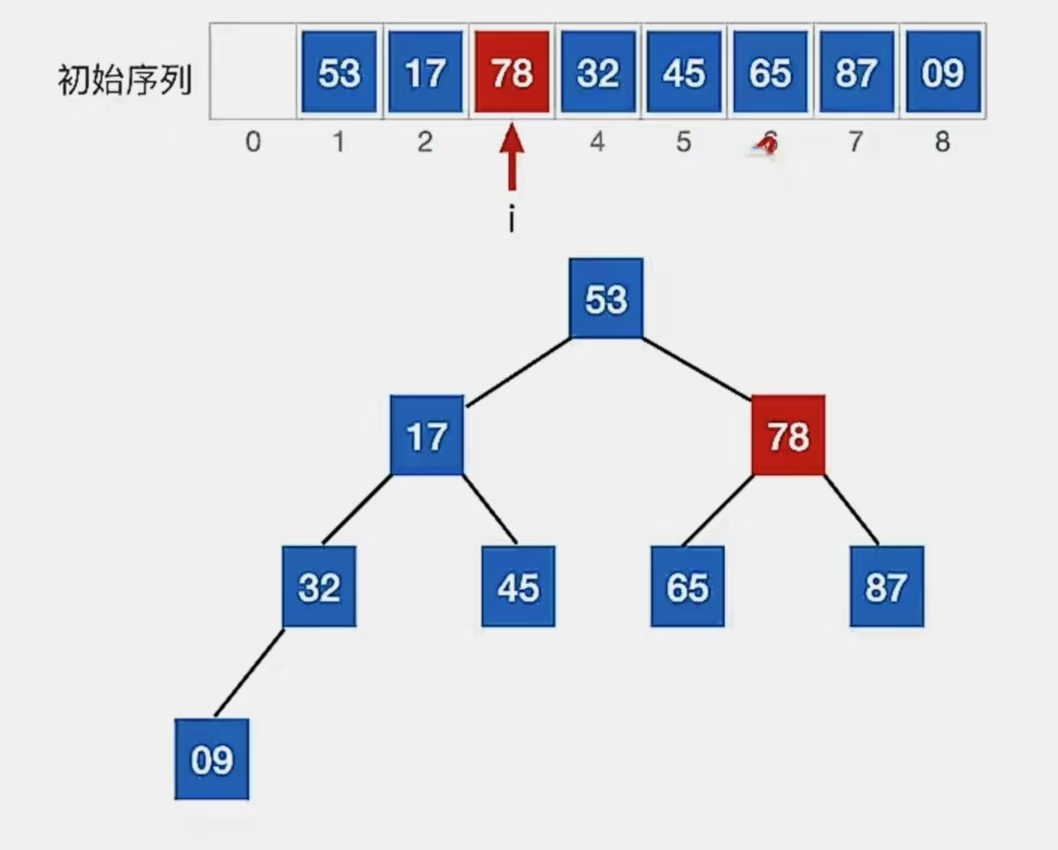
检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“3”的结点“78”不满足我们的要求，所以看它左孩子（2i，下标为“6”，指向元素为“65”）右孩子（2i+1，下标为“7”，指向元素为“87”）哪个更大，发现右孩子更大，所以就和右孩子换：

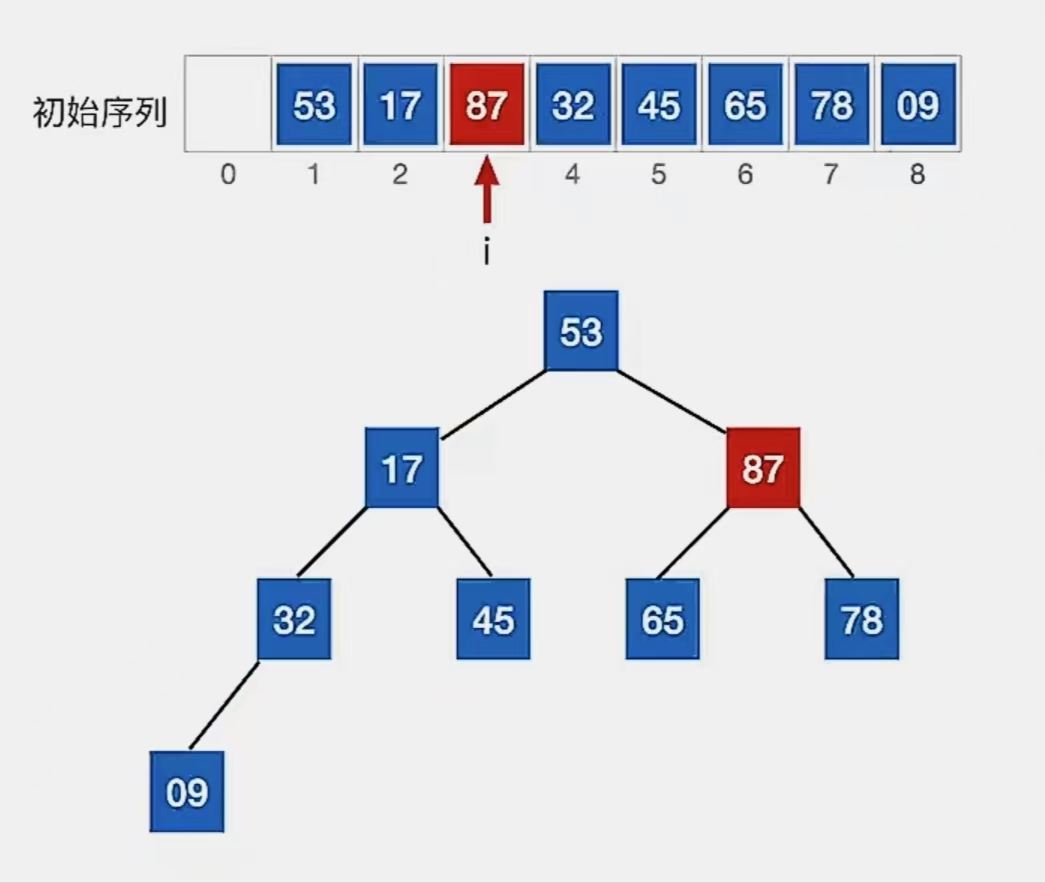
接着看下标为“2”的结点：

检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

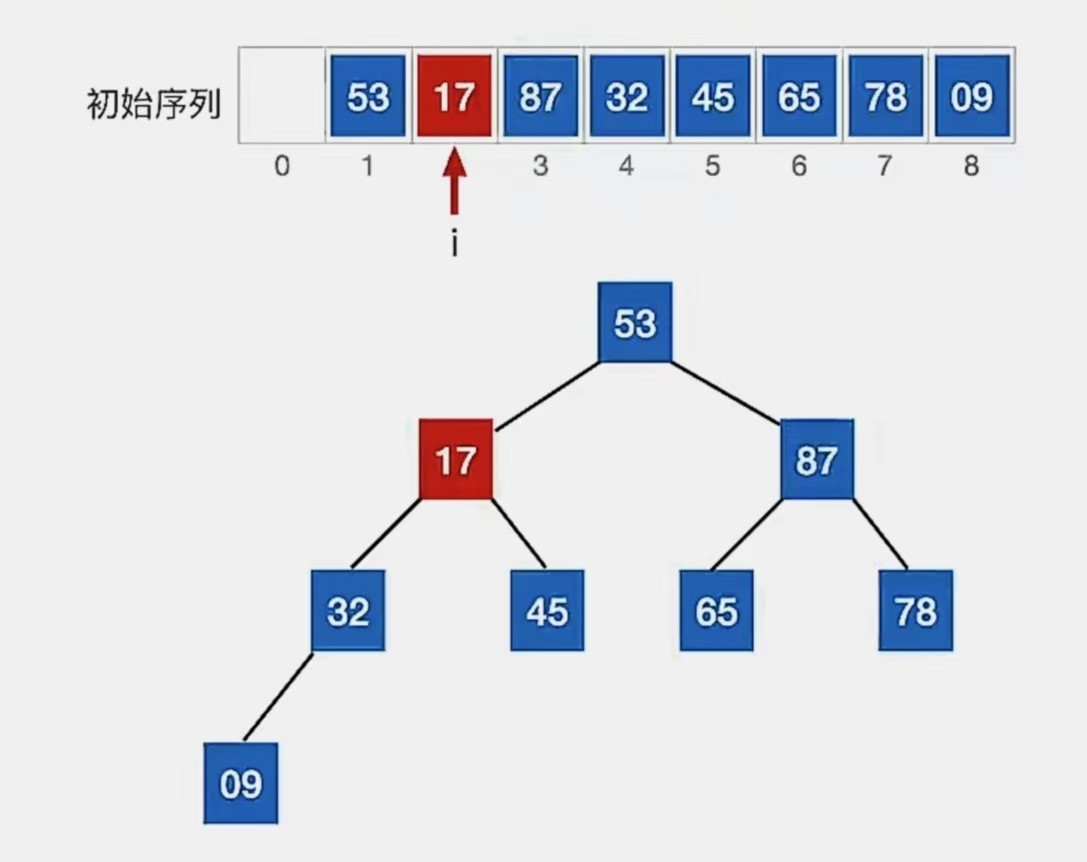
显然下标为“2”的结点“17”不满足我们的要求，所以看它左孩子（2i，下标为“4”，指向元素为“32”）右孩子（2i+1，下标为“5”，指向元素为“45”）哪个更大，发现右孩子更大，所以就和右孩子换：

最后看下标为“1”的结点：

检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

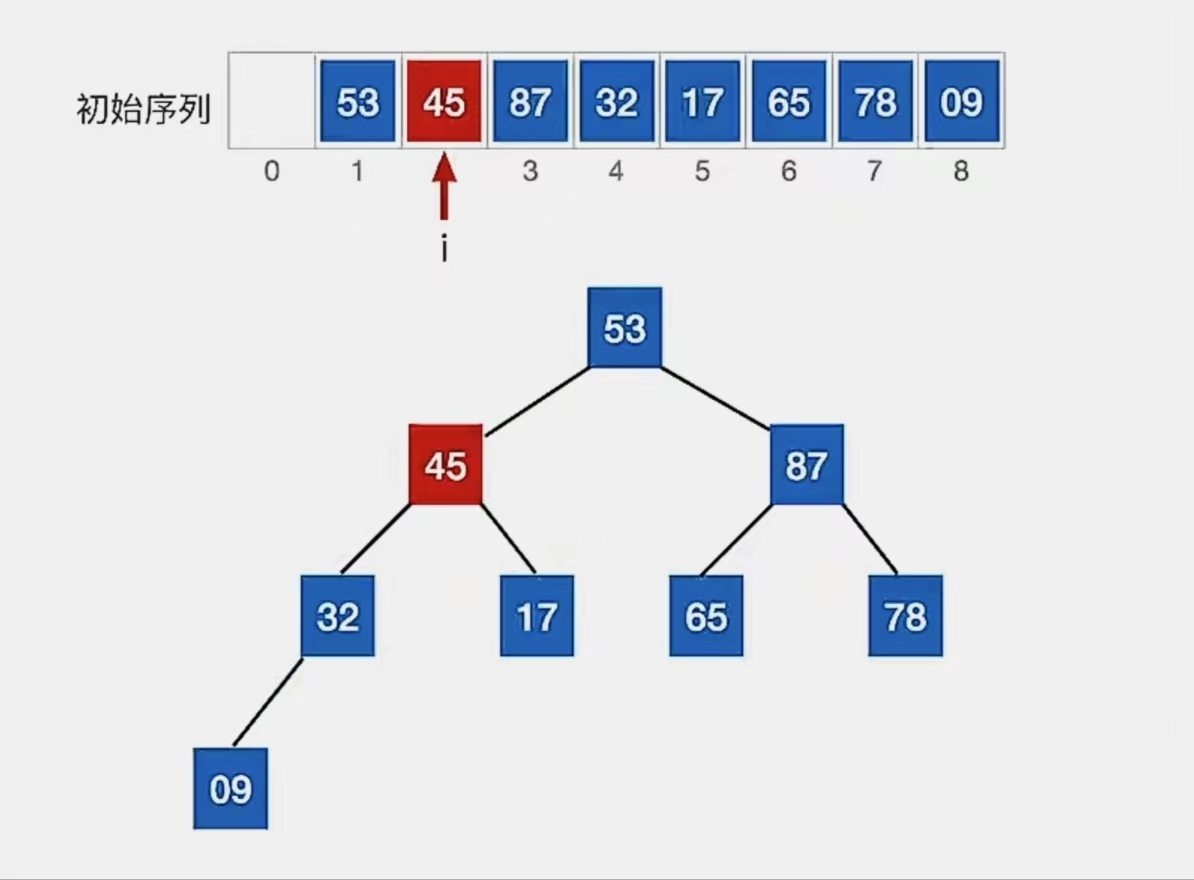
显然下标为“1”的结点“53”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“45”）右孩子（2i+1，下标为“3”，指向元素为“87”）哪个更大，发现右孩子更大，所以就和右孩子换：

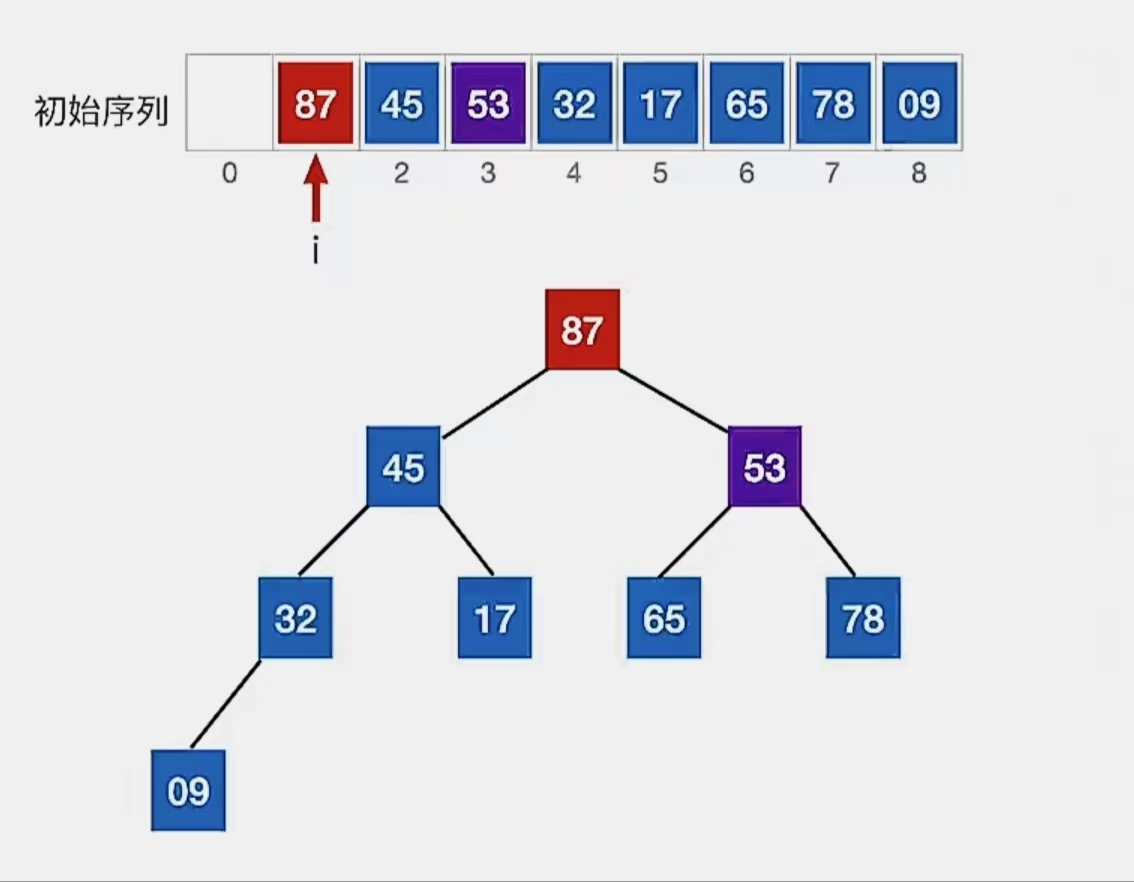
但是！！！！你有没有发现，现在下标为“3”的结点，由于下标为“1”的结点的调整，不满足“大根堆”的要求了！！！

所以我们应该继续调整。

也就是说，如果元素互换破坏了下一级的堆，则采用相同的方法继续往下调整（小元素不断“下坠”）

什么意思呢？我们下标为“1”的结点的右孩子比较大，不是和右孩子换吗

那么换到右孩子这个地方（也就是下标为“3”的地方）之后，还要再以下标为“3”为顶点，继续看它的左右孩子是不是满足大根堆的要求

不满足则继续换，换完之后还要再看看，要么满足大根堆要求了停止，要么没有左右孩子了停止。

so我们还有一波：

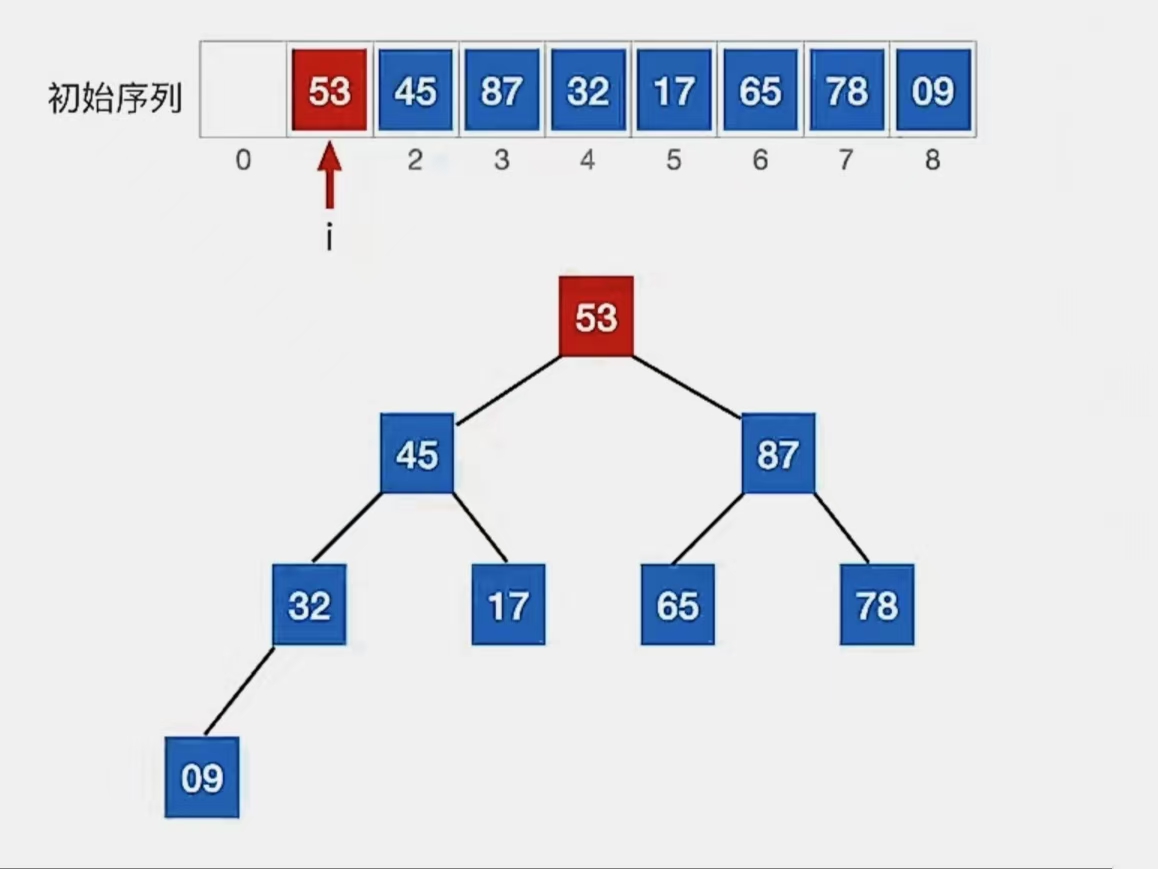
由于破坏了下一级的“堆”，所以看下标为“3”的结点：

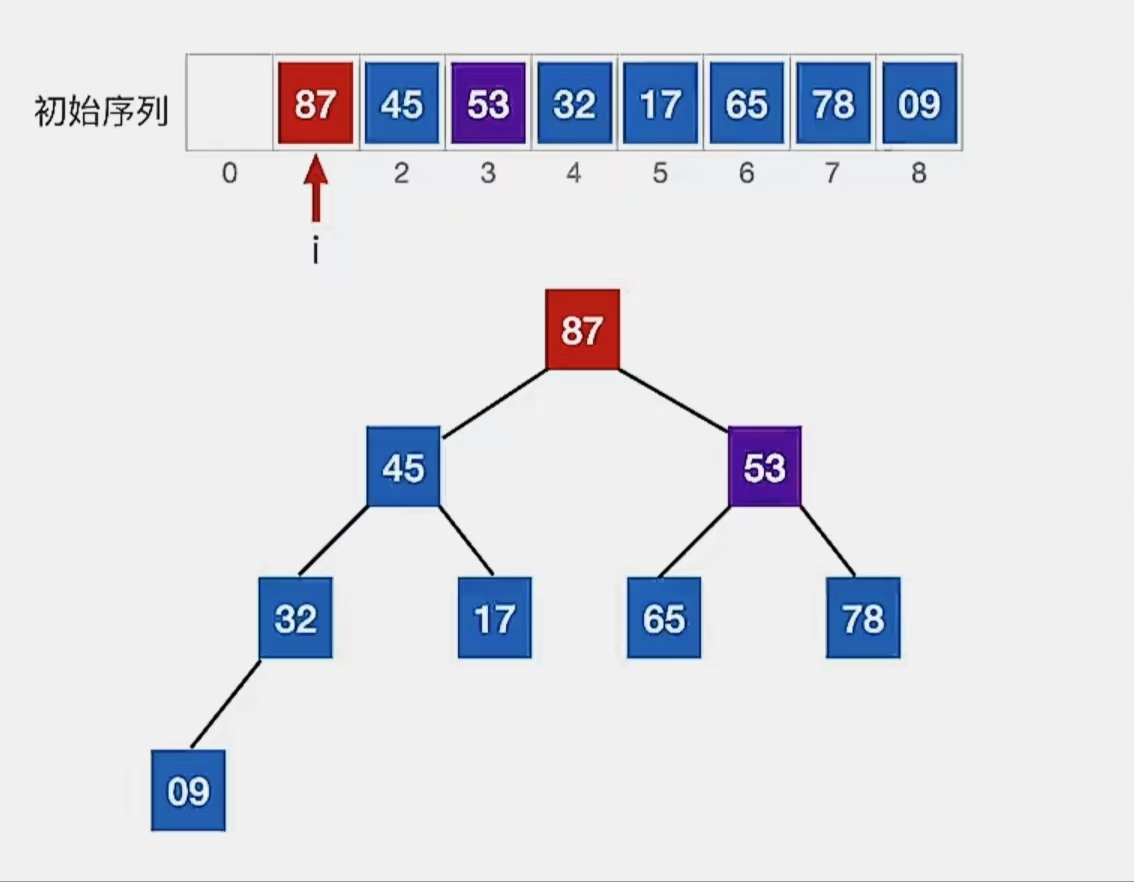
检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“3”的结点“53”不满足我们的要求，所以看它左孩子（2i，下标为“6”，指向元素为“65”）右孩子（2i+1，下标为“7”，指向元素为“78”）哪个更大，发现右孩子更大，所以就和右孩子换：

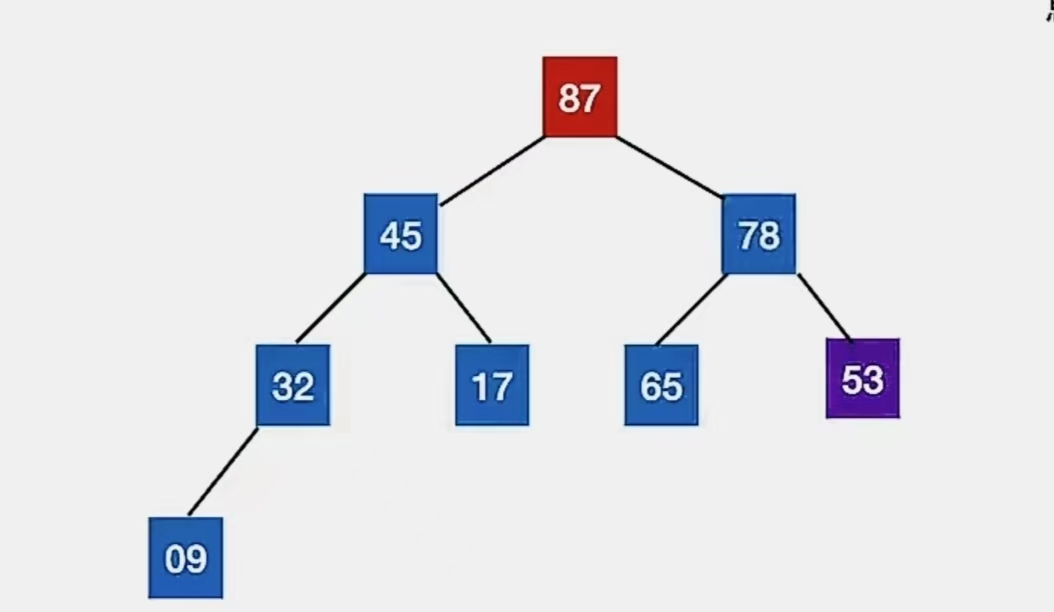
满足大根堆的要求，且小元素（53）无法继续“下坠”，调整完成。

ok，我们上代码：

//将以 k 为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len){A[0] = A[k];                        //A[0]暂存子树的根结点for(int i = 2*k; i<=len; i*=2){     //沿key较大的子结点向下筛选if(i < len && A[i] < A[i+1]){i++;                        //取key较大的子结点的下标}if(A[0] >= A[i]){break;                      //筛选结束}else{              A[k] = A[i];                //将A[i]调整到双亲结点上k = i;                      //修改 k 值，以便继续向下筛选}}A[k] = A[0];                        //被筛选结点的值放入最终位置
}//建立大根堆
void BuildMaxHeap(int A[],int len){//ATTENTION！注意我们这里是从最底层的分支结点开始调整！！！for(int i = len/2; i>0; i--){   //从后往前调整所有非终端结点HeadAdjust(A, i, len);}
}

还是那么清晰。

我们刚刚肉眼看的流程是一眼能看到满不满足大根堆，不满足就调整，但是我们代码一眼看不出来，所以算法是先找出当前结点左右孩子最大的那个，再和根节点比，要是根节点比较大那没事，要是根节点比较小就换。

还有就是上面一个函数是调整一个结点，我们建立“大根堆”，对所有的非叶子结点从后往前都进行一次这样操作即可。

还有我们 A[0] 刚好是空的，所以我们在对一个非叶子结点进行调整的时候，直接让 A[0] 当临时变量即可。

3.堆排序

我们已经会将一个序列调整成一个大根堆了，那么现在就可以根据大根堆进行排序了。

选择排序：每一趟在待排序元素中选取关键字最小（或最大）的元素加入有序子序列。

所以我们堆排序就是：每一趟将堆顶元素加入有序子序列（与待排序序列中的最后一个元素交换），并将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

什么意思呢？就是两步，①堆排序加到有序序列中②调整。

我们还是用之前那个栗子来描述：

这是刚刚那个调整完成的大根堆：

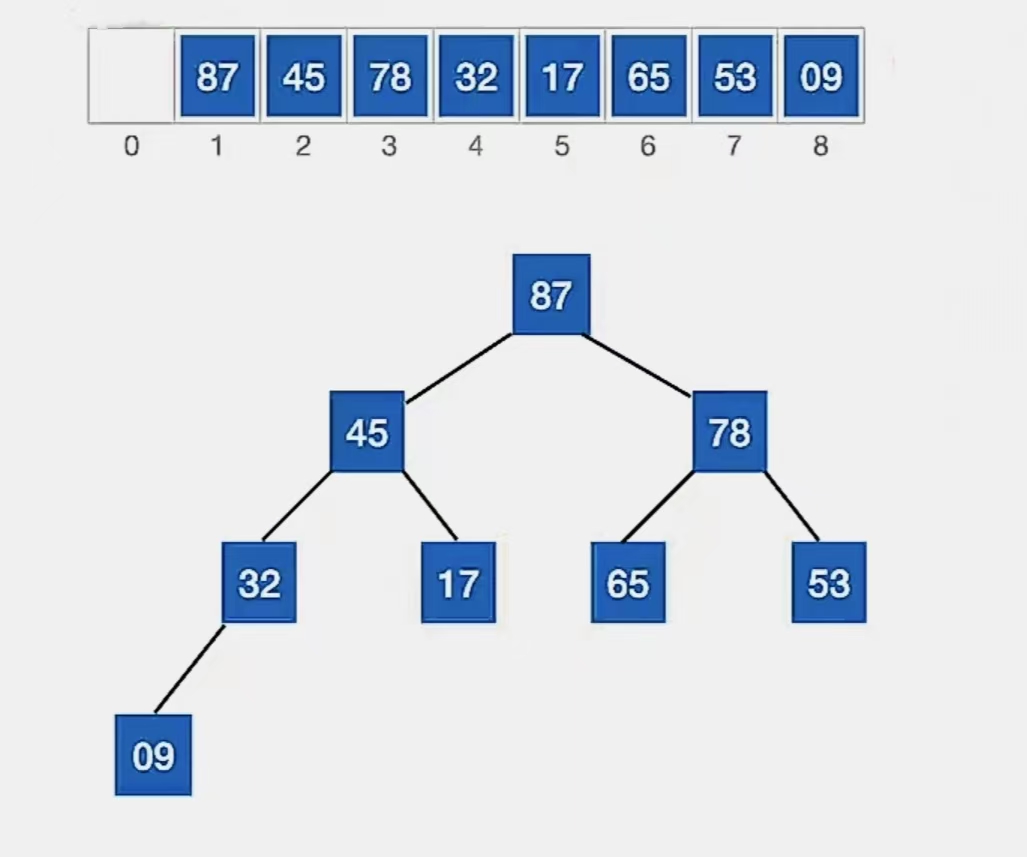
第1趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“87”，将它与待排序元素序列中的最后一个元素（“9”）交换

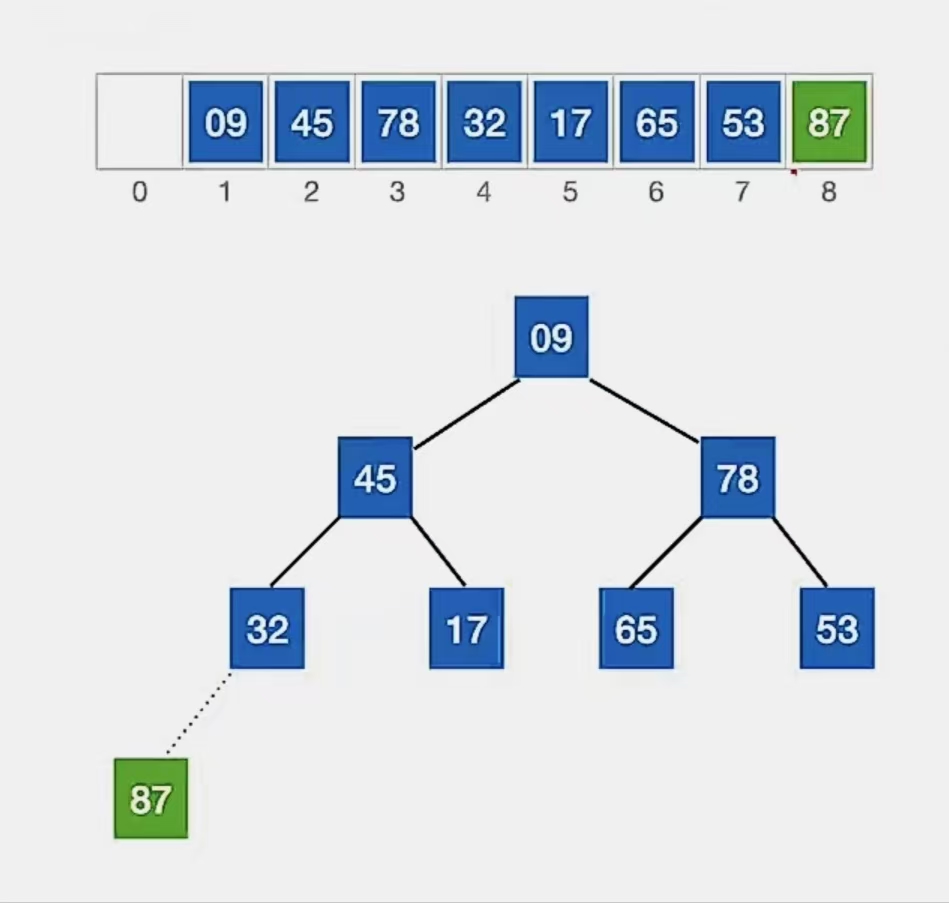
虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~7，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~7 中的自底向上的第一个叶子结点（n为7，第一个非叶子结点下标为 ⌊7/2⌋ = 3）开始调整，发现满足大根堆的要求；再看下标为“2”的结点，也满足大根堆的要求；于是来到了结点“1”，发现不满足：

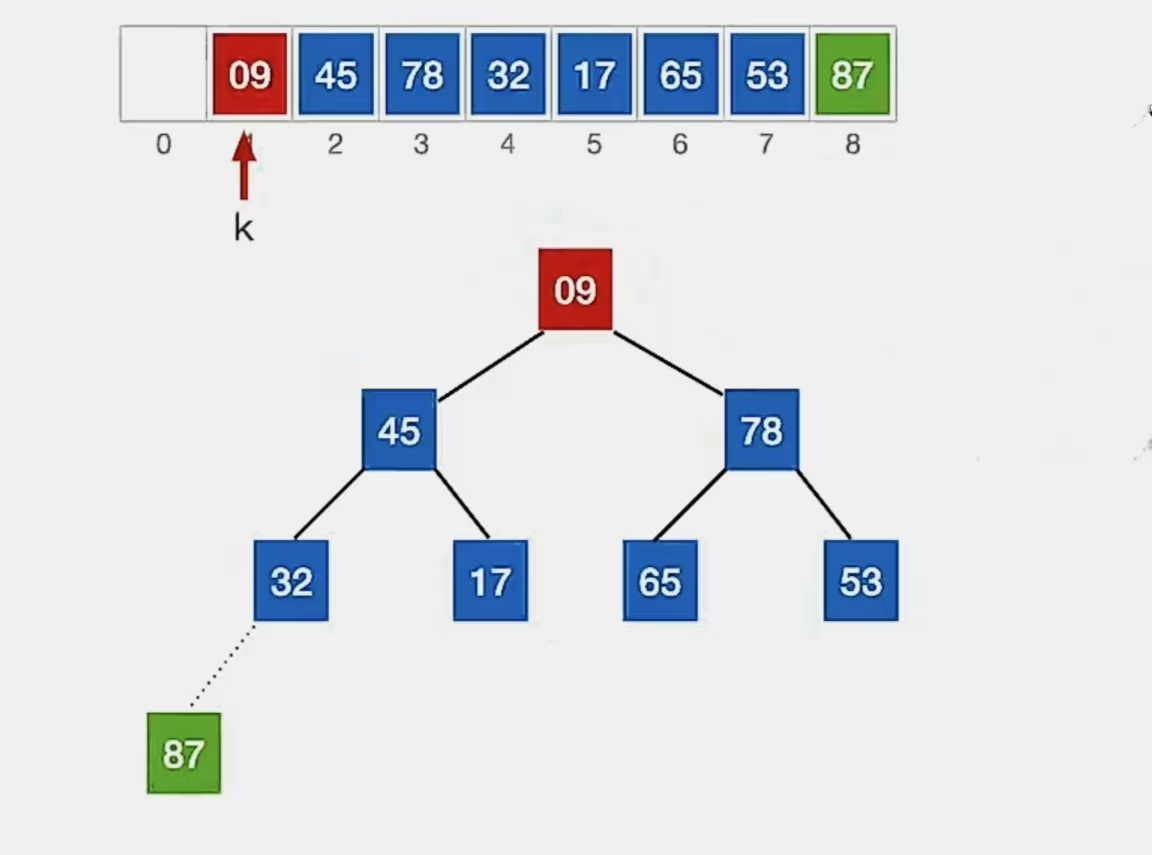
我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“9”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“45”）右孩子（2i+1，下标为“3”，指向元素为“78”）哪个更大，发现右孩子更大，所以就和右孩子换：

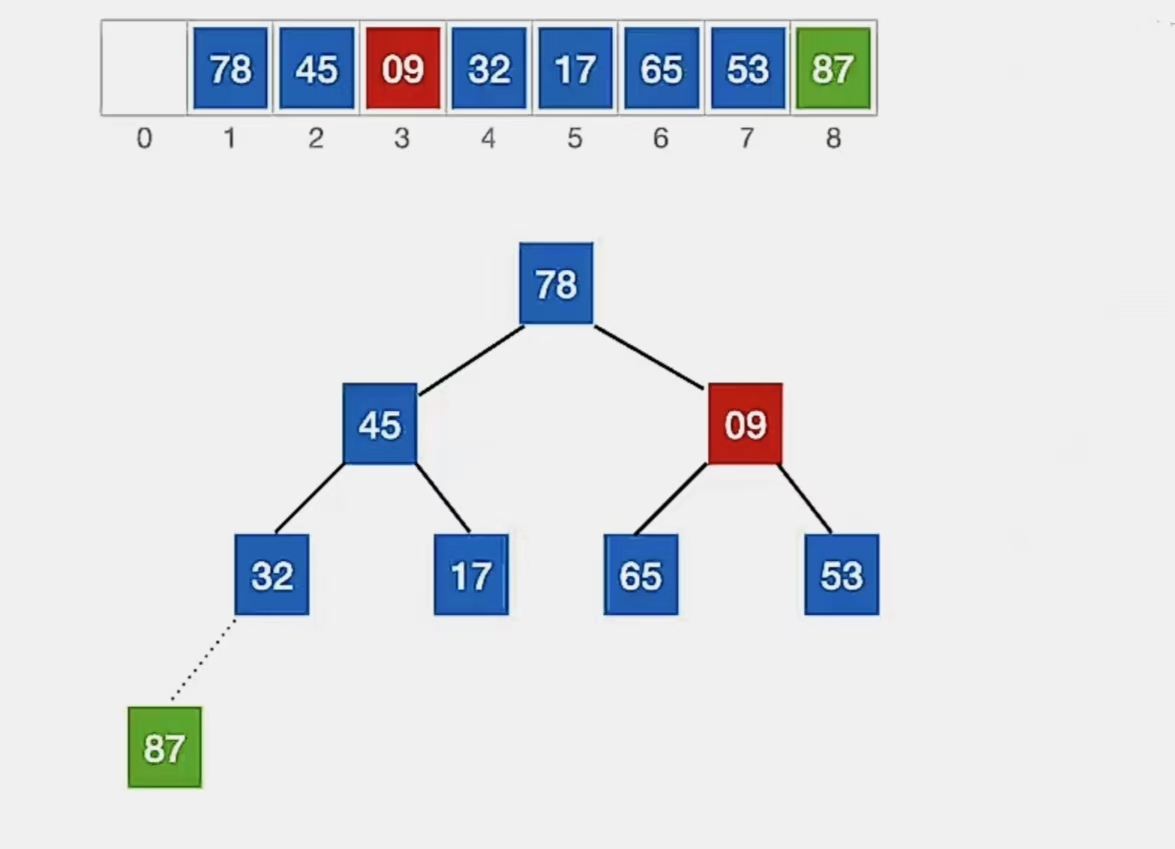
我们再往下看发现它破坏了下一级的堆，所以还要继续向下调整。

换到了下标为“3”这里，那么就开始针对这个下标的结点进行调整：

检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“3”的结点“9”不满足我们的要求，所以看它左孩子（2i，下标为“6”，指向元素为“65”）右孩子（2i+1，下标为“7”，指向元素为“53”）哪个更大，发现左孩子更大，所以就和左孩子换：

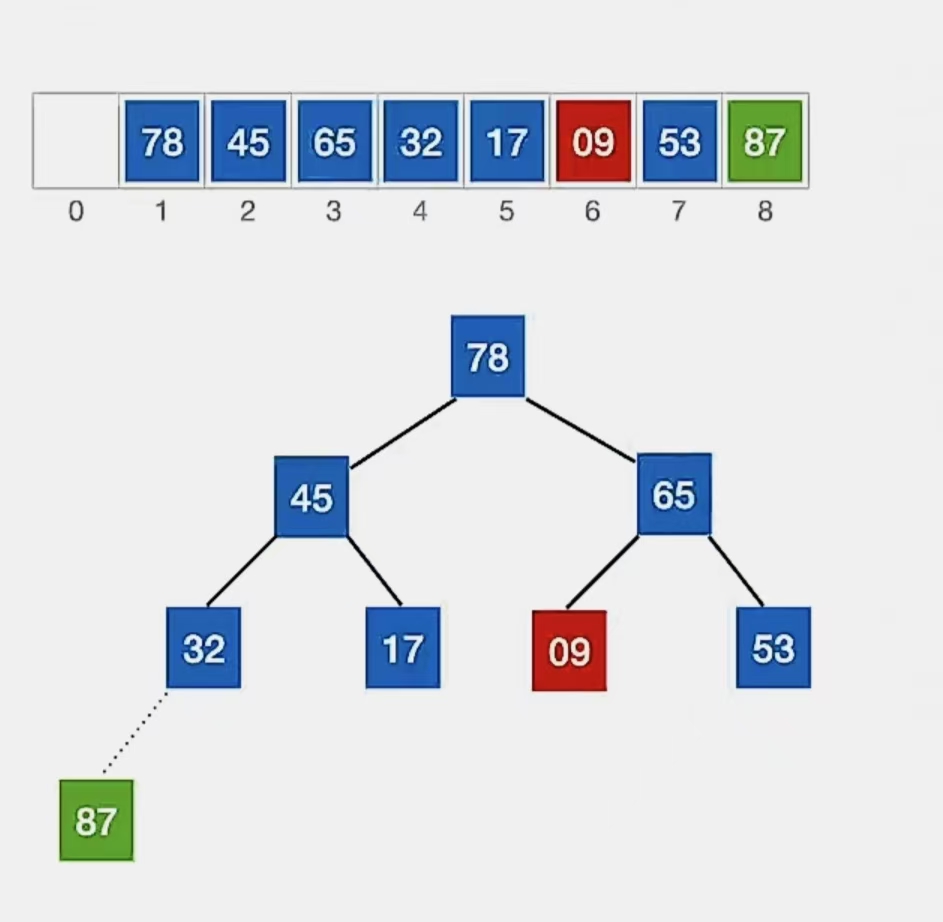
换完发现没有孩子了，小元素无法下坠，所以调整完成。

那么我们第1趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第2趟堆排序了：

第2趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“78”，将它与待排序元素序列中的最后一个元素（“53”）交换

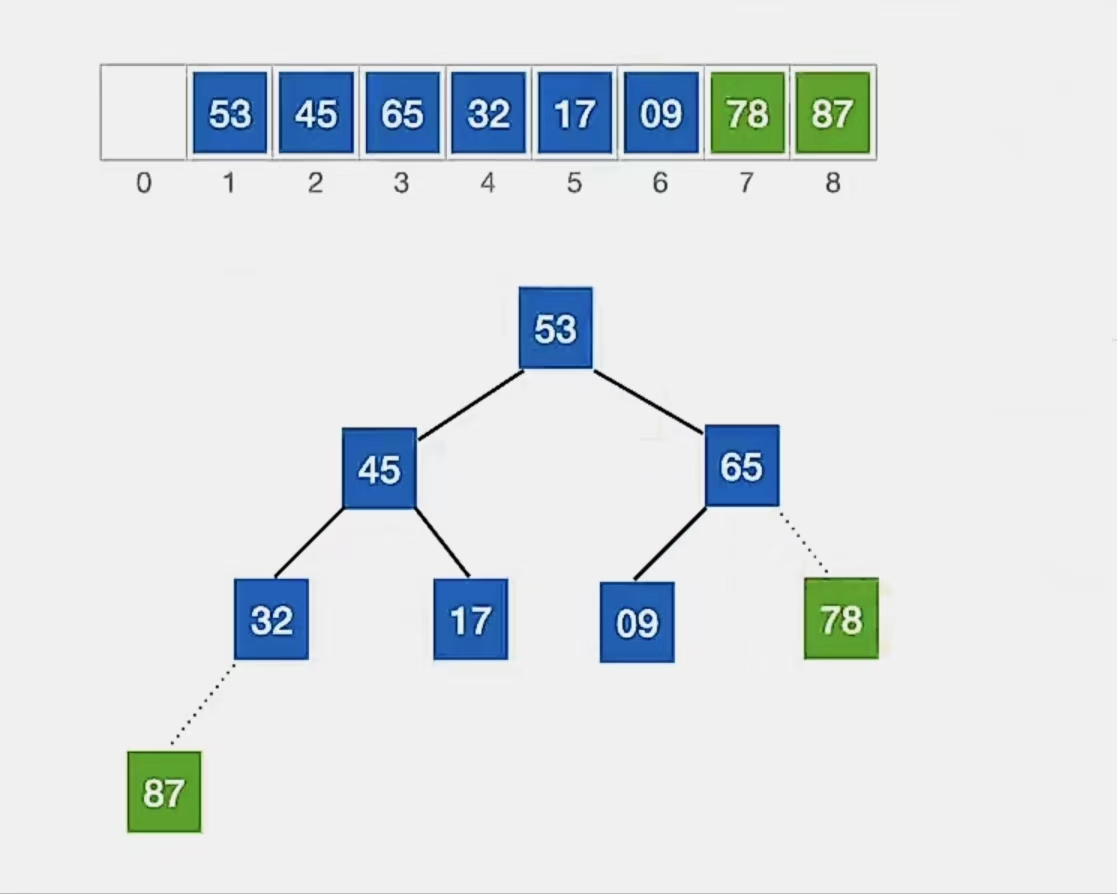
虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~6，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~6 中的自底向上的第一个叶子结点（n为6，第一个非叶子结点下标为 ⌊6/2⌋ = 3）开始调整，发现满足大根堆的要求；再看下标为“2”的结点，也满足大根堆的要求；于是来到了结点“1”，发现不满足：

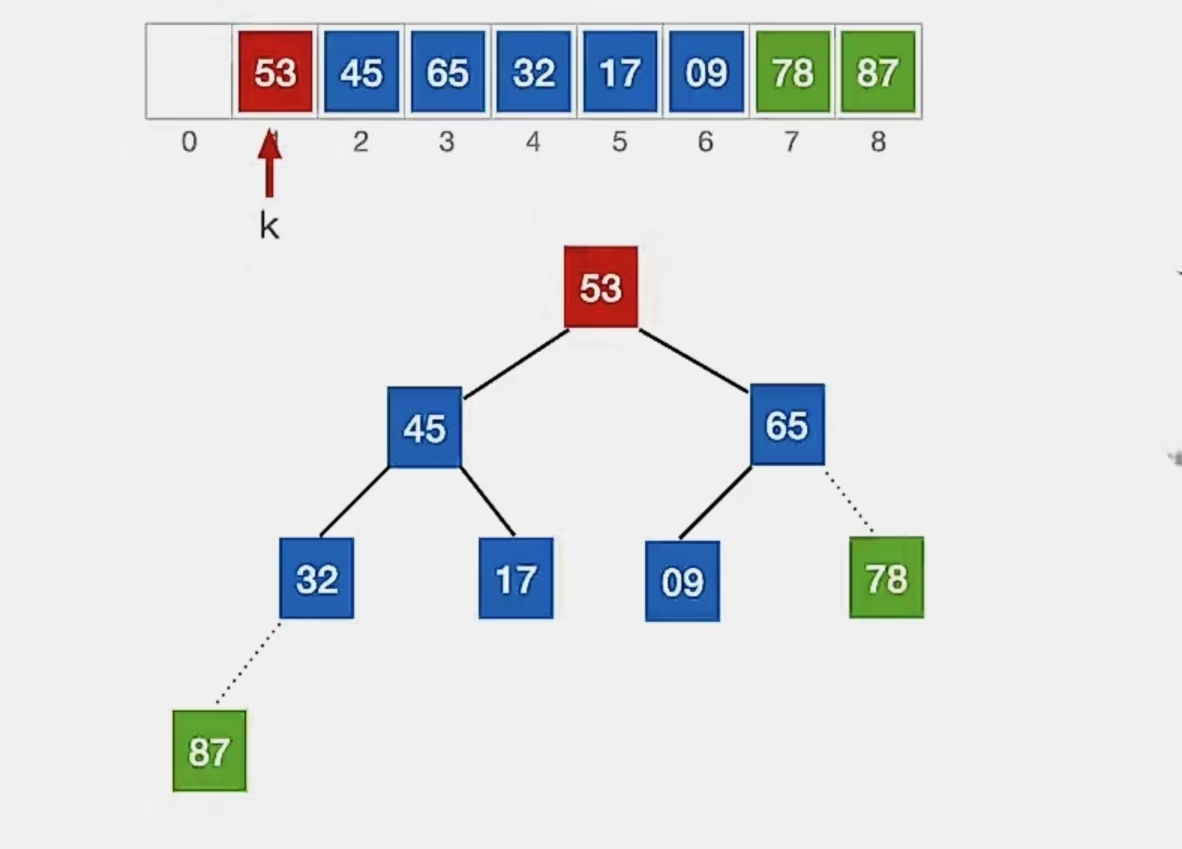
我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“53”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“45”）右孩子（2i+1，下标为“3”，指向元素为“65”）哪个更大，发现右孩子更大，所以就和右孩子换：

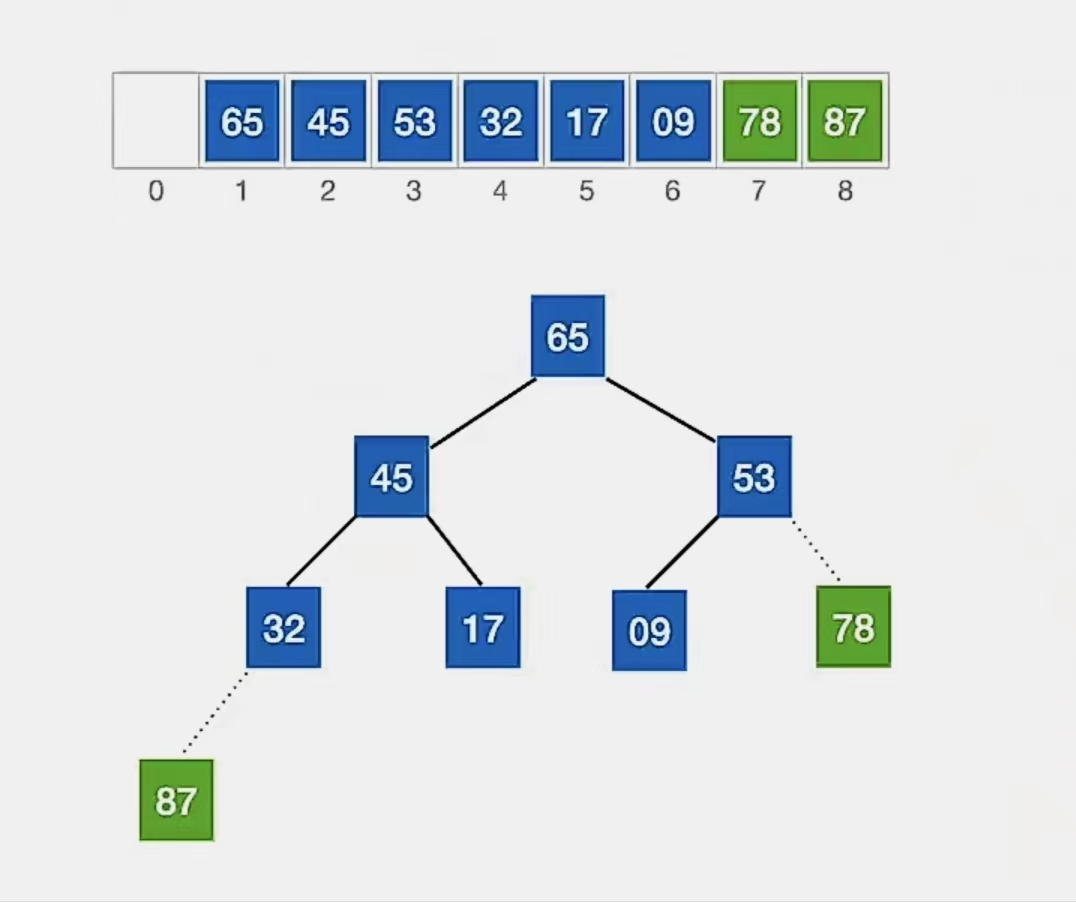
换完发现左孩子比它小，小元素无法下坠，所以调整完成。

那么我们第2趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第3趟堆排序了：

第3趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“65”，将它与待排序元素序列中的最后一个元素（“9”）交换：

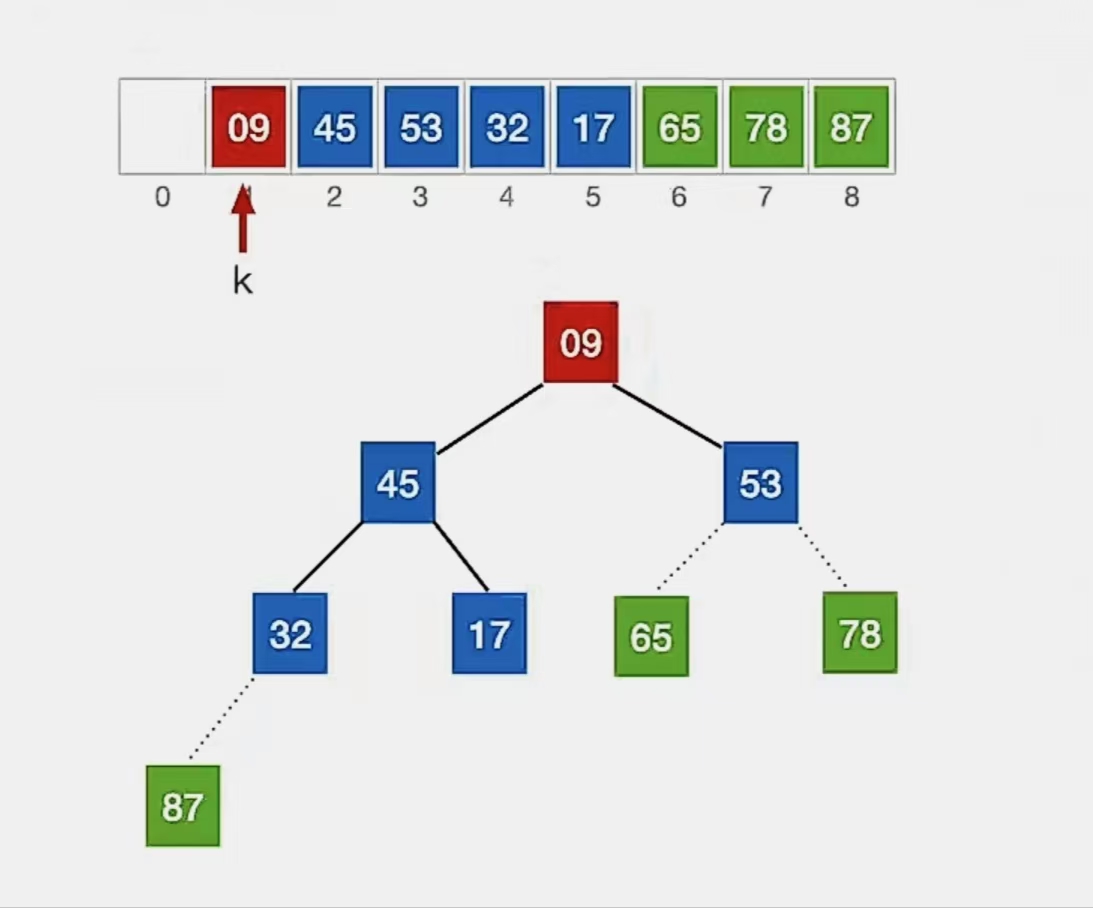
虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~5，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~5 中的自底向上的第一个叶子结点（n为5，第一个非叶子结点下标为 ⌊5/2⌋ = 2）开始调整，发现满足大根堆的要求；于是来到了结点“1”，发现不满足：

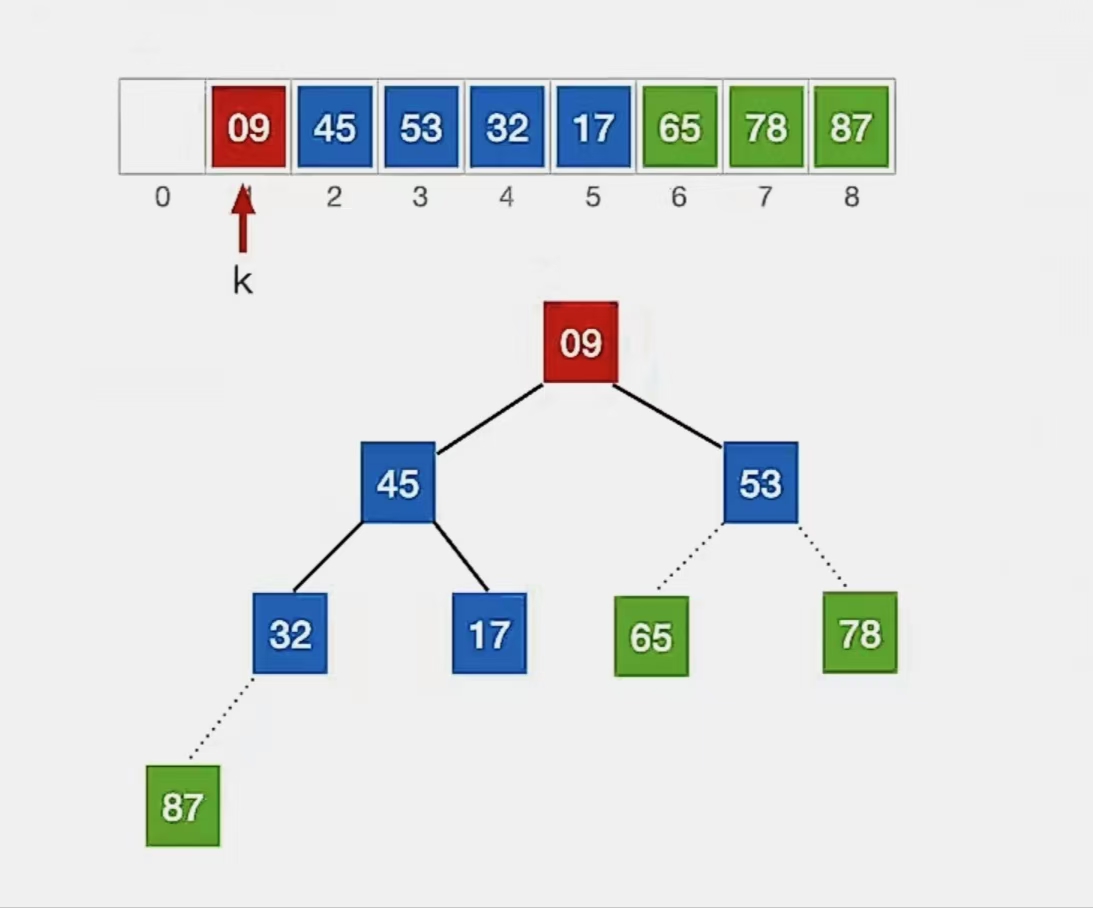
我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“9”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“45”）右孩子（2i+1，下标为“3”，指向元素为“53”）哪个更大，发现右孩子更大，所以就和右孩子换：

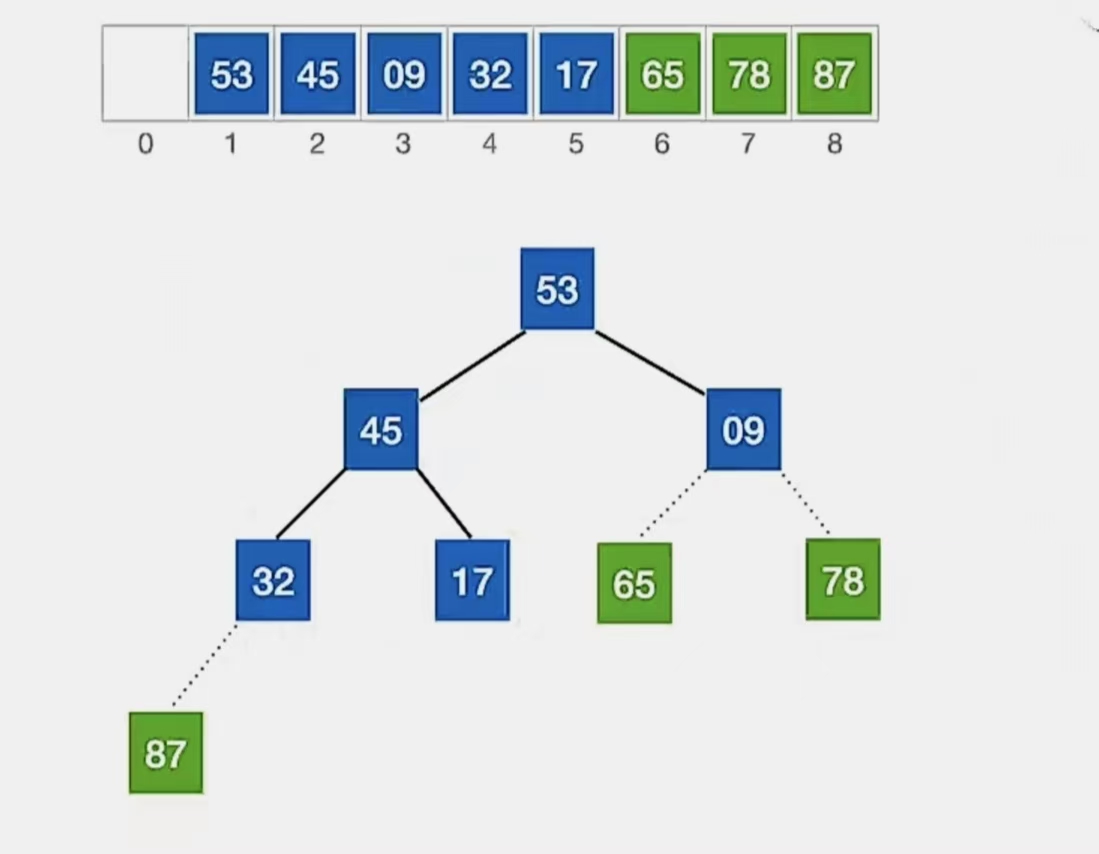
换完发现左孩子比它小，小元素无法下坠，所以调整完成。（虚线是已排好序的不用管，别弄混了）

那么我们第3趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第4趟堆排序了：

第4趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“53”，将它与待排序元素序列中的最后一个元素（“17”）交换：

虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~4，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~4 中的自底向上的第一个叶子结点（n为4，第一个非叶子结点下标为 ⌊4/2⌋ = 2）开始调整，发现满足大根堆的要求；于是来到了结点“1”，发现不满足：

我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“17”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“45”）右孩子（2i+1，下标为“3”，指向元素为“9”）哪个更大，发现左孩子更大，所以就和左孩子换：

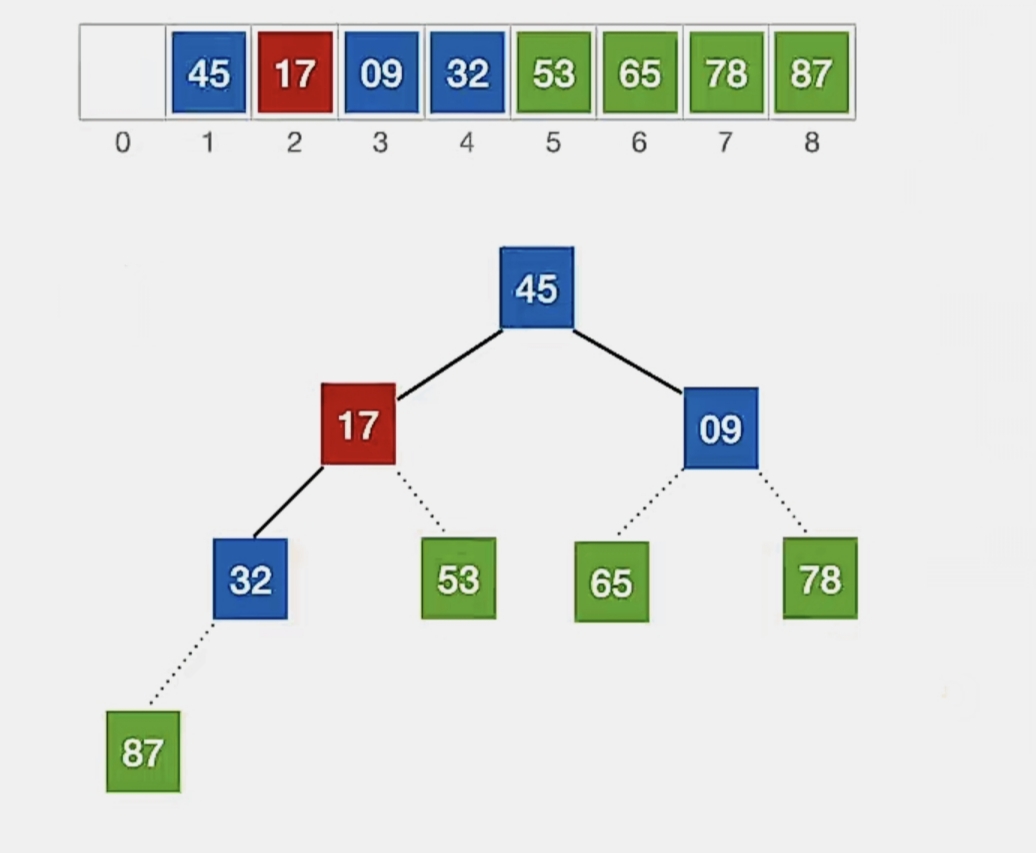
我们再往下看发现它破坏了下一级的堆，所以还要继续向下调整。

换到了下标为“2”这里，那么就开始针对这个下标的结点进行调整：

检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“2”的结点“17”不满足我们的要求，所以看它左孩子（2i，下标为“4”，指向元素为“32”）右孩子（2i+1，下标为“5”，超出待排序顺序表长度，所以 i 为“4”时待排序元素中没有右孩子）哪个更大，发现左孩子更大，所以就和左孩子换：

换完发现没有孩子了，小元素无法下坠，所以调整完成。

那么我们第4趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第5趟堆排序了：

第5趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“45”，将它与待排序元素序列中的最后一个元素（“17”）交换：

虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~3，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~3 中的自底向上的第一个叶子结点（n为3，第一个非叶子结点下标为 ⌊3/2⌋ = 1）开始调整，发现不满足大根堆的要求：

我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“17”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“32”）右孩子（2i+1，下标为“3”，指向元素为“9”）哪个更大，发现左孩子更大，所以就和左孩子换：

换完发现没有孩子了，小元素无法下坠，所以调整完成。

那么我们第5趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第6趟堆排序了：

第6趟堆排序

堆排序：①将堆顶元素加入有序子序列（与待排序元素序列中的最后一个元素交换），②将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

①堆顶元素是“32”，将它与待排序元素序列中的最后一个元素（“9”）交换：

虚线表示已经加入有序序列，我们就不用管它了。

②现在待排序元素是下标 1~2，我们将它调整为大根堆

还是按照上面的方式，从 下标 1~2 中的自底向上的第一个叶子结点（n为2，第一个非叶子结点下标为 ⌊2/2⌋ = 1）开始调整，发现不满足大根堆的要求：

我们开始调整，检查当前结点是否满足 根≥左、右，若不满足，将当前结点与更大的一个孩子互换。

显然下标为“1”的结点“9”不满足我们的要求，所以看它左孩子（2i，下标为“2”，指向元素为“17”）右孩子（2i+1，下标为“3”，超出待排序顺序表长度，所以 i 为“3”时待排序元素中没有右孩子）哪个更大，发现左孩子更大，所以就和左孩子换：

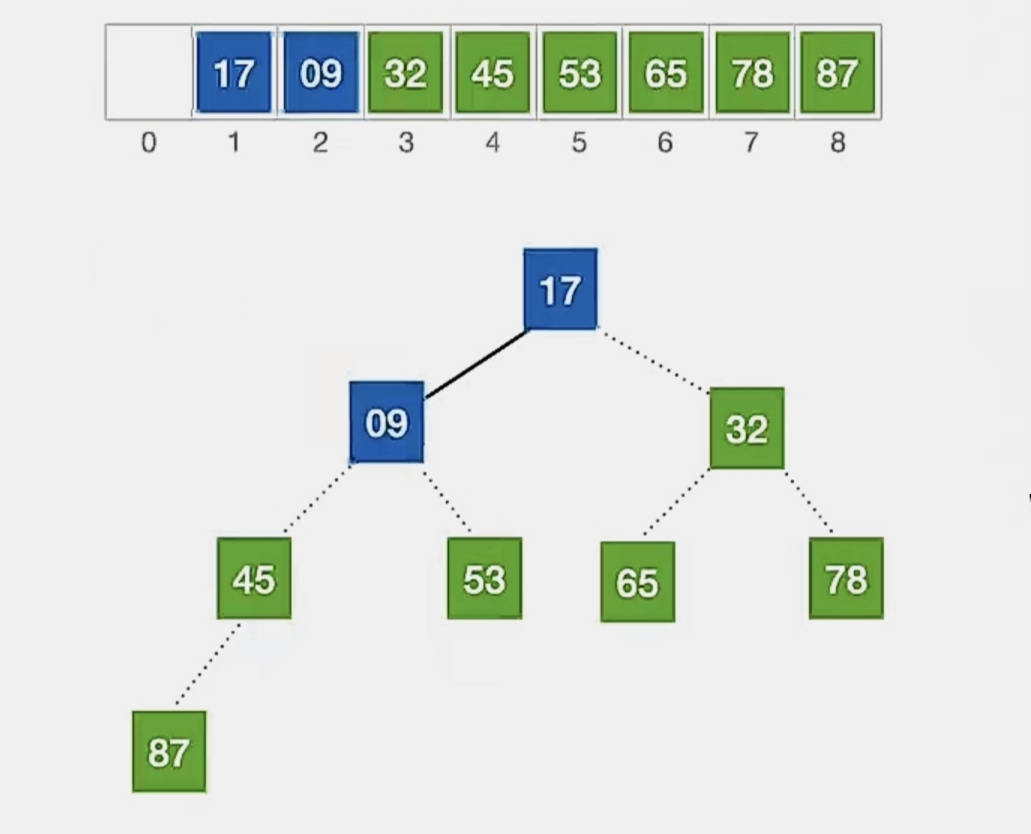
换完发现没有孩子了，小元素无法下坠，所以调整完成。

那么我们第6趟也完成了，经过调整后带排序序列再次构成一个“大根堆”，就可以进行第7趟堆排序了：

第7趟堆排序

我们现在待排序序列只剩下一个元素了，只剩一个元素就不用再调整了：

所以我们一共有 8 个元素，经过 n-1 （7）趟排序后，得到了一个有序的序列：

注意：基于“大根堆”的堆排序得到“递增序列”

操作流程讲完了，我们话不多说，上代码：

//堆排序的完整逻辑
void HeapSort(int A[],int len){BuildMaxHeap(A, len);       //初始建堆for(int i = len; i>1; i--){ // n-1 趟的交换和建堆过程swap(A[i], A[1]);       //堆顶元素和堆底元素交换HeadAdjust(A, 1, i-1);  //把剩余的待排序元素整理成堆}
}//将以 k 为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len){A[0] = A[k];                        //A[0]暂存子树的根结点for(int i = 2*k; i<=len; i*=2){     //沿key较大的子结点向下筛选if(i < len && A[i] < A[i+1]){i++;                        //取key较大的子结点的下标}if(A[0] >= A[i]){break;                      //筛选结束}else{              A[k] = A[i];                //将A[i]调整到双亲结点上k = i;                      //修改 k 值，以便继续向下筛选}}A[k] = A[0];                        //被筛选结点的值放入最终位置
}//建立大根堆
void BuildMaxHeap(int A[],int len){for(int i = len/2; i>0; i--){   //从后往前调整所有非终端结点HeadAdjust(A, i, len);}
}

可以看到堆排序其实就是两步，一个交换，一个下坠。

交换 是每一趟将堆顶元素加入有序子序列（待排序序列中的最后一个元素交换）

下坠 是将待排序元素序列再次调整为大根堆（小元素不断“下坠”）

在堆排序代码中，指针 i 指向的是待排序序列中的最后一个（堆底元素），每进行一趟待排序序列就会少一个。

4.性能

空间复杂度不用说了，显然是O(1)。

废话多预警！！！只要知道结论即可，我下面说的有点细了可不看。

由上面的代码可以看到，我们堆排序主要调用了两个函数，一个是建立大根堆（建堆也是一个接一个调整成堆），一个是遍历待排序元素每一个遍历把all待排序序列调整成堆，这没毛病吧。

而我们被调用的“将以 k 为根的子树调整为大根堆”的函数中，其实针对每一个被调整的结点“k”，都要看它的孩子是不是满足“大根堆”的要求。

怎么看，就是先把它的左右孩子作对比，看哪个大，再把该结点和左右孩子最大的那个作对比，看哪个大，该结点大则不用下坠，该结点小则下坠一层。

so 显然，我们一个结点，每“下坠”一层，最多只需要对比关键字2次，这也没毛病吧。

所以，如果树高为 h ，某结点在第 i 层，那么将这个结点向下调整最多只需要“下坠” h-i 层，关键字对比次数不超过 2(h-i) 次

因为最多就下降到底嘛，再多也没了是吧。

我们又知道 n 个结点的完全二叉树树高 h = ⌊log₂n⌋ + 1 ，所以 n 个结点的树，某结点在第 i 层，那么将这个结点向下调整最多只需要“下坠” h-i 即 ⌊log₂n⌋ + 1 - i 层，关键字对比次数不超过 2(h-i) 即 2（⌊log₂n⌋ + 1 - i） 次

而第 i 层最多有 2^i-1 个结点，这个我们是知道的吧。那最后一层的结点肯定是无法下坠的，因为已经在最底层了，所以只有第 1~(h-1) 层的结点才有可能需要“下坠”调整

so 将整棵树调整为大根堆，关键字对比次数不超过 1 * 2（h-1）+ 2¹ * 2(h-2) + …… + 2^h-2 * 2 次

啥意思呢，就是刚刚说的列了个式子，第 1 层 1 个结点，每个结点最多下坠 h-1 层，每次下坠最多对比关键字2次，所以第 1 层最多对比 1 * 2（h-1） 次；第 2 层 2 个结点，每个结点最多下坠 h-2 层，每次下坠最多对比关键字2次，所以第 2 层最多对比 2¹ * 2(h-2) 次……以此类推，第 h-1 层 有 2^h-2 个结点，每个结点最多下坠 1 层，每次下坠最多对比关键字2次，所以第 h-1 层最多对比 2^h-2 * 2 次

所以将整棵树调整为大根堆，关键字对比次数不超过 1 * 2（h-1）+ 2¹ * 2(h-2) + …… + 2^h-2 * 2 次

然后把 h = ⌊log₂n⌋ + 1 代入进去，再经过一些数学运算，什么基本不等式之类的，再来一点差比数列求和，再来个错位相减法啥的……最终可以得到这个加和 ≤ 4n（感兴趣的可以自己查一下哈，计算机的尽头是数学……）

所以！！！我们建堆的过程，关键字对比次数不超过 4n，建堆时间复杂度 = O(n)

建堆时间复杂度其实就是将整棵树调整为堆的时间复杂度，没差。

而我们堆排序算法中，首先调用建堆是吧，但建堆之后还有呢，建堆之后需要进行 n-1 趟，每一趟交换后都需要将根节点进行“下坠”调整。（弱弱说一句，注意这里不是将整棵树调整成堆了，是只将根结点调整成堆，只调整根结点一个结点）

根结点最多下坠 h-1 层，每次下坠最多对比关键字 2 次，所以每一趟排序时间复杂度不超过 O(h)=O(log₂n)

刚刚又说了建堆之后需要进行 n-1 趟，总的时间复杂度就是O(nlog₂n)

所以我们完整堆排序的时间复杂度就是 O(n) + O(nlog₂n) = O(nlog₂n)

那么稳定性如何？

假设我们有一个初始序列，那要进行堆排序，我们首先要做的就是把它初始化为大根堆：

由我们的 “将以 k 为根的子树调整为大根堆” 代码可以看到，若左右孩子一样大，则我们的规则是优先和左孩子进行交换的。

so 调整后就变成这样：

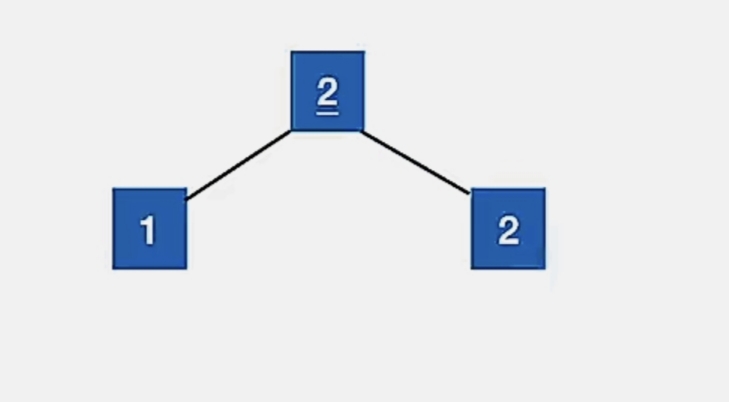
我们的大根堆就建立完成了。

大根堆建立完成后我们就可以进行堆排序了。先把堆顶元素加入到有序子序列：

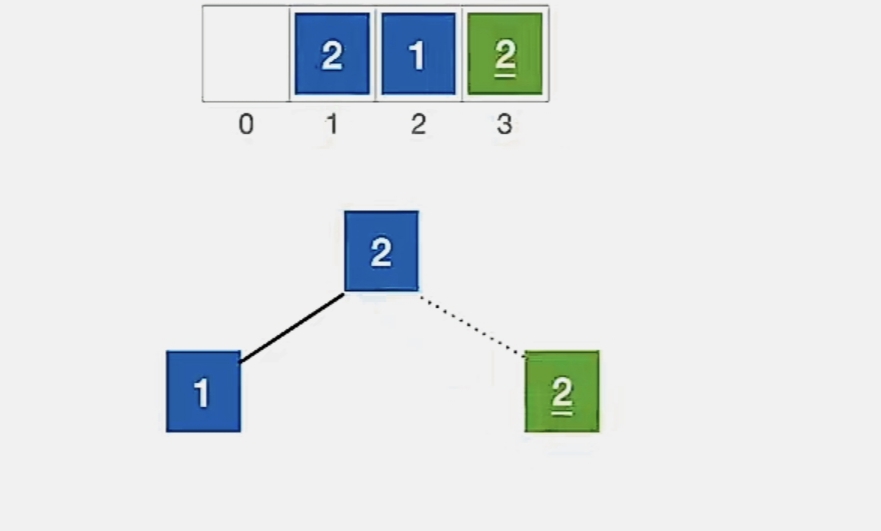
发现待排序序列还是满足大根堆。再把堆顶元素加入有序子序列：

现在待排序序列就剩一个元素了，排序完成了：

我们发现一样的元素调换位置了，所以堆排序是不稳定的。

当然，我们上面说的堆排序都是大根堆，得到的是递增序列，那么基于小根堆的堆排序得到的就是递减序列了，其实过程都是一样的，不再赘述。

三、堆的插入和删除

1.插入

先提前说一下，我们插入一个元素都是放在表尾。

对于小根堆，新元素放到表尾，与新元素的双亲结点对比，若新元素比双亲结点更小，则将二者互换。新元素就这样一路“上升”，直到无法继续上升为止。

显然堆的插入其实主要操作还是调整堆。

我们来看，这是一个平平无奇水灵灵的小根堆：

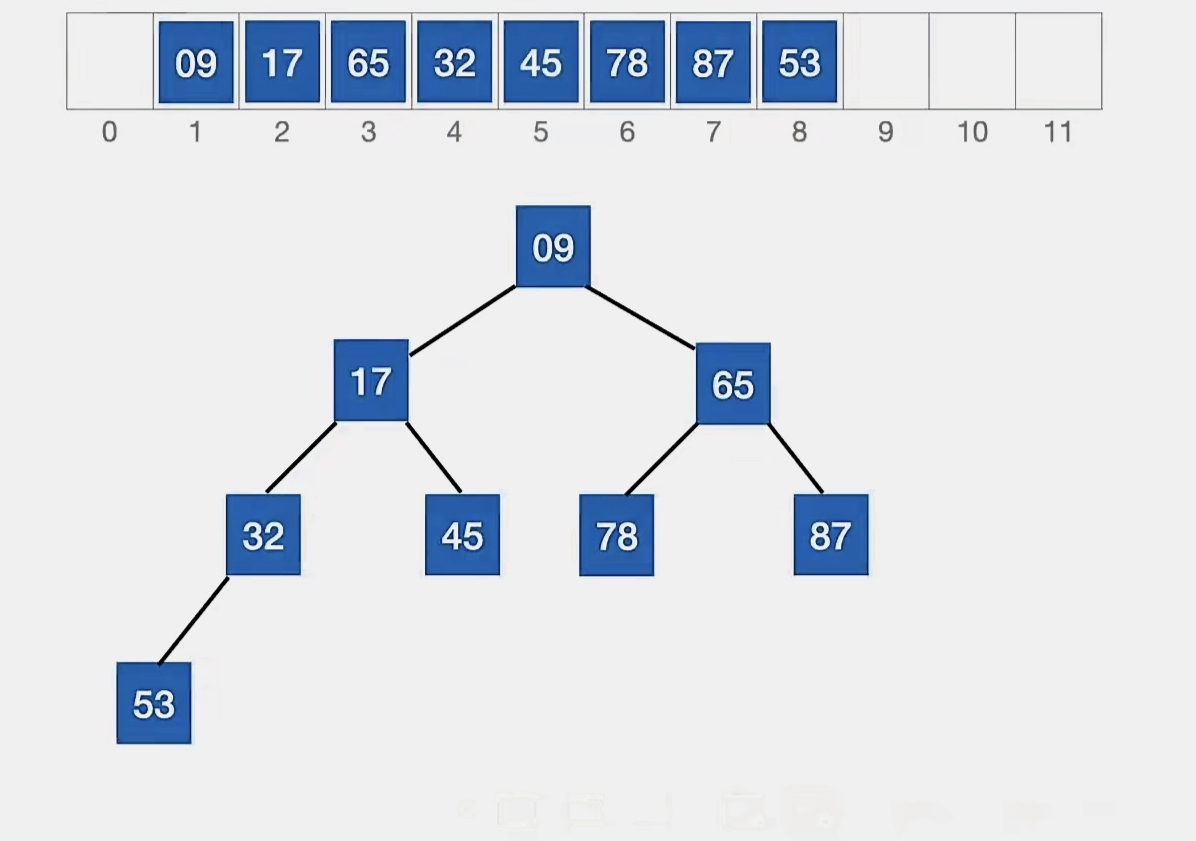
现在我们要往这个堆里面插入元素“13”

新元素放到表尾，所以放到末尾：

此时我们应该调整“堆”，把新元素与它的的双亲结点对比，若新元素比双亲结点更小，则将二者互换。新元素就这样一路“上升”，直到无法继续上升为止。

13<32，所以我们调换：

13<17，所以我们再调换：

此时 13>9，无法再“上升”了，这就是它的最终位置。

我们对比关键字的次数是 3 次。

现在我们要往这个堆里面插入元素“46”

新元素放到表尾，所以放到末尾：

此时我们应该调整“堆”，把新元素与它的的双亲结点对比，若新元素比双亲结点更小，则将二者互换。新元素就这样一路“上升”，直到无法继续上升为止。

46>45，无法再“上升”，这就是它的最终位置，我们不用换：

对比关键字的次数只有 1 次。

好了，堆的插入就说完了，现在我们来说堆的删除：

2.删除

我们在堆里面删除元素，被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止。

这是我们刚刚插入新元素调整后的小根堆：

现在我们要在这个堆中删除元素“13”

被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止。

所以我们用“46”来代替被删元素：

45>17，46>17，所以我们调换“46”和“17”：

53>32，46>32，所以我们再调换：

此时元素“46”无法再“下坠”了，这就是它的最终位置：

我们对比关键字的次数是 4 次（下坠的时候，左右孩子也要对比，和小的那个换）

现在我们要在这个堆中删除元素“65”：

被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止。

所以我们用“46”来代替被删元素：

87>78，46<78，无法再“下坠”，这就是它的最终位置，我们不用换。

我们对比关键字的次数是 2 次

---

总结

这篇选择排序中简单选择排序和堆排序都是不稳定的，第一篇插入排序中我们学的插入排序是稳定的，希尔排序是不稳定的，第二篇交换排序中我们学的冒泡排序是稳定的，快速排序是不稳定的。

简单来说，简单选择排序就是在最开始画一条线，每次都在线后面的元素中找到最小或者最大的放前面，放一个后挪一格，那么线前面的就都是有序的。这个线一个一个往后挪，直到挪到最后，线后面没东西了，我们的排序也完成了。

堆排序就是先把一个序列调整变成堆，比如大根堆，也就是找到第一个非叶子结点（从底向上找），以这个结点打头，一个一个从后往前开始调整，每次先看这个结点左右孩子谁大，谁大就和这个结点换，如果破坏了下一层的堆就继续调整，调整完就换结点，直到从第一个非叶子结点开始调整完所有非叶子结点为止。

变成堆之后，再每次把堆顶元素加入有序子序列中（逻辑视角就是和树的最后一个子结点进行交换），完了再针对交换过去的根节点进行下坠调整，调整完则一趟堆排序就完成了，到待排序序列只剩一个元素的时候整个堆排序过程就完成了。

简单选择排序时间复杂度是O(n²)，堆排序时间复杂度是O(nlog₂n)。

我们在堆里面插入元素的时候，新元素放到表尾，与新元素的双亲结点对比，若新元素比双亲结点更小，则将二者互换。新元素就这样一路“上升”，直到无法继续上升为止；

在堆里面删除元素的时候，被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止。

堆的删除需要“下坠”，和我们调整堆一样的，都是先要比左右孩子，再拿双亲结点和左右孩子中最大（小）的那个比；但是我们“上升”就不一样了，上升只需要该元素和双亲结点比就可以了，这个要注意一下。