【论文阅读34】Attention-ResNet-LSTM（JRMGE2024）

论文提出了一种新的混合深度学习模型——Attention-ResNet-LSTM，用于实时预测盾构机（TBM）的掘进速度（Advance Rate，简称AR）。该模型结合了注意力机制（Attention）、残差网络（ResNet）和长短时记忆网络（LSTM），旨在充分挖掘盾构掘进过程中复杂的时空非线性特征。

[1] Yu S, Zhang Z, Wang S, et al. A performance-based hybrid deep learning model for predicting TBM advance rate using attention-ResNet-LSTM[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2024, 16(1): 65-80.

期刊：Journal of Rock Mechanics and Geotechnical Engineering

论文题目：
一种高效混合深度学习模型用于盾构机掘进速度预测——基于Attention-ResNet-LSTM
作者：
Sihao Yu¹, Zixin Zhang¹²*, Shuaifeng Wang¹²**, Xin Huang¹², Qinghua Lei¹³⁴

作者单位：

¹ 同济大学 土木工程学院 岩土工程系（Department of Geotechnical Engineering, College of Civil Engineering, Tongji University, Shanghai, China）
² 同济大学 岩土及地下工程教育部重点实验室（Key Laboratory of Geotechnical and Underground Engineering, Ministry of Education, Tongji University, Shanghai, China）
³ 瑞士苏黎世联邦理工学院 地球科学系（Department of Earth Sciences, ETH Zürich, Zürich, Switzerland）
⁴ 瑞典乌普萨拉大学 地球科学系（Department of Earth Sciences, Uppsala University, Uppsala, Sweden）

---

1. 数据处理和特征选择：使用长江天然气管道项目的现场数据，经过预处理（数据提取、异常值检测和归一化），通过EPR算法筛选出最优输入参数组合，包括刀盘转速（RS）、推力（TH）、扭矩（TOR）、压缩模量（Es）和承载力特征值（BC）。其中推力和扭矩与掘进速度的相关性最强。

2. 模型结构设计：结合了ResNet和LSTM结构，通过注意力机制动态赋权，提升模型对不同输入特征重要性的感知和适应能力。参数调优表明使用两个ResNet层和一个LSTM层的组合效果最佳，历史数据序列长度为20分钟能兼顾准确度和计算效率。

3. 模型性能验证：与传统深度学习模型（ResNet-LSTM、LSTM、GRU、RNN）相比，Attention-ResNet-LSTM模型在掘进速度预测上的均方根误差（RMSE）和平均绝对百分比误差（MAPE）均更低，预测效果更优。

4. 复杂地层适应性测试：在包含硬软土交替地层的案例中，Attention机制显著提升了模型的预测精度和稳定性，且优于无注意力机制的ResNet-LSTM模型。

5. 泛化能力验证：模型在深圳白芒河隧道项目的独立数据集上表现出良好的迁移能力和自适应能力，能够在新工程和不同地质条件下保持高预测准确度。

6. 未来展望：随着更多隧道工程数据的积累，模型有望进一步提升预测能力，帮助盾构机操作人员实时调整参数，实现更安全高效的掘进。

简而言之，论文提出了一种融合注意力机制的混合深度学习模型，能更准确地预测盾构机掘进速度，并具备较强的适应性和泛化能力，适用于复杂地质条件和不同工程场景。

---

文章历史：

• 收稿日期：2022年11月24日
• 修回日期：2023年4月18日
• 接收日期：2023年6月15日
• 在线发布日期：2023年8月2日

摘要

隧道掘进机（TBM）技术已广泛应用于全球地下工程施工中，然而，如何确保TBM掘进过程的安全性与高效性依然是当前的主要关注点。掘进速度是反映TBM施工过程及其与围岩相互作用的重要参数，可靠的掘进速度预测有助于优化TBM施工性能。
本文提出了一种基于 Attention-ResNet-LSTM 的混合神经网络模型，用于精准预测TBM掘进速度。模型训练与测试数据源自长江天然气管道穿越工程，包含了地质参数和TBM施工参数。同时，采用进化多项式回归（evolutionary polynomial regression, EPR）方法辅助选择输入变量。
数值实验结果表明，本文提出的 Attention-ResNet-LSTM 模型相较于常用的智能预测模型，具有更低的均方根误差（RMSE）和平均绝对百分比误差（MAPE），预测性能更优。此外，本文还开展了参数化分析，探讨历史数据序列长度与模型结构对预测精度的影响，并实施了输入输出变量相关性分析，为调整TBM施工参数提供指导依据。
该混合智能模型在复杂地层条件下TBM掘进案例中得到了应用验证。最后，采用来自中国深圳白芒河隧道项目的数据对模型的泛化能力进行了进一步测试。结果表明，本文模型凭借其自适应特性，在未知数据场景下相较于传统ResNet-LSTM模型表现出更优的预测能力。
关键词：
隧道掘进机 (TBM)、掘进速度、深度学习、Attention-ResNet-LSTM、进化多项式回归

---

1. 引言

随着全球对地下空间开发利用程度的不断提高，隧道掘进机（Tunnel Boring Machine，TBM）技术因其高机械化程度、优良的施工效率以及较低的环境影响，已被广泛应用于各类地下工程项目（Yagiz, 2017；Zhang 等, 2017, 2020a, b, 2022a；Gao 等, 2019；Liu 等, 2019）。然而，由于复杂的TBM-围岩相互作用关系，TBM在掘进过程中其性能常常存在波动，操作人员需依赖经验实时调整掘进参数，这在实际工程中容易导致较大的不确定性和不可预知的风险（Rostami, 2016；Cardu 等, 2021）。因此，为提高TBM施工过程的安全性与效率，准确及时地预测TBM性能至关重要（Yang 等, 2022；Zhang 等, 2022b）。

通常，TBM性能主要由两个关键参数表征，即掘进速度（Advance Rate, AR）和贯入力，后者定义为掘进速度与刀盘转速之比。其中，掘进速度反映了TBM与围岩之间的相互作用，直接影响施工总工期与成本，因此，其稳健预测对于隧道工程尤为重要（Elbaz 等, 2020；Wang 等, 2020；Fu 和 Zhang, 2021）。

以往学者已提出多种经验模型（Yagiz, 2008；Gong 和 Zhao, 2009；Delisio 等, 2013；Fatemi 等, 2018）和理论模型（Farmer 和 Glossop, 1980；Sanio, 1985；Hughes, 1986；Rostami 和 Ozdemir, 1993；Rostami, 1997）用于TBM性能预测。经验模型主要基于对历史工程数据的回归分析建立TBM-围岩关系，但其在其他工况或具体工程项目中的适用性通常存在较大不确定性。理论模型则假定圆盘刀具与开挖面之间的作用力分布满足简化的线性或高斯分布，并基于切削试验数据进行校准，但难以全面考虑复杂地层条件下的TBM-围岩相互作用，因而限制了其在实际工程中的应用价值（Rostami 和 Ozdemir, 1993；Rostami, 2013；Labra 等, 2017）。

近年来，数据采集与传输技术的快速发展，使得工程师能够获取大量来自TBM施工过程的原始数据，这为采用先进的机器学习方法开展TBM性能预测提供了契机（Sheil 等, 2020）。例如，Salimi 等（2016）利用自适应神经模糊推理系统与支持向量回归方法预测TBM掘进速度；Armaghani 等（2018）基于基因表达式程序设计方法，结合马来西亚Pahang-Selangor原水输水隧道工程数据估算TBM性能；Koopialipoor 等（2019）构建了基于深度神经网络的模型预测TBM贯入力，较传统模型表现出更高精度。Zhou 等（2021）采用极限梯度提升与贝叶斯优化相结合的方法，基于1286组数据预测硬岩地层中的TBM掘进速度。Sun（2022）提出基于支持向量机与改进粒子群算法的盾构掘进参数匹配模型，为施工参数优化提供指导。Wang 等（2022）开发了基于极限梯度提升方法的在线TBM贯入力预测平台，预测精度良好。Mahmoodzadeh 等（2022）采用灰狼优化算法增强的LSTM混合模型，基于1125组数据预测TBM贯入力。Fu 等（2023）设计了结合图卷积网络与LSTM的深度学习模型，用于预测TBM纵向与横向偏差。Yu 等（2023）基于注意力机制，建立了双路径残差网络模型预测TBM利用系数（掘进速度与推进速度之比）。Song 等（2023）基于鲸鱼优化算法，开发了命名为“stacking框架”的混合智能模型，预测性能优于多种主流机器学习方法，泛化能力较强。Wang 等（2023a）构建了结合极限梯度提升（XGBoost）与半理论模型的集成模型预测TBM贯入力。Wang 等（2023b）提出了一种数据驱动的多步TBM姿态预测模型，称为卷积门控循环联合神经网络，可在21步内稳定实现高精度预测。

在所有机器学习方法中，深度学习算法因其无需先验假设即可提取多维非线性特征的能力，近年在TBM性能预测中得到广泛应用。表1汇总了已有基于深度学习的TBM性能预测研究工作。值得注意的是，现有多数研究通常基于传统前馈神经网络，辅以粒子群优化等方法克服训练过程中的收敛性问题，预测掘进速度或贯入力。其中，长短期记忆网络（LSTM, Hochreiter 和 Schmidhuber, 1997）常用于提取TBM施工过程中长期、时变的原始数据特性，提升预测精度（Fu 和 Zhang, 2021；Wang 等, 2021；Guo 等, 2022）。

尽管深度学习模型已被广泛应用于TBM性能预测，但依然存在一定局限性。一方面，模型在复杂地层条件或噪声干扰较大的数据环境下预测精度易降低；另一方面，深度神经网络存在“模型退化”问题，即随着网络层数增加，预测精度达到峰值后反而下降（He 等, 2016；Qin 等, 2021；Shi 等, 2021）。

为克服上述问题，本文提出了一种新型性能驱动的混合深度学习模型。该模型利用LSTM充分提取TBM施工过程中的时间依赖特性，通过ResNet（He 等, 2016）提取掘进环境的空间非线性特征，且ResNet中的残差连接结构可有效缓解多层神经网络模型退化问题。此外，模型引入注意力机制，根据不同地质条件自适应生成输入权重，提升模型泛化能力。注意力机制作为当前人工智能领域研究热点，已被应用于机器翻译（Choi 等, 2018）、动作识别（Tian 等, 2019）、文本分类（Liu 和 Guo, 2019）等多个任务。近期，该机制也被集成至TBM性能预测模型中，用于动态聚焦关键数据特征。例如，Pan 等（2022）提出了基于注意力机制的图卷积网络预测贯入力与能耗，性能优于其他机器学习方法；Chen 等（2022）采用时间模式注意力检测结构与注意力机制模块预测TBM掘进参数，效果优于基准Transformer模型。然而，目前基于注意力机制的模型在处理全新数据集时的泛化能力尚不明确。

为全面捕捉长期TBM掘进过程中复杂、非线性与时变特性，本文提出一种基于性能驱动的混合深度学习模型用于实时预测TBM掘进速度。模型利用ResNet与LSTM分别处理原始数据的空间与时间特征，并基于注意力机制自适应调整不同输入参数权重，同时通过进化多项式回归（EPR）方法确定最优输入参数组合。基于长江天然气管道穿越工程数据验证模型有效性，随后分析历史数据序列长度与模型结构对预测精度的影响，并探讨输入与输出变量间的相关性。最后，以深圳白芒河隧道工程数据对模型泛化能力进行测试。

---

2. 方法学

2.1 卷积神经网络（CNN）与残差网络（ResNet）

卷积神经网络（Convolutional Neural Network, CNN）具备强大的特征提取能力，其结构主要由卷积层与池化层构成。卷积层对输入数据进行局部卷积操作，池化层则实现特征维度的压缩（如图 1 所示）。经卷积和池化操作后的变换结果称为特征图（feature map），可有效揭示与待解决问题相关的关键特征（Xue 和 Li, 2018；Kattenborn 等, 2021）。

残差网络（Residual Network, ResNet）是一种特殊形式的CNN，通过引入残差学习（residual learning）技术，解决了常规深层CNN存在的退化问题（He 等, 2016）。ResNet的基本单元如图 2 所示，其定义如下：

$$H(x)=F(x)+x$$

其中，$x$ 和 $H(x)$ 分别表示输入和输出向量，$F(x)$ 表示待学习的残差映射函数。ResNet并不直接学习 $H(x)$ 与 $x$ 之间的映射关系，而是通过恒等捷径连接（identity shortcut connection）构建残差函数 $F(x)$。当ResNet浅层部分已充分提取目标特征后，网络深层部分的残差映射 $F(x)$ 将在训练过程中趋于0，从而避免深层神经网络中的性能退化现象。因此，本文模型中采用ResNet对输入特征进行空间特征提取。

2.2 长短期记忆网络（LSTM）

长短期记忆网络（Long Short-Term Memory, LSTM）是一种特殊的循环神经网络（Recurrent Neural Network, RNN），广泛应用于自然语言处理领域，如语义分析与机器翻译。传统RNN结构如图3所示，当前时刻隐藏层单元的值由当前输入与上一时刻隐藏单元共同决定，因此具备存储历史信息的能力。然而，当输入序列较长时，RNN在反向传播过程中容易出现梯度消失或梯度爆炸问题。LSTM通过引入记忆单元（memory cell）有效解决了该问题。记忆单元内部设计有门控机制（gate）以处理并保存重要的时间序列信息（Hochreiter 和 Schmidhuber, 1997）。典型的LSTM单元结构如图 4 所示，包括遗忘门（forget gate）、输入门（input gate）与输出门（output gate）三个主要部分。

各门控单元计算公式如下：
遗忘门：
$$f_t=\text{sigmoid}(W_f\cdot [h_{t-1},x_t]+b_f)$$
输入门：
$$i_t=\text{sigmoid}(W_i\cdot [h_{t-1},x_t]+b_i)$$
输出门：
$$o_t=\text{sigmoid}(W_o\cdot [h_{t-1},x_t]+b_o)$$
当前单元状态更新：
$${\tilde{C}}_t=\tanh (W_c\cdot [h_{t-1},x_t]+b_c)$$
当前记忆单元状态：
$$C_t=f_t\times C_{t-1}+i_t\times {\tilde{C}}_t$$
当前单元输出：
$$h_t=\tanh (C_t)\times o_t$$
其中，$W\_f$、$W\_i$、$W\_c$ 和 $W\_o$ 分别为各门控单元的权重矩阵，$b\_f$、$b\_i$、$b\_c$ 和 $b\_o$ 为偏置项。$\text{sigmoid}(x)=\frac{1}{1+e^{-x}}$，$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$，符号 $\times$ 表示Hadamard积（元素对应相乘）。$\tilde{C}\_t$ 和 $C\_t$ 分别表示候选单元状态与当前更新单元状态。所有参数在各时间步内保持共享。本文模型中，LSTM用于进一步提取多维特征中的时间依赖性信息。

2.3 注意力机制（Attention Mechanism）

注意力机制（Attention Mechanism）灵感源于人类生物系统，即在处理复杂问题时，人类会迅速聚焦于最具辨识度与意义的关键信息（Niu 等, 2021；Pan 和 Zhang, 2022）。传统神经网络在完成训练后，得到的权重矩阵固定，即使接收到完全不同的新输入，这些权重也不随环境变化调整，因此，传统神经网络模型难以适应复杂动态环境（Irie 等, 2022）。
通过引入注意力机制，神经网络能够根据输入数据动态生成自适应权重，从而聚焦于输入中最相关的部分。迄今为止，已有多种注意力机制方法被提出，本文模型中采用通道注意力机制（channel attention）与时间注意力机制（temporal attention）相结合的方式，以实现对关键特征的自适应加权。

2.3.1 通道注意力机制（Channel Attention）

如前所述，ResNet 能够通过卷积操作从多维输入中提取丰富的特征，这一过程融合了空间信息与通道信息。已有研究表明，通过显式建模特征图通道间的依赖关系，可以进一步提升网络性能。因此，本文在 ResNet 中引入通道注意力机制，对各通道特征赋予自适应权重，以实现通道特征的动态重标定。该权重参数可通过反向传播进行训练。
为实现该操作，本文采用 Hu 等（2018）提出的 Squeeze-and-Excitation (SE) 模块。在“压缩（squeeze）”阶段，利用全局平均池化（global average pooling）生成通道特征汇聚信息；随后在“激励（excitation）”阶段，使用两个全连接层（fully connected, FC）捕捉通道间依赖关系，同时限制计算复杂度。其中，第一层 FC 根据预设缩减比对输入维度降维，第二层 FC 恢复至原始通道维度。最后，通过通道权重与来自 ResNet 的特征图逐通道相乘，得到通道注意力模块的输出（Hu et al., 2018）。

2.3.2 时间注意力机制（Temporal Attention）

在经典的 LSTM 时序预测任务中，通常直接将最后时刻的隐藏状态作为最终输出。然而，随着输入序列长度增加，预测精度会显著下降（Bahdanau et al., 2015）。为解决该问题，本文在最后一层 LSTM 后加入时间注意力层，使所有时间步的隐藏状态均参与预测。
具体做法是：将最后时刻隐藏状态设为标准状态，依次与各时刻隐藏状态进行对比，计算对应的注意力得分（score）。得分越高的隐藏状态将获得更高的权重，网络便能动态聚焦于更具信息性的特征，从而提升对长短期序列的适应性。其计算过程如下：
注意力得分：

$$\text{score}(h_t,h_T)=v^T\tanh (W[h_t,h_T])$$
注意力权重：
$$a_t=\frac{\exp (\text{score}(h_t,h_T))}{{\sum }_{k=1}^T\exp (\text{score}(h_k,h_T))}$$
时间注意力输出：
$$h_o=\sum _{t=1}^T{a}_t{h}_t$$
其中，$h\_t$ 为第 $t$ 个时间步的隐藏状态，$h\_T$ 为最后一个时间步的隐藏状态，$a\_t$ 为第 $t$ 个时间步对应的注意力权重，$v$ 和 $W$ 为可学习参数矩阵。上述 score 函数参考 Luong 等（2015）。

---

2.4 表达式回归（EPR）

表达式回归（Expression Programming-based Regression, EPR）是一种融合了常规模型回归与基于遗传编程的符号回归（symbolic regression）方法，适用于描述多输入与多输出变量之间的相关性（Giustolisi 和 Savic, 2006）。本文中，EPR 被用于特征选择，主要分为两步：

第一步，利用遗传算法搜索多项式的符号表达式，变换后的变量可表示为：
$$z_j=x_{ES(j,1)}^{m_1},x_{ES(j,2)}^{m_2},\dots ,x_{ES(j,k)}^{m_k}$$

其中，$x\_i$ 表示第 $i$ 个输入变量，$k$ 为输入变量个数，$ES\_m\times k$ 为遗传算法获得的指数矩阵，$z\_j$ 表示第 $j$ 个变换变量，$m$ 为变换变量个数，可人工设定。需要说明的是，也可采用粒子群优化（PSO）等其他优化算法替代遗传算法。

第二步，对多项式中各项系数执行最小二乘线性回归，最终表达式为：
$$y=\sum _{j=1}^m{a}_j{z}_j+a_0$$

其中，$y$ 为预测值，$a\_j$ 为第 $j$ 个变换变量的回归系数，$a\_0$ 为常数项。

2.5 评价指标

为评估预测模型性能，本文采用平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）与均方根误差（Root Mean Square Error, RMSE）作为评价指标。MAPE 与数据量纲无关，但当真实值趋近于 0 时，MAPE 容易趋于无意义的无穷大。RMSE 则依赖于数据尺度，可直接反映预测误差。因此，二者结合可全面衡量模型性能。MAPE 与 RMSE 越小，预测精度越高，预测值与实测值偏差越小。
其计算公式如下：
MAPE：

$$\text{MAPE}=\frac{1}{n}\sum _{i=1}^n\left|\frac{y_i-{\hat{y}}_i}{y_i}\right|$$
RMSE：
$$\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}$$

其中，$n$ 为样本总数，$y\_i$ 与 $\hat{y}\_i$ 分别为第 $i$ 个样本的实测值与预测值。
此外，为更全面评价模型表现，本文还引入决定系数（Coefficient of Determination, $R^2$）：

$$R^2=1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}$$
其中，$\bar{y}$ 为样本均值。值得注意的是，$R^2$ 未参与模型优化过程，仅作为不同预测模型对比时的附加评价指标。

2.6 混合智能模型

本文基于第 2.1–2.5 节所述方法，构建了一种 Attention-ResNet-LSTM 深度学习模型（图 5）。模型包括 ResNet 模块、LSTM 模块与两个注意力模块（通道注意力与时间注意力）。其中，ResNet 模块包含步长为 1、填充为 1、卷积核尺寸为 3 的卷积层，LSTM 模块包括若干 LSTM 层与用于调整维度的全连接层。
首先，利用 ResNet 提取输入数据中的非线性空间特征。其次，将特征图输入通道注意力模块，计算通道依赖关系权重，进行逐通道加权。然后，将加权后的特征输入 LSTM 层，捕捉长期与时变依赖关系。在最后一层 LSTM 后，加入时间注意力层，计算注意力输出 $h\_o$。最终，将 $h\_o$ 与最后时刻隐藏状态（图 5 中的 $h\_T$）拼接，输入全连接层，获得最终预测结果。

ResNet 块数量 $m$ 与 LSTM 层数 $n$（图 5 中所示）为模型超参数，需通过后续实验确定。

3. 数据库

3.1 数据来源

本研究所用数据来自长江天然气管道穿越工程。该管道线路穿越江苏省南通市与常熟市之间的长江段，穿越长度约为 10.23 km，是整个工程的关键控制性项目。为了保障盾构机在高水压及高土压环境下掘进施工的面部稳定性，采用了泥水压平衡盾构（Slurry Pressure Balance Shield TBM）进行穿越作业。隧道内外直径分别为 6.8 m 与 7.6 m，管片厚度为 0.4 m，宽度为 1.5 m。图 6 显示了工程区域的地质剖面。

盾构掘进过程中，TBM 的操作参数以 1 Hz 的频率实时记录，累计获得了约 1760 万组数据。

3.2 数据预处理

原始数据体量极大，且包含大量无效数据与噪声，直接用于模型训练存在困难。此外，不同数据量纲差异显著，必须在输入模型前对原始数据进行预处理（Xiao et al., 2022）。

3.2.1 数据抽取

TBM 掘进参数通过数据采集与传输系统以 1 Hz 频率自动记录。然而，直接使用全部原始数据进行预测建模不仅计算代价高昂，也无实际必要。为平衡计算效率与信息完整性，首先将原始数据重采样为 1 min 时间间隔（对比分析表明，重采样数据已足以保留原数据的主要特征）。
此外，TBM 停机期间产生大量空值数据，这些空值同样记录在原始数据集中。为构建干净的数据集，需在首步剔除这些空值。本文采用 Zhang 等（2020b）提出的空值检测算法，计算：

$$F_i=T{H}_i\times TO{R}_i\times A{R}_i\times R{S}_i$$
其中，$TH\_i$、$TOR\_i$、$AR\_i$ 和 $RS\_i$ 分别为第 $i$ 个时刻盾构机的推力、主轴扭矩、掘进速度和刀盘转速。若 $F\_i=0$，判定该时刻盾构机处于非工作状态，相应数据即从数据集中剔除。

3.2.2 异常值检测

TBM 掘进过程中的部分数据可能因外部干扰或传感器故障而产生异常值。本文采用 Mahalanobis 距离（Mahalanobis, 1936）作为异常值识别标准。与欧氏距离不同，Mahalanobis 距离能消除变量间相关性，适用于多变量时间序列异常值检测。

设多元序列：
$$x=(x_1,x_2,\dots ,x_n{)}^T$$
均值向量：
$$m=(m_1,m_2,\dots ,m_n{)}^T$$
协方差矩阵 $S$，则 Mahalanobis 距离计算公式为：
$$D_M(x)=\sqrt{(x-m{)}^T{S}^{-1}(x-m)}$$
当所有变量互不相关时，$S$ 为单位矩阵，Mahalanobis 距离即等于欧氏距离。本文取 Mahalanobis 距离的 0.9 分位值作为异常值判别阈值（Zhang et al., 2020a），即大于该阈值的样本判定为异常值并剔除。图 7 展示了 TBM 掘进速度序列中异常值的检测结果（红圈所示）。

3.2.3 数据归一化

为消除不同变量量纲差异并加速模型收敛，对所有变量进行归一化，将其映射至 [0,1] 区间。设某参数 $x$，其归一化结果 $x\_norm$ 计算公式为：

$$x_{norm}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

其中，$x\_max$ 和 $x\_min$ 分别为该变量的最大值与最小值。神经网络训练完成后，预测输出需还原至原始空间。

3.3 输入参数选择

经过预处理后的数据集仍包含逾 100 个操作参数。若将全部参数作为模型输入，会极大增加模型复杂度与计算耗时；而输入参数不足又会使模型难以充分学习输入与输出间的复杂关系，导致预测精度不足。因此，需在模型训练前合理筛选输入特征。

通常，应优选与预测目标具有强相关性的参数作为神经网络输入，以保证预测性能同时尽可能简化模型结构。已有研究采用多种方法筛选输入参数。例如，Li 等（2022）基于皮尔逊相关系数量化变量间线性相关性，剔除相关系数接近 0 的变量；Zhang 等（2020a）基于灰色关联度（Deng, 1982）衡量变量发展趋势的一致性，选取关联度较高的特征。但上述方法仅能度量两变量间一对一相关性，神经网络属于多输入-单输出映射模型，因此需综合考察不同输入参数组合对预测标签的相关性。

本文采用 EPR 方法（见第 2.4 节）筛选输入参数，其优势在于能量化多个输入参数组合与目标输出间的相关性。此外，将地质参数——压缩模量 $E\_s$ 与承载力特征值 $BC$ 纳入数据库。前者反映地层在荷载作用下的变形特性，后者是反映土层强度及承载能力的重要指标，通常通过平板载荷试验确定，即取土压力-变形曲线线性段内规定变形量所对应的压力值。

掘进速度 $AR$ 作为 TBM 性能表征指标，无法由操作人员直接调节，其高度依赖可调节的盾构操作参数（Liu et al., 2021）。根据 Wang 等（2020）和 Zhang 等（2020b）推荐，本文选择刀盘转速 $RS$、推力 $TH$、主轴扭矩 $TOR$ 和仓内泥浆压力 $SPW$ 作为备选输入参数。此外，刀具磨损程度可能对掘进性能产生影响，但通过常规掘进周期及时更换刀具可有效消除该影响，故本研究不考虑刀具磨损对 $AR$ 的作用（Liu et al., 2017；Ren et al., 2018；Zhao et al., 2019；Karami et al., 2021）。

不同参数组合的 EPR 计算结果如图 8 所示。其中，$RS$、$TOR$、$TH$、$BC$ 与 $E\_s$ 的组合在最少迭代次数内取得目标函数最小值，即在最短时间内达到最小预测误差，同时这些参数均可由盾构机操作人员实时调节。仅 $TOR$ 与 $TH$ 的组合也表现出较强相关性。单变量方面，$TH$ 是影响 $AR$ 的最主要因素，与工程经验高度一致。

最终，本文基于 EPR 选择 $RS$、$TOR$、$TH$、$BC$、$E\_s$ 以及 $AR$ 自身作为模型输入参数。需说明，若换用其他项目数据，最优输入参数组合可能略有差异。但基于大量掘进工程经验，影响 TBM 性能的主控因素基本固定，即推力、扭矩、刀盘转速与地质条件（Fu 和 Zhang, 2021；Liu et al., 2021；Pan et al., 2022），故上述参数组合具有较好的跨项目适应性。

4. 实验与结果分析

4.1 数据集划分

首先，从预处理后的数据集中提取时间序列作为预测模型的输入。采用滑动窗口法（sliding window）对数据集进行分割，滑动步长设为 1，窗口长度设定为 20，后续可作为超参数进行优化调整。

预测目标为第 $t$ 个时刻的掘进速度 $AR$，对应预测函数可表示为：

$$A{R}_j^t=f\left({\left\{h(RS,TH,TOR,E_s,BC,AR{)}_{j,t-k}\right\}}_{k=19}^0\right)$$

其中：

• $h(\cdot )$ 表示输入特征的组合函数（可理解为向量拼接等预处理操作）；
• 花括号 $\cdot \_{k=19}^0$ 表示从 $t-19$ 到 $t$ 这20个连续时间步的特征序列；
• $f(\cdot )$ 是预测模型映射函数，输出掘进速度。

需注意，历史掘进速度 $AR$ 也作为输入特征，以帮助模型充分利用历史信息，提升预测精度。

随后，将数据集按照 8:1:1 的比例划分为训练集、验证集与测试集（关于该比例选取依据详见附录 A）。训练集用于模型训练，验证集用于超参数优化，测试集用于最终模型性能评估。

4.2 模型构建与训练

所有实验均基于 PyTorch 深度学习框架完成，运行环境为搭载 AMD Ryzen 5800X 4.60 GHz 处理器、16 GB 内存及 NVIDIA GeForce RTX 3080 显卡的工作站。模型训练采用全监督方式，基于误差反向传播（Backpropagation）算法进行。

为防止过拟合，训练过程中引入提前停止策略（Early Stopping）。同时，采用随机搜索法（Random Search）确定模型最优超参数组合，随机搜索次数设定为 100。

为验证所提 Attention-ResNet-LSTM 模型性能，将 ResNet-LSTM、LSTM、GRU 及 RNN 模型作为对比对象进行性能比对。所有模型均使用 Adam 优化算法。
各神经网络模型的超参数搜索范围及最终确定的最优超参数组合分别列于表 2 和表 3 中。

4.3 结果分析

各神经网络模型在测试集上的预测结果如图 9 所示，其性能指标列于表 4 中。在图 9 中，左侧折线图对比了实测值与预测值随预测点变化的关系；中间柱状图展示了在 1 mm/min 区间内，实测值与预测值数量的差异分布；右侧散点图显示了预测值与实测值的拟合关系，实线表示理想预测线（斜率为 1）。

从图 9(a) 可以看出，Attention-ResNet-LSTM 模型能够准确捕捉掘进速度 ($AR$) 的变化趋势，其均方根误差 (RMSE) 和平均绝对百分比误差 (MAPE) 分别为 1.31 mm/min 和 1.52%，预测值与实测值基本吻合。即使在 $AR$ 局部波动剧烈的情况下，该模型也能高精度预测极值点。此外，该模型预测值的分布与实测值最为接近。
ResNet-LSTM 模型的 RMSE 为 1.38 mm/min，略高于 Attention-ResNet-LSTM 模型。散点图显示该模型对 $AR$ 的预测值与理想线较为接近，具备良好预测性能，但柱状图表明 ResNet-LSTM 模型在 55 mm/min 附近的预测次数明显多于实测值（图 9(b)）。
相比之下，LSTM 和 GRU 模型的预测性能较差，部分预测值与实测 $AR$ 偏差较大（图 9© 和 (d)）。折线图显示，这两种模型主要对局部峰值敏感，而对非峰值段预测效果较差。
所有模型中，RNN 模型的预测精度最低（图 9(e)），其预测值普遍高于实测值，RMSE 和 MAPE 分别为 2.82 mm/min 和 4.69%，明显劣于其他模型。
需要指出的是，所有模型在预测 $AR$ 低于 40 mm/min 区段的表现均较差。此部分数据可能由 TBM 堵塞或异常操作引发，预测难度较大。
此外，本文在表 5 中列出了各模型的判定系数 ($R^2$)。总体来看，$R^2$ 分析结果与 RMSE 和 MAPE 指标趋势一致，作为训练过程中模型性能评估参数。然而，各模型的 $R^2$ 值均偏低，尤其是 RNN 模型，主要原因有二：

1. $R^2$ 与样本均值相关，数据分散性对该指标影响较大。本数据集中大部分 $AR$ 值分布于 50–65 mm/min 区间，导致整体 $R^2$ 偏低。
2. 部分异常数据由 TBM 的突然启停或不当操作产生，模型难以精确预测该类点值，导致 $R^2$ 偏低。

本文所选对比模型均为时序预测常用算法（Cai et al., 2019；Abbasimehr et al., 2020；Qin et al., 2022），具备可比性。需特别说明的是，较低的 RMSE 和 MAPE 以及较高的 $R^2$ 通常代表同一数据集上预测性能更优。

综上，Attention-ResNet-LSTM 和 ResNet-LSTM 模型在测试集上预测性能优于其他模型，二者的详细对比分析将在第 5 节展开。

此外，表 4 中列出了各模型每轮训练的耗时，结果表明更高的预测精度通常伴随更长的计算时间，Attention-ResNet-LSTM 模型单轮训练耗时 48.12 s，约为 RNN 模型的 12 倍。因此，在计算资源受限场景下，仍可考虑使用 LSTM 或 GRU 进行快速预测。

为了进一步分析 Attention-ResNet-LSTM 模型误差分布特性，绘制了其误差小提琴图与直方图（图 10）。由小提琴图可见，当 $AR$ 小于 40 mm/min 或处于 40–50 mm/min 区间时，预测误差相对较高，尤其在 40 mm/min 以下，预测误差均值接近 16 mm/min，这也是 $R^2$ 偏低的重要原因。相反，当实测 $AR$ 超过 50 mm/min 时，预测误差主要分布于 0–2 mm/min 范围内。

图 10(b) 显示，实测 $AR$ 数据大多集中于 50–65 mm/min，40 mm/min 以下数据占比较少。因此，测试集上的误差分布与训练数据分布密切相关，若未来能够增加 40 mm/min 以下数据的数量，模型预测精度有望进一步提升。

5. 讨论

5.1 模型应用

我们在第4.3节中验证了所提出预测模型的良好性能。然而，在实际工程项目中，模型应能够提供较长时间范围内的预测结果（如未来1060 min），而不仅是下一分钟的预测。为实现多步预测，我们采用递归方法。假设通过式 (17) 得到了第 $t$ 个时刻的预测AR值，则该预测值可以作为输入导入模型，进而预测第 $t+1$ 个时刻的AR。通过重复该过程，便可实现TBM性能的长期预测。为了确定模型可预测的最长时间窗口，我们对测试集中的10个不同数据段进行长期预测试验。图11展示了RMSE随预测时间区间（步长5 min）变化的趋势。图中，水平短横线和方形标记分别表示95%置信区间和均值，红色虚线连接各个时刻的均值。结果表明，当预测时间小于约25 min时，误差增长较慢且幅值较小。然而，当预测时长达到2535 min（图11阴影区）时，RMSE明显增加，表明预测精度急剧下降。同时，超过25 min后竖线长度也增加，反映出模型预测逐步变得不稳定。其原因可能是递归预测过程中误差逐步累积，最终导致多步预测失效。综上，所提模型可在较高精度下对TBM性能进行最长约25 min的长期预测，实际掘进中，操作人员可在此预测时段内调整推力、扭矩等参数，以保障掘进效率。

5.2 序列长度影响

在第4.1节中，我们将序列长度设为20 min，即将20 min数据序列作为神经网络输入。本节对该参数进行敏感性分析，因为其对预测结果有显著影响。若历史序列过短，模型无法获取足够信息，预测精度降低；反之，序列过长则会显著增加输入特征复杂度，导致模型难以提取有效特征。通常，可通过偏自相关函数（PACF）分析时间序列 $x\_t$ 与 $x\_t-k$ 之间的相关性（Ghimire et al., 2019）。对数据库中AR序列进行PACF分析，结果如图12所示。位于两条蓝线之外的数据点表示与当前值 $x\_t$ 具有统计显著相关性。可见，偏自相关系数随滞后时间递减，约在30 min滞后处衰减至0，随后基本保持不变。由此可推断，超过30 min滞后的历史数据对当前AR值影响甚微。因此，我们将序列长度依次设为10、15、20、25和30 min，探讨其对预测精度的影响。结果如图13所示，训练每个epoch所需时间随序列长度线性增加，从10 min序列的37.45 s上升至30 min序列的55.43 s。预测精度与序列长度之间未表现出显著相关性，20 min序列的模型在测试集上取得最低RMSE值1.308 mm/min。当序列长度减小时，误差迅速增加，原因可能是模型无法从有限历史数据中获取充分信息。因此，将序列长度设为20 min较为适宜，能够在保证预测精度的同时，兼顾计算开销。

5.3 模型结构影响

ResNet与LSTM层数对模型性能存在一定影响。为获得最优结构，本节对这两个关键超参数进行敏感性分析。

5.3.1 ResNet层数

图14展示了ResNet层数（基本块数量）与预测精度之间的关系。ResNet层数增加，训练每个epoch耗时呈线性上升，从48.12 s增至87.66 s。模型预测误差先略微下降，随后显著上升。当ResNet层数为3层时，模型预测精度最高，RMSE为1.305 mm/min，略优于2层时的1.308 mm/min。因此，综合预测精度与计算代价，我们最终将ResNet层数设定为2层。

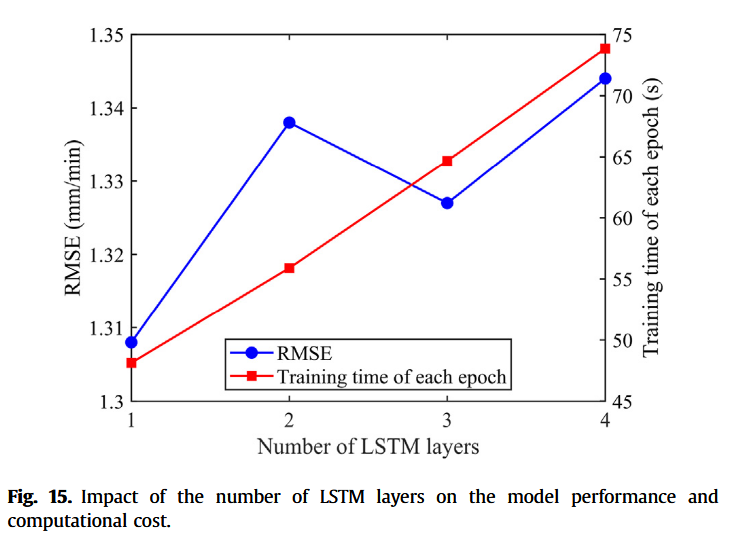
5.3.2 LSTM层数

图15所示结果与ResNet类似，LSTM层数增多，计算时间线性增长，从单层的48.12 s增至4层的73.86 s。预测精度方面，LSTM层数对模型影响不大，RMSE在1.308~1.344 mm/min间波动。因此，堆叠LSTM层数虽显著增加计算资源消耗，但对预测性能提升有限。综合考虑，单层LSTM足以满足模型需求。

5.4 输入与输出参数相关性分析

盾构操作人员无法直接调整AR值，而是通过改变TBM作业参数（如RS、TOR、TH）间接影响AR。因此，有必要分析输入参数与输出AR之间的相关性，为掘进作业提供指导。否则，即便模型给出精确预测值，操作人员也难以有效调整。Wang et al. (2020) 与 Fu 和 Zhang (2021) 研究发现，第 $t-1$ 时刻的输入对第 $t$ 时刻AR影响最大，图12亦证实了此结论。因此，我们在$t-1$时刻将单个输入参数从最小值调节至最大值，其余保持不变，分析输入与输出关系。结果如图16所示。图16a表明，随着RS增加，AR先略有下降，随后持续上升。TOR与TH表现出不同模式（见图16b、c）：两者升高均伴随AR下降。当TOR超过1500 kN·m，AR下降趋势趋缓；而TH-AR曲线在TH约3700 kN处由缓变陡。上述结论亦与工程经验一致，即较大TOR或TH值通常反映地层坚硬，TBM AR值相应降低。

5.5 不同地层下的模型性能

长距离掘进过程中，地层条件可能显著变化，导致AR剧烈波动。如图17所示，约在第2140个预测点处，地层由硬黏土突变为软黏土，实测AR值骤降。为验证模型在两种地层下的性能，分别采用Attention-ResNet-LSTM与ResNet-LSTM模型进行预测，误差指标列于表5。Attention-ResNet-LSTM在硬、软黏土下均优于基线模型，且硬黏土误差略小于软黏土，如RMSE分别为2.31 mm/min与2.96 mm/min，可能因训练集中硬黏土掘进数据占多数。总体上，前者模型RMSE与MAPE分别为2.52 mm/min与3.48%，优于后者2.79 mm/min与4.39%。图17内嵌图显示，Attention-ResNet-LSTM对硬、软黏土均表现优异，且能准确捕捉AR突降趋势。相比之下，ResNet-LSTM在第2140点附近表现较差。说明所提模型可根据输入特性动态调整权重，具备更强地质适应性。

5.6 泛化能力

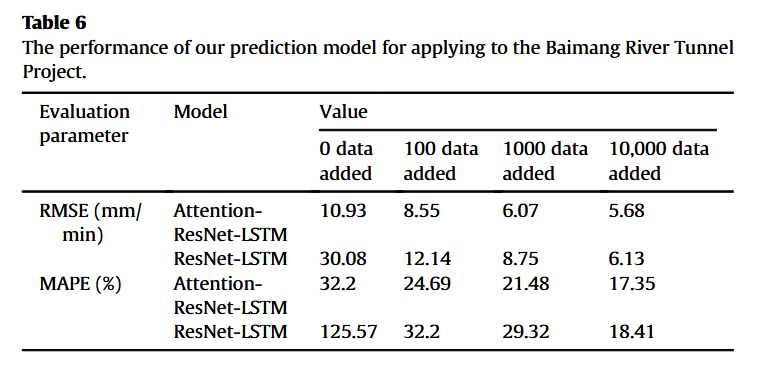
为检验Attention-ResNet-LSTM模型的泛化能力，进一步在未知数据集上验证预测性能。新数据来自深圳白芒河隧道项目，全长3366 m，含2244环管片，采用EPB盾构（Xu et al., 2022），隧道主要穿越残积土和风化花岗岩（见图18）。该项目地质条件与长江天然气管道项目完全不同。为全面评估模型稳健性，我们分别向原训练集中加入0、100、1000、10000条白芒河隧道数据，若新增数据不为0，则基于新训练集重新训练模型，测试集均为白芒河隧道数据。ResNet-LSTM作为基线模型，测试结果如表6。结果表明，随着新增数据量增多，模型预测精度逐步提升，智能模型能逐渐学习白芒河隧道地层与施工信息。相比之下，ResNet-LSTM性能波动较大，RMSE介于30.08~6.13 mm/min间，而Attention-ResNet-LSTM始终保持较低预测误差，展现出良好泛化性。当训练集仅含长江项目数据时，Attention-ResNet-LSTM在新测试集上的RMSE为10.93 mm/min，远优于ResNet-LSTM。随着数据量增加，预测误差持续降低，当新增10000条数据时，RMSE与MAPE分别降至5.68 mm/min与17.35%。综上，若应用于完全不同项目且无额外训练数据，Attention-ResNet-LSTM性能远优于ResNet-LSTM，且相较表4，所有误差指标有所增加，源于地质差异。所提模型可自适应不同输入，表现优异，若其他预测模型欲达到相似性能，至少需新增约1000条新项目数据。未来计划建设涵盖多种地质条件的大型数据库，进一步提升模型训练效果与泛化能力。毫无疑问，Attention-ResNet-LSTM凭借高效特性，可在有限数据条件下取得令人满意的预测性能。

6. 结论

本文提出了一种新型混合智能模型 Attention-ResNet-LSTM，用于实时盾构机掘进速度（AR）的预测。针对盾构掘进过程中工况复杂、参数多变的特点，模型引入注意力机制，为不同输入赋予自适应权重。此外，该深度学习模型还包含 ResNet 和 LSTM 两个模块，能够充分提取掘进过程中的非线性空间和时序特征。本文以长江天然气管道项目的掘进数据为例，开展了模型性能验证。在实验前，对数据进行了提取、异常值检测与归一化预处理，并利用 EPR 算法筛选最优输入参数组合。随后，系统分析了序列长度、模型结构以及输入-输出相关性对模型性能的影响，并通过包含不同地层条件的案例研究，验证了模型在复杂地质环境下的适用性。最后，基于深圳白芒河隧道项目的独立数据库，检验了模型的泛化能力。主要结论如下：

(1) 通过 EPR 算法筛选，确定了刀盘转速（RS）、推进力（TH）、扭矩（TOR）、土体压缩模量（Es）和地基承载力特征值（BC）作为最优输入参数组合。其中，TH 与 TOR 与 AR 的相关性最强。不同作业参数对 AR 的预测值依赖性不同：当 RS 小于 0.7 r/min 时，AR 随 RS 略微减小，超过该值后 AR 随 RS 增大；TOR 与 TR 均与 AR 呈负相关关系，这与以往工程经验一致。

(2) 偏自相关函数分析结果表明，采用 20 min 的历史数据序列，能够在保证预测精度的同时，兼顾计算成本。同时，本文开展了参数化研究，探讨了 ResNet 层数与 LSTM 层数对模型性能的影响。结果显示，设置 2 层 ResNet 和 1 层 LSTM 可获得较优模型结构。预测结果与实测 AR 值拟合良好，且优于 ResNet-LSTM、LSTM、GRU 和 RNN 等其他智能模型。本模型在测试集上的 RMSE 和 MAPE 分别为 1.31 mm/min 和 1.53%，均优于对比模型。

(3) 在不同地层条件下，Attention-ResNet-LSTM 模型的预测性能优于 ResNet-LSTM。以同时包含硬黏土和软黏土的掘进案例为例，Attention-ResNet-LSTM 模型的 RMSE 为 2.52 mm/min，明显优于 ResNet-LSTM 的 2.79 mm/min。同时，本模型在泛化能力方面亦优于 ResNet-LSTM。当应用于不同项目数据库时，无论训练集中新增数据量多少，Attention-ResNet-LSTM 均能保持较高预测精度与稳健性；而 ResNet-LSTM 在完全缺乏先验数据的新项目中预测误差较大，易产生不可接受的误差。由此可见，Attention-ResNet-LSTM 能够根据掘进作业与地质条件自适应调整，而非仅适用于特定案例，这得益于注意力机制的引入。未来，随着更多不同隧道工程数据的积累，Attention-ResNet-LSTM 模型有望在新项目中实现更优预测表现。最终，随着输入-输出关系刻画精度不断提升，盾构机驾驶员可据此实时调整作业参数，保障掘进安全与效率。

竞争利益声明

作者声明本文不存在任何已知的潜在经济利益冲突或个人关系，这些情况可能会对本文所报告工作产生影响。

致谢

本研究得到了国家自然科学基金项目（资助编号：52008307）和上海市科技创新行动计划项目（资助编号：19DZ1201004）的资助。第三作者同时感谢中国博士后科学基金（资助编号：2023M732670）对本研究的支持。

附录 A. 补充数据

本文相关的补充数据可在线获取，网址：https://doi.org/10.1016/j.jrmge.2023.06.010。