【技术追踪】用于 CBCT 到 CT 合成的纹理保持扩散模型（MIA-2025）

  CBCT 到 CT 图像转译~

---

论文：Texture-preserving diffusion model for CBCT-to-CT synthesis
代码：https://github.com/zyj15416/TPDM-CBCT2CT

---

0、摘要

  锥形束计算机断层扫描（Cone Beam Computed Tomography, CBCT）作为一种重要的成像方式，在众多临床应用中发挥着关键作用，但其受到图像质量下降和噪声增加等固有局限性的制约。

  相比之下，计算机断层扫描（Computed Tomography, CT）能够提供更优的分辨率和组织对比度。因此，通过 CBCT 到 CT 的图像合成来弥合这两种成像方式之间的差距显得尤为迫切。（研究意义）

  深度学习技术已经提升了这种图像合成的效果，然而生成对抗网络（Generative Adversarial Networks, GANs）在应用中仍面临挑战。去噪扩散概率模型（Denoising Diffusion Probabilistic Models, DDPMs）作为一种新兴的图像合成技术，展现出了巨大的潜力。（生成模型简述）

  本文提出了一种新颖的纹理保持扩散模型，用于 CBCT 到 CT 的图像合成，该模型集成了自适应高频优化和双模式特征融合模块，旨在增强高频细节，有效融合跨模态特征，并保留精细的图像结构。

  广泛的验证表明，与现有方法相比，本文的方法具有更优越的性能，并展现出更好的泛化能力。所提出的模型为提高诊断准确性、优化治疗计划提供了一种变革性的途径，适用于各种临床场景。这项工作标志着在非侵入性、更安全且高质量的CBCT到CT合成领域迈出了关键一步，推动了个性化诊断成像实践的发展。（临床潜力）

---

1、引言

1.1、研究意义与当前挑战

  （1）CBCT 具有较低的辐射剂量且适用于局部解剖结构评估，但其图像质量欠佳、噪声水平较高以及有伪影存在；
  （2）在 CBCT 到 CT 合成中，生成对抗网络（GANs）仍然面临挑战，包括网络训练和在医学成像中的应用问题，可能导致不切实际的结构引入和复杂的训练；
  （3）尽管扩散模型在 CBCT 到 CT 合成中取得了成就，但在生成目标域的详细图像方面，尤其是在高频信息方面，仍存在不足；

1.2、本文贡献

  （1）提出了一种新的纹理保持扩散模型（texture-preserving diffusion model），专门用于 CBCT 到 CT 的合成，通过解决 CBCT 设备的局限性来提高 sCT 图像质量；
  （2）集成了一个自适应高频优化模块，该模块优先处理 CBCT 和 CT 分支中的高频细节，从而增强生成的 sCT 图像的质量和可解释性；
  （3）开发了一种基于 Transformer 的跨模态特征融合模块，采用注意力架构从显著区域启动 sCT 生成，并缓解潜在的合成问题；
  （4）在多中心验证中展现出比现有方法更优越的性能，证明了模型具有更强的泛化能力和鲁棒性；

---

2、方法

2.1、总览

  图 1 所示的方法采用了一个双分支的基于注意力机制的神经网络来对含噪 CT 图像进行去噪。该框架包含自适应高频优化（Adaptive High-Frequency Optimization, AHFO）模块、双模式特征融合（Dual-Mode Feature Fusion, DMFF）模块、时间嵌入（Time Embedded, TEB）模块以及一个边缘感知边界约束（Edge-Aware Boundary Constraint, EABC）损失函数，这些组件共同增强了传统的扩散范式，并提升了模型的特征提取能力。在去噪的同时，确保了与原始 CT 图像的一致性。

  在逆向扩散步骤中，条件分支整合了 CBCT 图像，以指导主 CT 生成分支中当前含噪 CT 图像的恢复过程。此外，一个可学习的高频优化模块在合成 CT 和 CBCT 特征中优化高频成分，其中在 CBCT 分支中使用快速傅里叶变换（Fast Fourier Transform, FFT），而在 sCT 分支中使用小波变换（Wavelet Transform, WT）。随后，DMFF 模块利用自注意力机制，有效地融合了两个分支的特征。

  在推理过程中，网络将从标准正态分布中采样的随机噪声与 CBCT 图像的输入相结合。这一过程最终生成了高质量的 sCT 图像，有效地实现了从 CBCT 到 sCT 的转换。总体而言，这种方法借助注意力机制、特征优化以及融合技术，对 CBCT 图像进行去噪，并生成高质量的 sCT 图像。

  
Figure 1 | 整体框架涵盖了正向和反向扩散过程： E1 和 D1 分别作为 sCT 生成主分支中的编码器和解码器；E0 用于引入额外的 CBCT 信息，而 D0 则是辅助解码器，用于引入边缘感知边界约束的额外损失函数；

2.2、自适应高频优化

  为了准确捕捉 CT 和 CBCT 图像中的高频细节，本文在频域中对提取的特征进行了优化。

  考虑到小波变换（WT）和快速傅里叶变换（FFT）的特点：小波变换在捕捉细粒度和局部频率结构方面特别有效，比快速傅里叶变换更为出色，因此在 CBCT 分支中应用了快速傅里叶变换，在 CT 生成分支中应用了小波变换，因为 CT 图像比 CBCT 图像具有更丰富的纹理特征。

  随后，通过变换函数 $\mathcal{F}$（WT 或 FFT）对输入特征图像 $x$ 进行分解，以获得子带特征图像 $X$，具体如下：

  为了优化提取的子带特征图像，重建 CT 图像的高频细节，并突出关键特征，引入了一个可学习的加权矩阵 $A$，具体如下：

  在此，$X^{\prime }$ 表示优化后的子带特征图像，$\odot$ 代表元素乘法。随后，通过逆变换函数 $\hat{\mathcal{F}}$，（IWT 或 IFFT），根据以下公式从优化后的子带特征图像中获得了最终输出 $X_{out}$：

2.3、双模式特征融合

  为了更有效地融合 CT 和 CBCT 分支的特征，提出了一种基于注意力机制的特征融合方法。具体而言，将通过自适应 WT 重建的 CT 分支特征图 hr 与经过 FFT 变换后得到的 CBCT 分支 条件特征 fr 进行融合。

  在该设计中，fr 作为生成查询（$Q$）和键值（$K$），而 hr 则用于值（$V$）的表示。通过重排方法，能够重构这些表示，并赋予它们多头注意力机制。

  为了计算注意力权重，首先根据公式（5）计算了向量 $Q$ 与 $K$ 之间的相似度，其中 $d$ 表示 $Q$ 和 $K$ 的维度。随后，对这个相似度矩阵应用了 SoftMax 函数，从而得到了归一化的注意力权重：

  这些权重突出了 CT 特征图上与 CBCT 特征图每个位置相关联的区域。随后，利用这些注意力权重对 $V$ 进行优化，从而根据源自 CBCT 的注意力分数，聚合 CT 和 CBCT 特征图的信息：

  生成的聚合输出经过 batch 归一化（BN）和残差块（ResBlock）处理，最终得到融合特征图。随后，通过应用自注意力层进一步突出融合后的关键区域。

2.4、时间嵌入模块

  在正向扩散过程中，基于马尔可夫链，通过在每一步添加不同程度的噪声来模拟数据的扩散过程。为了在逆向扩散过程中准确捕捉不同时间步的噪声特征，在扩散模型的 E1 编码器和 D1 解码器中引入了一个关键组件——时间嵌入模块。（嘶，步长 $t$ 嵌入不是标配的么）

  具体而言，将来自不同时间步的信号输入到一个多层感知器（MLP）层，该层由四个部分组成：一个嵌入层、两个线性（全连接）层和一个 GELU 激活层。最初，时间信息通过嵌入层使用正弦位置编码进行处理，其公式如下：

  其中，$t$ 表示时间步长，$i$ 表示维度索引，$TE(t,i)$ 表示第 $i$ 个索引在时间步长 $t$ 时的编码值，而 $\lambda$ 作为幅度值。在这个公式中 $\lambda$ 是一个超参数，用于调整时间编码的频率，影响正弦和余弦函数的周期，从而影响时间编码的特性。

  $d_{model}$ 表示时间编码输出的维度大小。经过时间编码后，通过两个全连接层和一个 GELU 激活层对增强的时间信息 $t^{\prime }$ 进行处理。随后，$t^{\prime }$ 沿特征维度被分为两部分：尺度和偏移量。

  这些组件可以动态调整模型的输出特征，显著提高其处理不同时间步长固有动态噪声的能力，并最终在 CBCT 到 CT 合成中表现出色。

2.5、损失函数

2.5.1、边缘感知边界约束

  为了更好地捕捉轮廓内部的细节，并减少除 CT 细节之外的背景信息的干扰，如 图 1 所示，引入了一个辅助解码器 D0 作为第二个输出，以精确预测一幅清晰的 CT 图像。通过在 D0 的输出与原始 CT 图像之间应用基于梯度的拉普拉斯边界提取方法，实现了梯度边界约束损失函数。

  在此，利用拉普拉斯算子计算了 D0 解码器的输出 $I_{D_0}$ 在每个像素点 $(x,y)$ 处的二阶梯度 ${\nabla }^2{I}_{D_0}(x,y)$：

  此外，通过二值化处理来增强边缘的表示：

  其中，$\theta$ 是一个预设的阈值，用于调整边缘的丰富度。本文经验性地将 $\theta$ 设定为0.1。通过这种方法，得到了一个清晰的边缘图 $B(x,y)$，其中 “1” 表示边缘像素，“0” 表示非边缘像素。同样，原始 CT 图像的二阶梯度信息 $P(x,y)$ 被计算出来，作为 EABC 损失函数 ${\mathcal{L}}_{EABC}$：

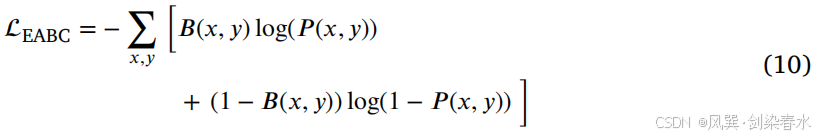
  在这个损失函数中，$B(x,y)log(P(x,y))$ 衡量了当实际值为 1（边）时的预测误差；而$(1-B(x,y))log(1-P(x,y))$ 则衡量了当实际值为 0（非边）时的预测误差。

2.5.2、总损失

  在本研究中，除了 EABC 之外，还需要使用两种额外的损失函数，即 ${\mathcal{L}}_1$ 和 MSE 损失。利用扩散模型的主要解码器 D1 来预测噪声，并通过在每一步中减去预测的噪声来获得优化的 CT 图像。在每一步中，MSE 损失的表达式为：

  $N$ 表示一批中的样本数量，$ou{t}_{D1}^j$ 代表第 $j$ 个样本的 D1 输出，而 ${\epsilon }_{gt}^j$ 则是在前向扩散过程的相应步骤中添加到第 $j$ 个样本的噪声。此外，为了应对 CT 图像中的潜在异常值，采用了以下 ${\mathcal{L}}_{L_1}$ 损失函数：

  其中，$N$ 表示批次样本量，$ou{t}_{D0}^j$ 代表第 $j$ 个样本的 D0 输出，而 $X_{CT}^j$ 则指该批次样本中原有的第 $j$ 个 CT 图像。总损失函数的公式如下：

  在这里，$\alpha$ 表示每个损失的系数，反映了该损失在总体损失计算中的相对重要性。在本研究中，设定了 ${\alpha }_{EABC}=10^{-3}$，${\alpha }_{MSE}={\alpha }_{L_1}=1$ 。

2.6、加速推理

  原文略，DDIM 采样：

---

3、实验与结果

3.1、数据集

  （1）内部骨盆数据集：79名患者，8:1:1 划分，训练集包含 5056 个切片，验证集包含 561 个切片，测试集则包含 624 个切片；

  （2）外部骨盆数据集：公开数据 Pelvic Reference Data；

  （3）不同部位的大脑数据：SynthRAD2023 挑战数据集的头部数据集；

3.2、数据配准

  采用了先进的非线性配准技术——对称归一化（SyN），将 CBCT 图像（作为移动图像）映射到 CT 图像（作为固定对照）上，完成配准。

3.3、评价方法

  （1）对比模型：U-Net，Pix2Pix，CycleGAN，EaGANs，ResViT，CDDPM，DDMM，SynDiff，FGDM；

  （2）评价指标：RMSE，SSIM，PSNR；

3.4、实施细节

  （1）图像大小：256×256；
  （2）batch size为32，AdamW 优化器；
  （3）总扩散步数1000 步，推理采样60步内完成；
  （4）余弦退火策略调整学习率；
  （5）自动混合精度；

3.5、内部骨盆数据集的实验结果

  
Table 1 | 内部骨盆测试数据集的实验结果：

  
Figure 2 | 内部骨盆测试数据集可视化：这里选取了三个典型案例：一个来自健康个体；一个来自患有子宫肌瘤的个体，用红色虚线椭圆标出；另一个来自髋关节植入金属假体的个体。（A1-J1）、（A2-J2）和（A3-J3）分别是 CT 图像与相应预测 sCT 图像之间的绝对差异。CBCT 的显示范围为 [−800,−50] HU，而 CT 和 sCT 的显示范围则为 [−160,240] HU;

  
Figure 3 | 图2 所示的一维强度分布是通过沿红色虚线扫描得到的：图中的插图清楚地显示了与其它方法相比，所提出的方法具有优越的性能:

3.6、外部骨盆数据集的实验结果

  
Table 2 | 外部骨盆测试数据集的实验结果：

  
Figure 4 | 外部骨盆测试数据集可视化：（A1-J1）和（A2-J2）是 CT 与相应预测的 sCT 之间的绝对差异图像，CBCT 的显示窗口在外部测试数据集中为 [−750,250] HU，而 CT 和 sCT 的显示窗口则为 [−160,240] HU；

3.7、头部数据集的泛化性

  
Table 3 | 头部测试数据集的实验结果：

  
Figure 5 | 头部测试数据集可视化：第二行和第四行显示了红色虚线框标记的放大区域，定量结果位于预测图像底部，CBCT 的显示窗口范围为 [−1000,340] HU，而 CT 和 sCT 的显示窗口则为 [−160,240] HU；

3.8、消融实验

  
Table 4 | 对所提出的生成器进行了消融研究，其中，Vanilla 指的是原始模型，而 modified 则是指使用开发的生成器替换原有的生成器：

  
Table 5 | 与各种改良模型的比较，用于消融研究：

  
Table 6 | WT 和 FFT 之间选择的消融研究：

  
Figure 6 | 网络训练过程中对验证数据集的评估结果：

  
Figure 7 | 不同程度的噪声对模型鲁棒性的影响：

---

  嘶，在频域搞操作真有效么(●’◡’●)