3.3.2 纠错编码（海明校验码）

在这一小节中，我们会继续探讨海明校验码，海明校验码又可以称为汉明教验码，这只是一个音译的问题，因为发明这个校验码的人叫理查德 汉明，也正是因为发明了海明码，对于信息纠错这个领域的贡献十分巨大，所以这个人获得了1968年的图灵奖。这一小节中，我们会首先介绍海明码的基本实现思想，然后再来介绍怎么构建海明码、怎么使用海明码来进行校验。

首先我们从奇偶校验出发，这种校验的思想很简单，对于n个有效的信息位，我们只需要在首部或者尾部添加一个奇校验位或者偶校验位，用这样的方式构成奇偶校验码。比如对于偶校验来说，四个信息位1010，我们需要在头部添加一个零保证整体来看总共有偶数个1。奇偶校验码的一个局限性就是我们只能发现奇数位的错误，并且我们知道它错了，但是我们无法确定是哪一位出了错，所以当我们发现错误的时候，我们没办法自动的把它进行修正，只能要求数据的传输方重新传送。可以这么来理解：由于奇偶校验的策略，我们只添加了一个校验位，也就是一个比特的信息，而一个比特的冗余信息，显然它只能携带两种状态，也就是只能反馈对或者错这样的两种状态。

而这一小节我们要学习的海明码，其实是基于偶校验的一个拓展。大致的思路是这样的：对于n个有效的信息位，我们会把它分为k个分组，然后对k个分组分别的进行偶校验，也就是说，每一个分组会对应一个校验位，最终我们会携带k个校验位，而这 k 个校验位显然可以反映更多种状态的信息。除了反馈对错之外，我们甚至还可以知道错在哪儿，是哪一位出了错，这就是海明码的设计思想。基于这个思路，我们接下来要探讨两个问题，第一个问题，我们需要把这n个信息位分为多少个分组呢？第二个问题，这n个信息位我们应该怎么把它们分派到各个分组当中。

首先我们来探讨第一个问题，需要设置多少个校验位？我们假设信息位总共有n个，然后我们添加的冗余校验位有k个，现在我们所期待的效果是k个校验位除了能反映对错之外，还能指明我们到底是哪一个比特位出现了错误，显然k个比特总共能表示二的k次方这么多种状态。而我们的海明校验码整体来看，应该是信息位加校验位，总共n+k这么多位。也就是说，这 n+k 个位都有可能会出错，所以这二的 k 次方这种状态当中。显然需要包含 n+k 种情况，那除了出错的这 n+k 种情况之外，还需要包含一种正确的状态，因此我们可以得到这样的一个不等式，2的k次方，应该要大于等于n+k+1。对于这个不等式背后的逻辑，现在理解的不是很清楚也没有关系，同学们只需要把它记住，能够用出来就可以了，总之我们需要通过这个不等式来确定我们需要添加多少个校验位，比如如果有四个信息位，那么我们就只能取k=3才能满足这个式子。因为如果 k=2 的话，那么二的二次方等于四，然后右边是四+2+1 是不满足大于等于这个条件的。因此，对于四个信息位，我们至少需要添加三个校验位，也就是把这些信息位分为三个分组。最下面这张表给出了n和k的一个对应关系，大家可以简单的看一下，当然了，考试的时候临时推也不难。只需要把k带几个值进去算一下就知道了。

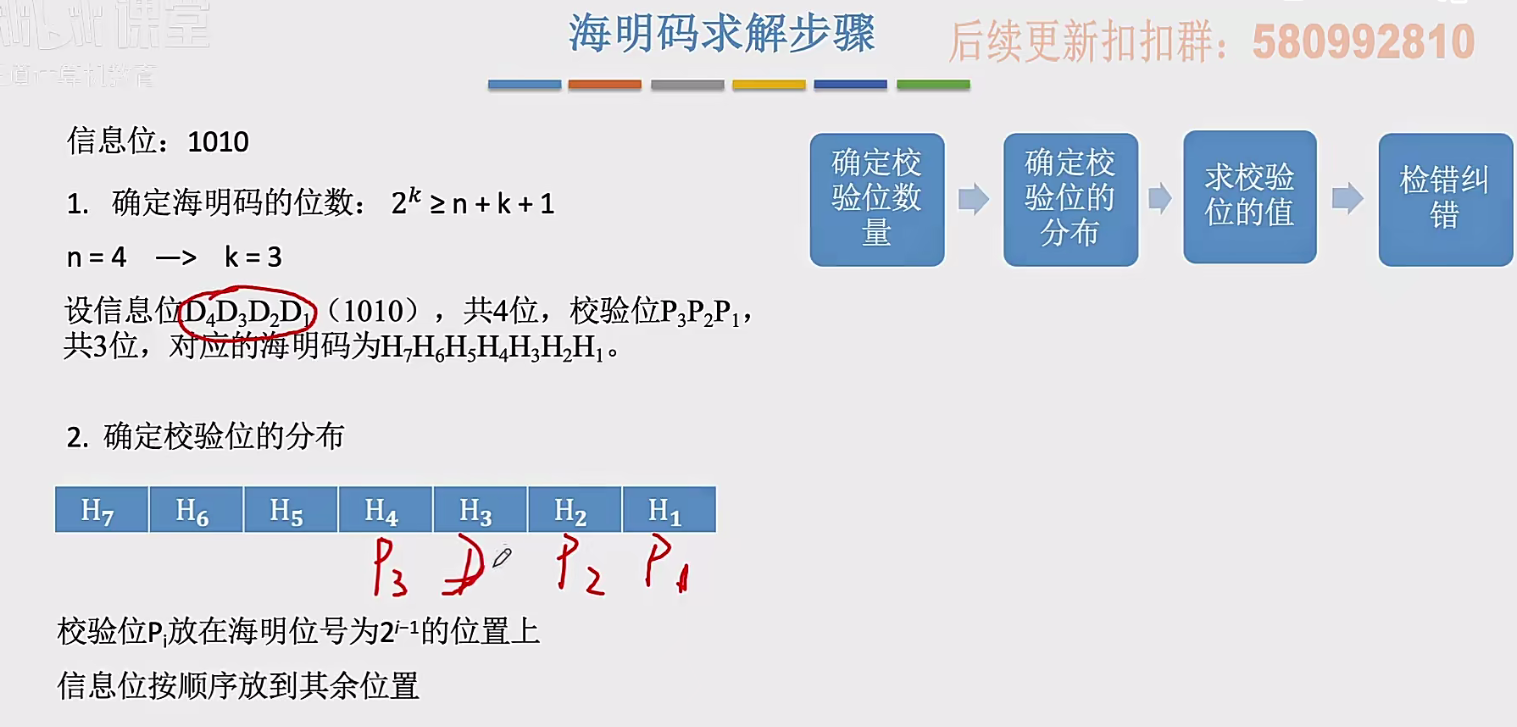
基于刚才的结论，如果说有四个信息位的话，那么我们可以确定我们要添加的校验位的数量k=3，也就说最终我们生成的海明校验码应该是四位再加三位，总共七位这么多。为了区分信息位和校验位，我们用D1到D4来表示这四个信息位，然后用P1到P3来表示这三个校验位，然后用H1到H7来分别对应最终的这七位海明码。那这些信息位和校验位应该放到什么位置呢？一个很容易想到的办法是把这三个校验位放到头部的位置，然后把四个信息位放到尾部的位置。但是海明码不能这么
做，它有一些特殊的规定。在海明校验码中，我们规定所有的这些校验位应该放在二的i-1次方这些位置上，也就是说P1、P2、P3这几个校验位，我们应该分别把它们放到一、二、四这几个位置，那如果还有一个校验位P4的话，显然应该放到八。有没有发现规律，其实和我们二进制的一个权值的上升关系是相符合的：一、二、四、八、十六。所以我们可以把这些校验位它所放的位置看作是这个校验位它所对应的某一种权值，那这个权值有什么用？我们一会儿再来解释。总之P1放到一的位置，P2放到二这个位置，P3 要放到四这个位置，剩下的这些位置我们再把它填入各个信息位。哪有空就填到哪，D1放到H3，D2、D3、D4。

就是这样的一个分布关系。目前为止，我们已经确定了我们需要添加三个校验位，或者换一个角度来说就是需要把这些信息位分为三个分组，然后每个分组分别进行偶校验。因此接下来我们应该确定一种规则，就是三个分组当中，应该分别包含哪几个信息位？当我们确定了如何分组之后，那么与这个分组相对应的偶校验位的值是不是就很好确定了？

来看一下怎么做，我们需要把这些信息位所处的位置这个序号用二进制的方式把它表示出来，比如说对于D1这个信息位来说，它所处的位置是三，那么三的二进制表示应该是011，下一个信息位是D2，它所处的位置是五，那么五用二进制表示应该是101，D3所处的位置是六，六用二进制表示应该是110，最后是D4，它处于七这个位置，用二进制表示就是111。之前我们说过P1、P2、P3 分别把它放到一、二、四这些位置，我们可以把它理解为某一种权重。那么这些权重和刚才我们提到的这三个二进制数的权重是一一对应的，所以P1 这个偶校验位，它所属的分组当中应该有哪些信息位呢？我们只需要把末位为1的这几个信息位，把它归为P1所属的分组就可以了，也就是 H3、H5、H7 这几个位置所对应的信息位归为同一个分组进行偶校验，只需要把这个组里边的所有信息位进行异或运算，就可以确定我们的P1应该取0还是取1，这就是P1的计算方式。

接下来第二个分组我们应该让它包含H3、H6和H7所对应的这几个信息位，也就是D1、D3和D4，把这几个信息位进行异或运算所得到的结果就应该是这个分组的偶校验位的一个值。最后一个分组的确定方法也是一样的，H5、H6和H7也就是D2、D3、D4，它们属于同一个分组，把它们异或可以得到偶校验位的值。所以对于第一个分组D1、D2、D4，也就是011分别进行异或。首先是D1和D2的异或是等于1，然后这个1再和D4进行异或是等于0，所以P1的值我们就确定了，应该是等于0。换个角度来说，就是这个分组当中信息位加上校验位，总共只有偶数个1。
接下来对于第二个和第三个分组的偶校验原理，其实也是类似的，就不再赘述，基础不好的同学可以暂停下来理解一下。到目前为止，我们已经确定了P1、P2、P3的值，应该分别是010，我们就确定了整个海明校验码的一个值，应该是这样的一个状态。接下来我们就可以利用这个海明码来进行检错和纠错，怎么检测出错误呢？其实就是把各个分组内的这些二进制比特位，进行一个异或运算，也就是对各个分组进行偶校验，如果说这个分组内没有出错的话，那么进行异或运算得到的结
果应该是零。

具体看一下，如果现在接收方接收到的数据没有发生任何一个比特位的错误，大家可以暂停来自己验证一下。我们根据刚才确定的这三个分组，对每个分组内的这些比特位依次进行异或运算，因为每个分组都有偶数个1，所以异或之后肯定都是000，这是没有出错的情况，再来看一个出错的情况，如果说接收方接收到的数据H2这一位发生了错误，也就是P2这个校验位，从1变成了0，那么第一个分组进行异或得到0，第二个分组中由于P2发生了跳变，所以导致第二个分组中，现在只有奇数个1，那么异或出来的结果就是1。第三个分组也是一样的。没有任何一个数据发生跳变，因此异或的结果应该是0，现在我们根据S1到S3这几个位就可以确定应该是010这个位出现了错误，那010转换成十进制不就是二吗？也就是说S3、S2、S1所组成的这个二进制数指明了我们出错的位置到底在哪。如果我们求得的值，比如说110的话，那么就说明出错的位置应该是在六这个位置，
因为110转换成十进制是六。这就是使用海明码进行纠错的一个过程，是不是觉得很神奇？

给大家一个图，你就能理解为什么能呈现出这样的规律了。这个图里边每一个圆圈表示的是从属于同一个分组的比特位。P1、D1、D2、D4从属于同一个分组，P2、D1、D4从属于第二个分组，P3、D2、D3、D4从属于第三个分组，而这三个分组相互之间是有交集的。所以来看一下，如果说D3这个信息位发生了跳变，由于第二个分组和第三个分组都包含了D3这个信息位。因此，D3的跳变会导致S2和S3算出来的结果都是1。而S1当中所有的这些信息位都没有跳变，因此它算出来的结果肯定是0。那么我们最终得到的S3到S1结果不就是110吗，也就是6，刚好就指向了D3所对应的位置。再看之前这个例子，我们是假定了P2发生了跳变，那么P2它只从属于第二个分组，因此它只会影响S2的值，而我们得到的结果101刚好又是指向了P所处的位置H2，再来一个例子，如果说是D4发生了跳变。那么你看一下D4它从属于所有的这些分组，因此所有的分组的偶校验，或者说这个异或运算的结果肯定都会被影响为1，而三个1对应的十进制不刚好就是七吗，同样也是指向了D4它所处的这个位置。这就是海明码的一个纠错原理，大家可以再结合这个图好好体会一下。

接下来要补充一些大家做题的时候可能会遇到的情况，有的题目当中对于信息位校验位的一个编号，可能是从小到大这么编的，而我们刚才讲的是从大到小，那对于这种题目，其实做法是一模一样的，只不过是左右方向换了而已，题目的做法上没有任何区别。

另外一个要补充的点是海明码具有一个比特位的纠错能力，还有两个比特位的检错能力，但是如果使用之前我们提出的这个方案的话。其实，在检错和纠错的时候，有可能会发生一些问题。来看这样的一个例子，假设我们在传输的过程当中得到的这串海明码P1和P2。这两个位发生了跳变，那么得到的结果就是S1=1，S2=1，S3=0。那么按照我们之前定下的规则，011对应的十进制是三，那这是否说明了H3这个位置出现了错误呢？显然，这个结论是不对的。

此时我们是发生了两个比特位的跳变，也就是说，基于之前提出的方案，我们是没有办法区分到底是一个比特位的错误，还是两个比特位的错误？所以为了解决这个问题，实际海明码在使用的时候通常还会在最首部加上一个全校验位。所谓全校验，就是对我们之前得到的这一整体全部的这些比特信息统一的进行一次偶校验，所以看一下之前这些例子当中总共有一个两个三个一，所以这个全校验位我们应该把它设为1，保证整体来看有偶数个1。添加了这个全校验位之后呃=，如果我们求得的S1到S3全部是0，并且全体的偶校验是成功的，那么就说明此时没有发生错误，而如果S1到 S3不等于0，并且全体的偶校验失败，说明有一位的错误，我们只需要把它纠正就可以，比如P1 发生了跳变，最终我们S1到S3应该是001，也就是指向了1这个位置，而由于只有P1这样一个位发生了跳变，就导致整体的偶校验是失败的。这个时候就说明H1这个位发生了错误，我们只需要把它从1改为0就可以，不需要要求发送方重新发送这个数据。再来看，如果说有两个位发生了错误，就像刚才那个例子一样P1、P2同时发生了错误，那么S1到S3得到的结果应该是零一一。但这种情况下，整体的偶校验是会成功的，所以此时就说明是发生了两个比特位的错误。由于我们没有办法确定这两个比特位错在哪，所以我们就需要要求对方重新传送这些数据。

一小节中我们学习了海明校验码，在所有的数据校验方式当中，海明码是比较难理解的，但是如果我们从它的基本思想出发，就能更方便的理解为什么海明码要这么设计。本质上，它就是把所有的信息位进行分组，然后每一个组都进行偶校验，而每一个分组会对应一个校验位，所以如果有k个分组的话，自然就会有 k 个校验位。对于海明码的求解，我们首先需要确定校验位的位数。接下来需要确定各个校验位，还有信息位的分布，所有的这些校验位应该是分布在编号为一二四八
十六这些个位置。我们可以把这些校验位的位置信息理解为某一种权重，这些权重信息可以帮助我们记忆和理解，当我们在进行分组的时候，这个分组规则是怎么制定的？每一个校验位所属的分组，都应该确保它们拥有偶数个1。在进行减错纠错的时候，我们就可以根据各个分组是否满足拥有偶数个1这样的一个条件来判断哪些分组出现了问题，根据各个分组偶校验的一个结果，我们就可以来判断到底是哪个位置出现了错误。
在这个小节的最后，我们也补充了海明码的一个纠错和减错能力。只不过为了区分到底是一位错还是两位错，我们通常还会在最高位加上一个全校验位，保证海绵码的整体有偶数
个1。

以上就是这小节的全部内容。