循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释)
我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的),根据CRC编码的规则,得到编码后的消息 T T T,将该“加密”后的消息 T T T 发送给接收方,接收方能够根据 T T T,检验发送消息的过程中是否出现了错误。
算法步骤:
- 将 k k k 位信息写成 k − 1 k-1 k−1 阶多项式 M ( x ) M(x) M(x)
- 设生成多项式 G ( x ) G(x) G(x)的阶为 r r r
- 用模2除法计算 x r M ( x ) / G ( x ) x^rM(x)/G(x) xrM(x)/G(x) ,获得余数多项式 R ( x ) R(x) R(x)
- 用模2减法球的传送多项式 T ( x ) T(x) T(x), T ( x ) = x r M ( x ) − R ( x ) T(x)=x^rM(x)-R(x) T(x)=xrM(x)−R(x),则 T ( x ) T(x) T(x) 多项式系数序列的前 k k k位位信息位,后 r r r位为校验位,总位数 n = k + r n=k+r n=k+r
- 接收方解码方法:将 T ( x ) T(x) T(x) 除以 G ( x ) G(x) G(x) ,得到一个属,如果这个余数为0,则说明传输中无错误发生,否则说明传输有误。
(算法步骤没看明白没有关系,都是看示例想清楚的,看下面给出示例就好~)
CRC计算示例:
题目描述:待发送的信息为1001,生成多项式为G(x)=1011,计算余数R(x),传递的信息T(x),展示循环冗余校验的过程。
生成多项式 G ( x ) = 1011 G(x)=1011 G(x)=1011,对应的阶为 r = 3 r=3 r=3 (总位数-1),
将原始待发送的信息 M ( x ) M(x) M(x)左移 r = 3 r=3 r=3 位,得到 M ( x ) ′ = 1001000 M(x)'=1001000 M(x)′=1001000(右侧补3个0),
用左移后的 M ( x ) ′ M(x)' M(x)′除以给定的生成多项式 G ( x ) G(x) G(x),
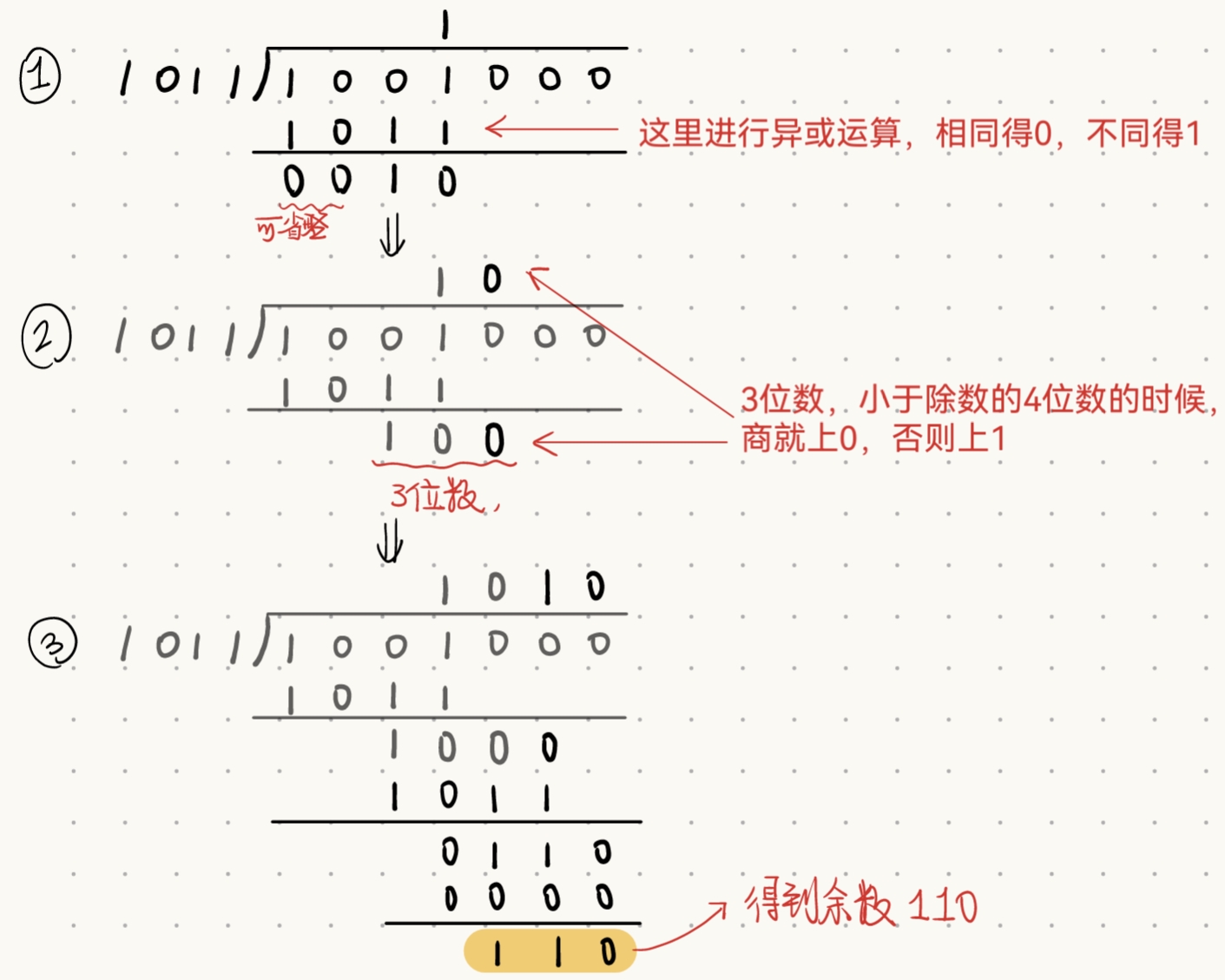
运算结果得到余数 R ( x ) = 110 R(x)=110 R(x)=110,
将待发送信息 M ( x ) M(x) M(x) 左移后的信息加上得到的余数 R ( x ) R(x) R(x),就得到应传送的信息
T ( x ) = 1001000 + 110 = 1001110 T(x)=1001000+110=1001110 T(x)=1001000+110=1001110,
发送码即为 1001110 1001110 1001110,其中前4位为原始发送信息为 1001 1001 1001,后3位为校验位 110 110 110。
- ( M(x) = 1001 )(信息码:9)
- ( G(x) = 1011 )(生成多项式:( x^3 + x + 1 ))
- 余数 ( R(x) = 110 ) → 发送码:1001110
接收方校验过程:
若接受到的消息为 1000110 1000110 1000110,用该数除以 G ( x ) G(x) G(x)(除法规则与上述相同),得到余数为 000 000 000,说明接受到的消息正确✔。
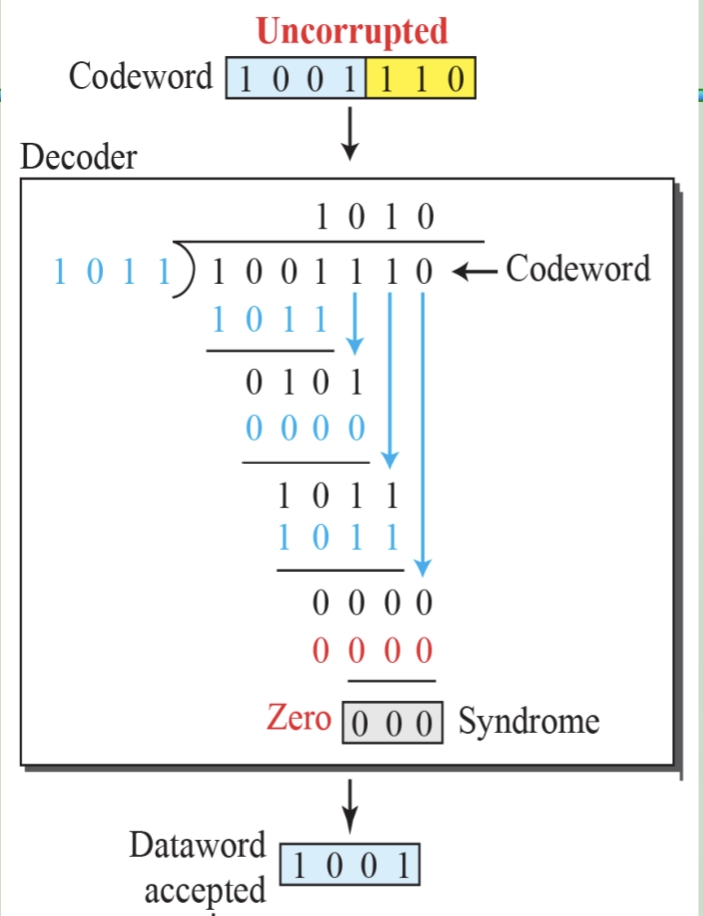
若接收到的信息为: 1001110 1001110 1001110,用该数除以 G ( x ) G(x) G(x)(除法规则与上述相同),得到余数为 011 011 011,余数不为0,说明接受到的消息错误❌。

