matlab自控仿真【第一弹】❀传递函数和输出时域表达式
内容
- 入门语法知识
- 一、传递函数模型建立
- 1. `tf()`:有理分式模型(多项式形式)
- 2. `zpk()`:零极点增益模型
- 3. 系统连接函数:`series()`, `parallel()`, `feedback()`
- 二、系统稳定性分析
- **1. `pzmap()`:绘制零极点图
- 2. `roots()`:求极点(特征根)
- 三、时域响应分析
- 1. `gensig()`:生成特定激励信号
- 2. `lsim()`:任意输入的响应
- 3. `impulse()`:冲激响应
- 4. `step()`:阶跃响应
- 总结练习:完整案例
- 案例
- 小贴士
入门语法知识
以下是针对每个函数和命令的详细使用说明及示例代码,帮助你逐步掌握MATLAB在控制系统分析中的应用:
一、传递函数模型建立
1. tf():有理分式模型(多项式形式)
功能:用分子/分母多项式的系数向量创建传递函数。
语法:sys = tf(num, den)
num:分子多项式系数(降幂排列,缺项补0)。den:分母多项式系数(降幂排列,缺项补0)。
示例1:一阶系统
创建传递函数 ( G(s) = \frac{1}{T s + 1} )(( T=0.5 )):
T = 0.5;
num = [1]; % 分子系数 [1]
den = [T, 1]; % 分母系数 [0.5, 1]
sys_tf = tf(num, den);
disp('一阶系统传递函数:');
sys_tf

示例2:二阶系统
创建传递函数 ( G(s) = \frac{\omega_n2}{s2 + 2\zeta\omega_n s + \omega_n^2} )(( \zeta=0.7, \omega_n=5 )):
zeta = 0.7;
wn = 5;
num = [wn^2]; % 分子系数 [25]
den = [1, 2*zeta*wn, wn^2]; % 分母系数 [1, 7, 25]
sys_tf = tf(num, den);
disp('二阶系统传递函数:');
sys_tf

2. zpk():零极点增益模型
功能:用零极点和增益创建传递函数 ( G(s) = K \frac{(s-z1)(s-z2)…}{(s-p1)(s-p2)…} )。
语法:sys = zpk(z, p, K)
z:零点向量(列向量或行向量)。p:极点向量。K:增益常数。
示例:创建零极点模型 ( G(s) = 5 \frac{s+2}{(s+1)(s^2+4s+8)} ):
z = [-2]; % 零点:s=-2
p = [-1, -2+2i, -2-2i]; % 极点:s=-1, s=-2±2i
K = 5; % 增益
sys_zpk = zpk(z, p, K);
disp('零极点增益模型:');
sys_zpk

3. 系统连接函数:series(), parallel(), feedback()
功能:
series(sys1, sys2):串联系统 ( G(s) = G1(s) \cdot G2(s) )。parallel(sys1, sys2):并联系统 ( G(s) = G1(s) + G2(s) )。feedback(sys1, sys2, sign):反馈连接 ( G(s) = \frac{G1(s)}{1 \pm G1(s)G2(s)} )(sign默认+1,负反馈用-1)。
示例:
% 定义子系统
sys1 = tf([1], [1, 2]); % G1(s) = 1/(s+2)
sys2 = tf([3], [1, 1]); % G2(s) = 3/(s+1)% 串联
sys_series = series(sys1, sys2);
disp('串联后的传递函数:');
sys_series% 并联
sys_parallel = parallel(sys1, sys2);
disp('并联后的传递函数:');
sys_parallel% 负反馈(单位反馈)
sys_feedback = feedback(sys1, 1); % 等价于 feedback(sys1, sys2=1, -1)
disp('负反馈后的传递函数:');
sys_feedback


二、系统稳定性分析
**1. pzmap():绘制零极点图
功能:显示传递函数的零点(o)和极点(x)在复平面的位置。
语法:
pzmap(sys):绘制系统sys的零极点图。[z, p] = pzmap(sys):返回零点和极点坐标。
示例:绘制二阶系统 ( G(s) = \frac{25}{s^2 + 7s + 25} ) 的零极点图:
zeta = 0.7;
wn = 5;
sys = tf([wn^2], [1, 2*zeta*wn, wn^2]);
pzmap(sys);
title('二阶系统零极点图');
grid on;

2. roots():求极点(特征根)
功能:计算分母多项式的根(即系统极点),判断稳定性(所有极点在左半复平面则稳定)。
语法:poles = roots(den)
den:分母多项式系数向量。
示例:求 ( s^2 + 4s + 3 = 0 ) 的根:
den = [1, 4, 3];
poles = roots(den);
disp('极点位置:');
poles

稳定性判断:
- 若所有极点实部 < 0:系统稳定。
- 若有极点实部 = 0:临界稳定(如纯虚根)。
- 若有极点实部 > 0:不稳定。
三、时域响应分析
1. gensig():生成特定激励信号
功能:生成正弦波、方波等信号。
语法:[t, u] = gensig(type, freq, len, dt)
type:信号类型('sin'或'square')。freq:频率(Hz)。len:信号持续时间(周期数,对正弦波)或总时长(秒,对方波)。dt:采样时间间隔。
示例:生成频率1Hz、时长5秒的方波:
[t, u] = gensig('square', 1, 5, 0.01); % dt=0.01s
plot(t, u);
title('方波信号');
xlabel('时间 (s)');
ylabel('幅度');


2. lsim():任意输入的响应
功能:计算系统对任意输入信号的响应。
语法:y = lsim(sys, u, t)
sys:系统模型(tf或zpk对象)。u:输入信号向量。t:时间向量。
示例:用方波激励一阶系统 ( G(s) = \frac{1}{0.5s+1} ):
% 定义系统
sys = tf([1], [0.5, 1]);% 生成方波信号
[t, u] = gensig('square', 0.5, 10, 0.01); % 频率0.5Hz,时长10s% 计算响应
y = lsim(sys, u, t);% 绘图
plot(t, u, 'r--', t, y, 'b-');
title('一阶系统对方波的响应');
xlabel('时间 (s)');
ylabel('幅度');
legend('输入信号', '系统响应');
grid on;

3. impulse():冲激响应
功能:计算系统的单位冲激响应。
语法:
impulse(sys):直接绘图。[y, t] = impulse(sys):返回响应数据。
示例:绘制二阶系统的冲激响应:
sys = tf([4], [1, 3, 2]); % G(s)=4/(s²+3s+2)
impulse(sys);
title('二阶系统冲激响应');
grid on;

4. step():阶跃响应
功能:计算系统的单位阶跃响应。
语法:
step(sys):直接绘图。[y, t] = step(sys):返回响应数据。
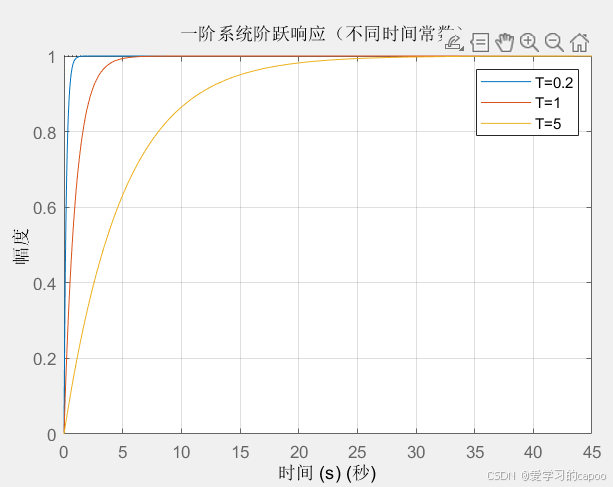
示例:绘制一阶系统不同时间常数的阶跃响应对比:
T1 = 0.2; T2 = 1; T3 = 5; % 时间常数
sys1 = tf([1], [T1, 1]);
sys2 = tf([1], [T2, 1]);
sys3 = tf([1], [T3, 1]);step(sys1, sys2, sys3);
title('一阶系统阶跃响应(不同时间常数)');
xlabel('时间 (s)');
ylabel('幅度');
legend(['T=', num2str(T1)], ['T=', num2str(T2)], ['T=', num2str(T3)]);
grid on;
总结练习:完整案例
目标:分析二阶系统 ( G(s) = \frac{100}{s^2 + 10s + 100} ) 的稳定性和阶跃响应。
% 1. 创建传递函数模型
num = [100];
den = [1, 10, 100];
sys = tf(num, den);% 2. 稳定性分析
poles = roots(den); % 求极点
disp('极点位置:');
disp(poles);
disp('稳定性判断:');
if all(real(poles) < 0)disp('系统稳定');
elsedisp('系统不稳定');
end% 3. 绘制零极点图
pzmap(sys);
title('二阶系统零极点图');
grid on;% 4. 绘制阶跃响应
step(sys);
title('二阶系统阶跃响应');
grid on;
通过以上示例,你可以逐步掌握每个函数的用法。建议从简单系统开始,修改参数观察结果变化,加深对控制系统原理的理解。
案例


小贴士
1.注意
多打几遍就好了,加油ヾ(◍°∇°◍)ノ゙
