向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的对称与统一。本文将从叉乘模长的本质出发,延伸至内积与投影的深层关系,最终探索两者在几何与代数层面的内在一致性。

叉乘模长:空间张量与方向正交性的度量
叉乘运算 a × b \mathbf{a} \times \mathbf{b} a×b 定义了一个全新的向量,其方向垂直于原始向量 a \mathbf{a} a 和 b \mathbf{b} b 所确定的平面,遵循右手定则。这一运算的核心价值不仅在于方向性,更在于其模长的几何意义:

∣ a × b ∣ = ∣ a ∣ ∣ b ∣ sin θ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin \theta ∣a×b∣=∣a∣∣b∣sinθ
其中 θ ∈ [ 0 , π ] \theta \in [0, \pi] θ∈[0,π] 为两向量间的夹角。该公式揭示了一个深刻的几何事实——叉乘的模长等于以 a \mathbf{a} a 和 b \mathbf{b} b 为邻边的平行四边形的面积。这意味着叉乘模长本质上是向量对平面空间的“张量能力”的量化:当两向量垂直时 ( θ = π / 2 \theta = \pi/2 θ=π/2),面积最大;当它们平行时 ( θ = 0 \theta = 0 θ=0),面积坍缩为零。

坐标框架下的验证:代数的严谨性
在三维笛卡尔坐标系中,设 a = ( a 1 , a 2 , a 3 ) \mathbf{a} = (a_1, a_2, a_3) a=(a1,a2,a3), b = ( b 1 , b 2 , b 3 ) \mathbf{b} = (b_1, b_2, b_3) b=(b1,b2,b3),叉乘结果为:
a × b = ( a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ) \mathbf{a} \times \mathbf{b} = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1) a×b=(a2b3−a3b2,a3b1−a1b3,a1b2−a2b1)
其模长为:
( a 2 b 3 − a 3 b 2 ) 2 + ( a 3 b 1 − a 1 b 3 ) 2 + ( a 1 b 2 − a 2 b 1 ) 2 \sqrt{(a_2b_3 - a_3b_2)^2 + (a_3b_1 - a_1b_3)^2 + (a_1b_2 - a_2b_1)^2} (a2b3−a3b2)2+(a3b1−a1b3)2+(a1b2−a2b1)2
通过展开并与 ∣ a ∣ 2 ∣ b ∣ 2 sin 2 θ = ∣ a ∣ 2 ∣ b ∣ 2 − ( a ⋅ b ) 2 |\mathbf{a}|^2|\mathbf{b}|^2 \sin^2 \theta = |\mathbf{a}|^2|\mathbf{b}|^2 - (\mathbf{a} \cdot \mathbf{b})^2 ∣a∣2∣b∣2sin2θ=∣a∣2∣b∣2−(a⋅b)2 对比,可严格证明该表达式等价于 ∣ a ∣ ∣ b ∣ sin θ |\mathbf{a}||\mathbf{b}|\sin\theta ∣a∣∣b∣sinθ。此过程不仅验证了公式,更暴露了叉乘与点积的隐秘关联:叉乘模长的平方等于向量自身模积平方减去其点积平方,暗示两者共享同一几何本源。
投影与内积:平行分量的代数刻画
若叉乘衡量向量的“垂直张力”,则点积 A ⋅ B \mathbf{A} \cdot \mathbf{B} A⋅B 刻画的是其“平行协同性”:
A ⋅ B = ∣ A ∣ ∣ B ∣ cos θ \mathbf{A} \cdot \mathbf{B} = |\mathbf{A}||\mathbf{B}| \cos \theta A⋅B=∣A∣∣B∣cosθ
该标量值直接引出了投影(Projection)的概念——即一个向量在另一个向量方向上的“影子分量”。向量 A \mathbf{A} A 在 B \mathbf{B} B 方向上的投影向量定义为:
proj B A = ( A ⋅ B ∣ B ∣ 2 ) B \text{proj}_{\mathbf{B}} \mathbf{A} = \left( \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{B}|^2} \right) \mathbf{B} projBA=(∣B∣2A⋅B)B
而投影的标量长度(即投影向量的模)为:
∣ proj B A ∣ = A ⋅ B ∣ B ∣ = ∣ A ∣ cos θ \left| \text{proj}_{\mathbf{B}} \mathbf{A} \right| = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{B}|} = |\mathbf{A}| \cos \theta ∣projBA∣=∣B∣A⋅B=∣A∣cosθ
这一定义直观体现了点积的几何角色:内积是投影长度的缩放因子。当 B \mathbf{B} B 为单位向量时,投影长度简化为 A ⋅ B \mathbf{A} \cdot \mathbf{B} A⋅B,此时点积即为 A \mathbf{A} A 在 B \mathbf{B} B 方向上的直尺度量。
转置左乘:代数符号的几何翻译
在线性代数中,列向量 A , B \mathbf{A}, \mathbf{B} A,B 的内积可通过矩阵运算表达为 A T B \mathbf{A}^T \mathbf{B} ATB。这一形式绝非符号游戏:
- 当 B \mathbf{B} B 是单位向量时, A T B = A ⋅ B = ∣ proj B A ∣ \mathbf{A}^T \mathbf{B} = \mathbf{A} \cdot \mathbf{B} = |\text{proj}_{\mathbf{B}} \mathbf{A}| ATB=A⋅B=∣projBA∣
- 当 B \mathbf{B} B 非单位时, A T B \mathbf{A}^T \mathbf{B} ATB 是计算投影的关键中间量,满足:
proj B A = ( A T B ∣ B ∣ 2 ) B \text{proj}_{\mathbf{B}} \mathbf{A} = \left( \frac{\mathbf{A}^T \mathbf{B}}{|\mathbf{B}|^2} \right) \mathbf{B} projBA=(∣B∣2ATB)B
转置左乘的本质,是将几何投影操作编码为矩阵乘法。这一符号化过程凸显了线性代数作为“几何的语言”的威力——抽象运算与空间直觉在此完美对应。
叉乘与点积的二元统一:几何的阴阳两面
尽管叉乘生成新向量而点积生成标量,两者在深层结构上却构成互补的二元系统:
-
正交与平行的对偶性
- 叉乘模长 ∣ a × b ∣ |\mathbf{a} \times \mathbf{b}| ∣a×b∣ 最大化时,向量正交( sin θ = 1 \sin \theta =1 sinθ=1);
- 点积 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 最大化时,向量平行( cos θ = 1 \cos \theta =1 cosθ=1)。
两者共同覆盖了向量间角度关系的全部可能性。
-
面积与投影的关联
考虑 a \mathbf{a} a 和 b \mathbf{b} b 张成的平行四边形:- 面积由 ∣ a × b ∣ |\mathbf{a} \times \mathbf{b}| ∣a×b∣ 给出;
- 若以 b \mathbf{b} b 为底,其高 h h h 恰为 a \mathbf{a} a 在垂直于 b \mathbf{b} b 方向上的投影长度,即:
h = ∣ a ∣ sin θ = ∣ a × b ∣ ∣ b ∣ h = |\mathbf{a}| \sin \theta = \frac{|\mathbf{a} \times \mathbf{b}|}{|\mathbf{b}|} h=∣a∣sinθ=∣b∣∣a×b∣
此处叉乘模长与投影长度通过几何结构直接连通。
-
广义勾股定理的体现
由恒等式 ∣ a × b ∣ 2 + ( a ⋅ b ) 2 = ∣ a ∣ 2 ∣ b ∣ 2 |\mathbf{a} \times \mathbf{b}|^2 + (\mathbf{a} \cdot \mathbf{b})^2 = |\mathbf{a}|^2 |\mathbf{b}|^2 ∣a×b∣2+(a⋅b)2=∣a∣2∣b∣2 可见:- 叉乘模长平方(面积平方)与点积平方(投影尺度平方)之和等于模积平方。
这恰似一个“向量勾股定理”,暗示垂直分量与平行分量的能量守恒。
- 叉乘模长平方(面积平方)与点积平方(投影尺度平方)之和等于模积平方。
从二维到高维:数学结构的延伸
在二维空间中,叉乘退化为标量(即 a x b y − a y b x a_xb_y - a_yb_x axby−aybx),其绝对值仍表示面积,且与点积共同构成平面旋转群的生成元。至高维空间,叉乘被推广为外积(Wedge Product),而点积保持为内积。此时,外积 a ∧ b \mathbf{a} \wedge \mathbf{b} a∧b 的范数仍正比于 ∣ a ∣ ∣ b ∣ sin θ |\mathbf{a}||\mathbf{b}|\sin\theta ∣a∣∣b∣sinθ,代表高维平行体的体积;内积则继续表征投影。两者在微分几何中共同定义流形的度量与曲率,成为广义相对论与规范场论的数学根基。
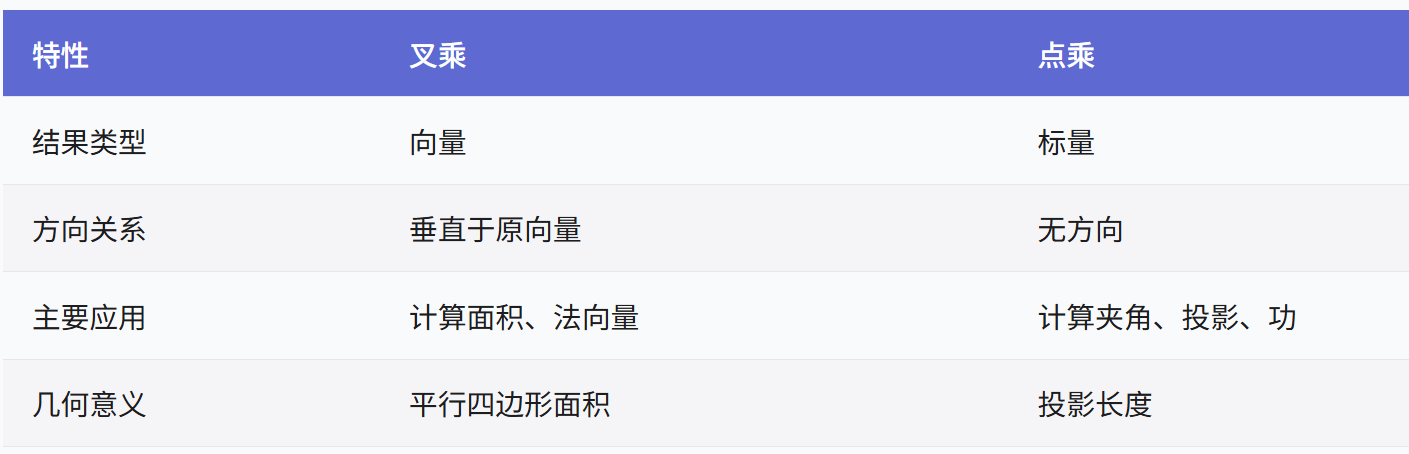
结语:代数为骨,几何为魂
向量叉乘模长与内积投影的讨论,揭示了数学中一个核心范式:抽象符号承载具体直觉,几何现象驱动代数创新。
- ∣ a × b ∣ = ∣ a ∣ ∣ b ∣ sin θ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta ∣a×b∣=∣a∣∣b∣sinθ 不仅是公式,更是对空间张量的度量宣言;
- proj B A = A T B ∣ B ∣ 2 B \text{proj}_{\mathbf{B}} \mathbf{A} = \frac{\mathbf{A}^T \mathbf{B}}{|\mathbf{B}|^2} \mathbf{B} projBA=∣B∣2ATBB 不单是推导,而是线性映射的几何实现;
- 两者通过恒等式 ∣ a × b ∣ 2 + ( a ⋅ b ) 2 = ∣ a ∣ 2 ∣ b ∣ 2 |\mathbf{a} \times \mathbf{b}|^2 + (\mathbf{a} \cdot \mathbf{b})^2 = |\mathbf{a}|^2 |\mathbf{b}|^2 ∣a×b∣2+(a⋅b)2=∣a∣2∣b∣2 达成对称统一,彰显向量运算内在的和谐。
在物理学中,此二元性表现为力矩(叉乘)与功(点积)的并存;在计算机图形学中,它化身法线计算与光照模型的基石;在数据科学中,它成为协方差矩阵与主成分分析的源头。理解这一深层联系,不仅为掌握向量分析提供钥匙,更让我们窥见数学如何以简洁的符号编织空间的经纬——在叉乘与点积的交响中,代数与几何完成了永恒的对话。
