当前位置：首页 > news >正文

算法打卡17天（补）

news 来源：原创 2025/6/9 8:28:50

左叶子之和

（力扣404题）

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

解题思路

题目要求计算二叉树中所有左叶子节点的值之和。采用递归的后序遍历（左-右-中）方法来解决。

递归终止条件：
如果当前节点为空，直接返回0。如果当前节点是叶子节点（没有左右子节点），也返回0，因为叶子节点本身不是左叶子节点。
递归左子树：
递归计算左子树的左叶子节点之和。如果左子树是一个左叶子节点（即左子节点没有左右子节点），则将其值加入到leftValue中。
递归右子树：
递归计算右子树的左叶子节点之和。右子树中可能包含左叶子节点，因此需要继续递归。
计算总和：
将左子树和右子树的左叶子节点值相加，得到当前节点的左叶子节点之和。

通过这种方式，可以逐层递归遍历整棵树，确保所有左叶子节点的值都被正确计算。这种方法利用了后序遍历的思想，确保在处理当前节点时，左右子树的结果已经计算完成。

代码

#include <iostream>
#include <vector>
using namespace std;
// 左叶子之和
struct TreeNode
{int val;TreeNode *left;TreeNode *right;
};
// 后序遍历
class Solution
{public:int sumOfLeftLeaves(TreeNode *root){if (root == NULL){return 0;}// 如果是叶子节点if (root->left == NULL && root->right == NULL){return 0;}// 左int leftValue = sumOfLeftLeaves(root->left);// /遇到左叶子节点if (root->left && !root->left->left && !root->left->right){leftValue = root->left->val;}// 右int rightValue = sumOfLeftLeaves(root->right);// 中int sum = leftValue + rightValue;return sum;}
};

二叉树的右视图

（力扣199题）

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

**输入：**root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

示例 2：

**输入：**root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

**输入：**root = [1,null,3]

输出：[1,3]

示例 4：

**输入：**root = []

输出：[]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

解题思路

使用队列进行层次遍历：通过队列逐层遍历二叉树。每次从队列中取出一层的所有节点，并处理这些节点。
记录每层的最后一个节点：在每一层的遍历中，当索引 i 等于当前层的最后一个节点索引（size - 1）时，将该节点的值加入结果数组。因为右视图只能看到每一层的最右边的节点。
处理子节点：对于每个节点，先将左子节点加入队列，再将右子节点加入队列。这样可以确保在下一层的遍历中，右子节点始终在左子节点之后被处理。
返回结果：遍历完成后，返回结果数组，即为二叉树的右视图。

这种方法利用了层次遍历的特性，通过队列的先进先出特性，逐层处理节点，同时记录每层的最后一个节点，从而实现右视图的获取。

代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// 层级遍历
class Solution
{
public:vector<int> rightSideView(TreeNode *root){queue<TreeNode *> que;// 如果根节点不为空，将根节点加入队列if (root != NULL){que.push(root);}vector<int> result;// 当队列不为空时，继续层次遍历while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){// 取出队列的第一个节点TreeNode *cur = que.front();que.pop();// 如果是当前层的最后一个节点（即右视图能看到的节点），将其值加入结果数组if (i == (size - 1)){result.push_back(cur->val);}// 如果当前节点有左子节点，加入队列if (cur->left){que.push(cur->left);}// 如果当前节点有右子节点，加入队列if (cur->right){que.push(cur->right);}}}return result;}
};
int main()
{// 创建一个测试用的二叉树TreeNode *root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);root->right->right = new TreeNode(6);// 创建 Solution 对象并调用 rightSideView 方法Solution s;vector<int> result = s.rightSideView(root);// 打印结果cout << "Right Side View: ";for(int val: result){cout << val << " ";}cout << endl;delete root->left->left;delete root->left->right;delete root->left;delete root->right->right;delete root->right;delete root;return 0;}

找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

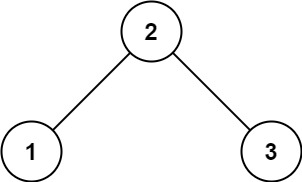
输入: root = [2,1,3]
输出: 1

示例 2:

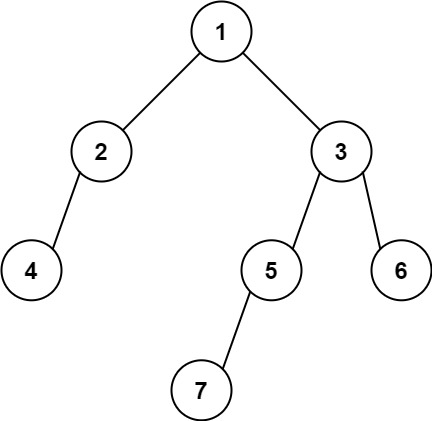
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

1.递归法

解题思路

定义目标：
- 需要找到二叉树中最底层的最左边的值。这意味着我们需要遍历整个二叉树，找到深度最大的叶子节点，并记录其值。
使用深度优先搜索（DFS）：
- 通过递归的方式遍历二叉树的每个节点。
- 在递归过程中，记录当前节点的深度 depth。
记录最大深度和对应值：
- 定义两个全局变量：
  - maxDepth：记录当前遍历到的最大深度，初始值为 INT_MIN。
  - result：记录最底层的最左边的值。
- 在递归过程中，当到达叶子节点时，检查当前深度是否大于 maxDepth。如果是，则更新 maxDepth 和 result。
递归逻辑：
- 对于每个节点，先递归遍历左子节点，再递归遍历右子节点。这样可以确保在相同深度的情况下，左边的节点先被处理。
- 在递归调用时，深度 depth 需要加 1。
- 在递归返回时，深度 depth 需要减 1（回溯）。
终止条件：
- 当到达叶子节点（即没有左右子节点的节点）时，检查当前深度是否大于 maxDepth。如果是，则更新 maxDepth 和 result。
返回结果：
- 遍历完成后，返回 result，即最底层的最左边的值。

代码

class Solution
{
public:// 记录当前遍历到的最大深度int maxDepth = INT_MIN;// 存储最终结果，即最底层的最左边的值int result;// 定义递归遍历函数void traversal(TreeNode *root, int depth){// 当前是叶子节点   递归出口if (root->left == NULL && root->right == NULL){// 检查当前深度是否大于已记录的最大深度if (depth > maxDepth){maxDepth = depth;result = root->val;}return; // 返回上一层递归}// 如果当前节点有左子节点if (root->left){// 深度加1depth++;// 递归遍历左子节点traversal(root->left, depth);// 回溯depth--;}// 如果当前节点有右子节点if (root->right){// 深度加1depth++;// 递归遍历右子节点traversal(root->right, depth);// 回溯depth--;}}int findBottomLeftValue(TreeNode *root){// 从根节点开始traversal(root, 0);return result;}
};

2.迭代法

解题思路

层次遍历：
- 使用队列实现层次遍历。将根节点加入队列，逐层处理节点。
- 每次从队列中取出一层的所有节点，处理它们的子节点。
记录每层的第一个节点：
- 在每一层的遍历中，第一个被弹出的节点即为该层的最左边的节点。
- 使用变量 result 记录每层的第一个节点的值。
更新队列：
- 对于每个节点，先将左子节点加入队列，再将右子节点加入队列。
- 这样可以确保在下一层的遍历中，左子节点先于右子节点被处理。
循环终止：
- 当队列为空时，表示所有层的节点都已处理完毕。
- 最后记录的 result 即为最底层的最左边的值。

通过层次遍历，逐层记录每层的第一个节点，最终返回最底层的最左边的值。这种方法利用了队列的先进先出特性，确保了节点的处理顺序正确。

代码

// 迭代法   层级遍历
class Solution1
{
public:int findBottomLeftValue1(TreeNode *root){queue<TreeNode *> que;if (root != NULL){// 当前节点加入队列que.push(root);}int result = 0;// 队列不为空while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){// 记录队列当前节点并且弹出TreeNode *node = que.front();que.pop();// 记录最后一行第一个元素(左下角的值)if (i == 0){result = node->val;}// 当前节点的左右子树并且加入队列if (node->left){que.push(node->left);}if (node->right){que.push(node->right);}}}return result;}
};

路径总和

(力扣112题)

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

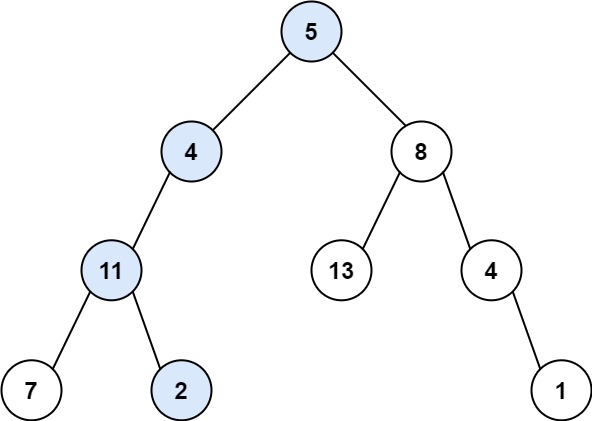
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

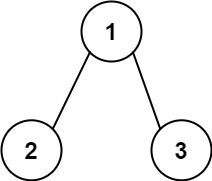
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

解题思路

这道题的解题思路是利用递归遍历二叉树，判断是否存在一条从根节点到叶子节点的路径，使得路径上所有节点的值之和等于目标值 targetSum。

递归终止条件：
- 如果当前节点是叶子节点（即没有左右子节点），并且路径和等于目标值（count == 0），则返回 true，表示找到了满足条件的路径。
- 如果当前节点是叶子节点但路径和不等于目标值（count != 0），则返回 false。
递归处理左右子树：
- 如果当前节点有左子节点，将左子节点的值从路径和中减去（count -= cur->left->val），然后递归检查左子树。
- 如果当前节点有右子节点，将右子节点的值从路径和中减去（count -= cur->right->val），然后递归检查右子树。
- 如果在左子树或右子树中找到了满足条件的路径，则返回 true。
- 如果递归返回后没有找到满足条件的路径，则需要回溯，将减去的值加回来（count += cur->left->val 或 count += cur->right->val）。

代码

#include <iostream>
#include <queue>
using namespace std;
// 路径总和
struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution
{
public:// 定义递归函数，用于判断是否存在路径和等于目标值bool traversal(TreeNode *cur, int count){// 遇到叶子节点，并且计数为0if (cur->left == nullptr && cur->right == nullptr && count == 0){return true;}// 计数不是0if (cur->left == nullptr && cur->right == nullptr && count != 0){return false;}// 如果当前节点有左子节点if (cur->left){count -= cur->left->val;if (traversal(cur->left, count)){return true;}// 回溯，撤销处理结果count += cur->left->val;}// 如果当前节点有左子节点if (cur->right){count -= cur->right->val;if (traversal(cur->right, count)){return true;}// 回溯，撤销处理结果count += cur->right->val;}return false;}bool hasPathSum(TreeNode *root, int targetSum){if (root == nullptr){return false;}return traversal(root, targetSum - root->val);}
};
// 释放节点
void deleteTree(TreeNode *root)
{if (root == nullptr){return;}deleteTree(root->left);deleteTree(root->right);delete root;
}
int main()
{// 创建测试用的二叉树TreeNode *root = new TreeNode(5);root->left = new TreeNode(4);root->right = new TreeNode(8);root->left->left = new TreeNode(11);root->left->left->left = new TreeNode(7);root->left->left->right = new TreeNode(2);root->right->left = new TreeNode(13);root->right->right = new TreeNode(4);root->right->right->right = new TreeNode(1);Solution solution;int targetSum1 = 22;cout << "Test Case 1 - Target Sum: " << targetSum1 << " -> ";if (solution.hasPathSum(root, targetSum1)){cout << "True" << endl;}else{cout << "False" << endl;}deleteTree(root);
}

路径总和ii

(力扣113题)

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

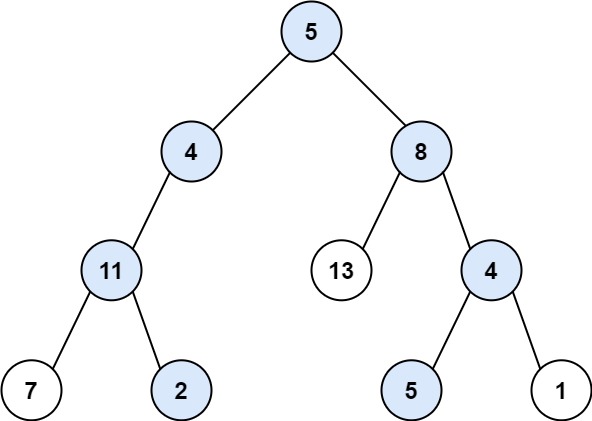
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

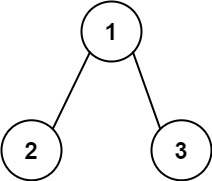
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

这道题的解题思路是利用深度优先搜索（DFS）遍历二叉树，寻找所有从根节点到叶子节点的路径，使得路径上节点值的和等于目标值 targetSum。

解题思路

初始化：
- 使用一个全局变量 result 来存储所有满足条件的路径。
- 使用一个全局变量 path 来存储当前遍历的路径。
递归函数 traversal：
- 终止条件：如果当前节点是叶子节点（没有左右子节点），并且路径和等于目标值（count == 0），则将当前路径 path 添加到结果列表 result 中。
- 叶子节点但路径和不匹配：如果当前节点是叶子节点但路径和不等于目标值（count != 0），直接返回。
- 递归遍历左右子树：
  - 如果当前节点有左子节点，将左子节点的值加入路径，更新路径和（count -= cur->left->val），递归遍历左子树。
  - 如果当前节点有右子节点，将右子节点的值加入路径，更新路径和（count -= cur->right->val），递归遍历右子树。
  - 回溯：在递归返回后，恢复路径和（count += cur->left->val 或 count += cur->right->val），并从路径中移除最后一个节点（path.pop_back()）。

代码

#include <iostream>
#include <queue>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution
{
private:// 用于存储所有满足条件的路径vector<vector<int>> result;// 用于存储当前路径vector<int> path;// 定义递归函数，用于判断是否存在路径和等于目标值void traversal(TreeNode *cur, int count){// 遇到了叶子节点且找到了和为sum的路径if (!cur->left && !cur->right && count == 0){// 将当前路径加入结果列表result.push_back(path);return;}// 遇到叶子节点而没有找到合适的边，直接返回if (!cur->left && !cur->right && count != 0){return;}// 左 （空节点不遍历）if (cur->left){// 将左子节点加入路径path.push_back(cur->left->val);// 更新剩余路径和count -= cur->left->val;// 递归遍历左子树traversal(cur->left, count);// 回溯：恢复剩余路径和 移除路径中的最后一个节点count += cur->left->val;path.pop_back();}// 右子树不为空时，递归遍历右子树if (cur->right){path.push_back(cur->right->val);count -= cur->right->val;traversal(cur->right, count);//    回溯count += cur->right->val;path.pop_back();}}public:vector<vector<int>> pathSum(TreeNode *root, int targetSum){result.clear();path.clear();if (root == NULL)return result;// 把根节点放进路径path.push_back(root->val);traversal(root, targetSum - root->val);return result;}
};
// 释放节点
void deleteTree(TreeNode *root)
{if (root == nullptr){return;}deleteTree(root->left);deleteTree(root->right);delete root;
}
int main()
{// 创建测试用的二叉树TreeNode *root = new TreeNode(5);root->left = new TreeNode(4);root->right = new TreeNode(8);root->left->left = new TreeNode(11);root->left->left->left = new TreeNode(7);root->left->left->right = new TreeNode(2);root->right->left = new TreeNode(13);root->right->right = new TreeNode(4);root->right->right->right = new TreeNode(1);Solution s;int targetSum1 = 22;vector<vector<int>> result = s.pathSum(root, targetSum1);cout << "Test Case 1 - Target Sum: " << targetSum1 << " -> ";//    输出if (!result.empty()){cout << "[";for (int i = 0; i < result.size(); ++i){cout << "[";for (int j = 0; j < result[i].size(); ++j){cout << result[i][j];if (j < result[i].size() - 1){cout << ",";}}if (i < result.size() - 1){cout << ",";}}cout << "]";}else{cout << "[]" << endl;}deleteTree(root);
}