异或和之差-字典树
问题描述
给定一个含有 n 个元素的数组 Ai,你可以选择两个不相交的子段。求出这两个子段内的数的异或和的差值的最大值。
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数 Ai,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
6
1 2 4 9 2 7
样例输出
14
样例说明
两个子段可以分别选 1 和 4,9,2,差值为 15−1=14。
评测用例规模与约定
对于 40 的评测用例,n≤5000;
对于所有评测用例,2≤n≤2×105,0≤Ai≤220。
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 1s | 256M |
| C | 1s | 256M |
| Java | 2s | 256M |
| Python3 | 10s | 256M |
| PyPy3 | 10s | 256M |
| Go | 10s | 256M |
| JavaScript | 10s | 256M |
解析:
看题目,先不考虑相不相交,维护一个i,这个i是之后的分界,考虑前i个元素中某个区间异或和最大或最小,怎么做呢,接下来就考虑字典树(如果字典树不理解先去看什么是字典树问题),将前i个元素求前缀异或和,要求L到R的区间就是[ L-1 ]^[ R ],将这个前缀和写成二进制序列插入到字典树种。异或只与每一位上是0还是1有关,当求出一个前缀和时,要判断字典树中这个区间的最大区间或最小区间,如果求最大区间,就是找与当前这个前缀和异或值最大,去字典树中找相反的记为这个区间最大,找最小时,就是找相同的。如下图所示,
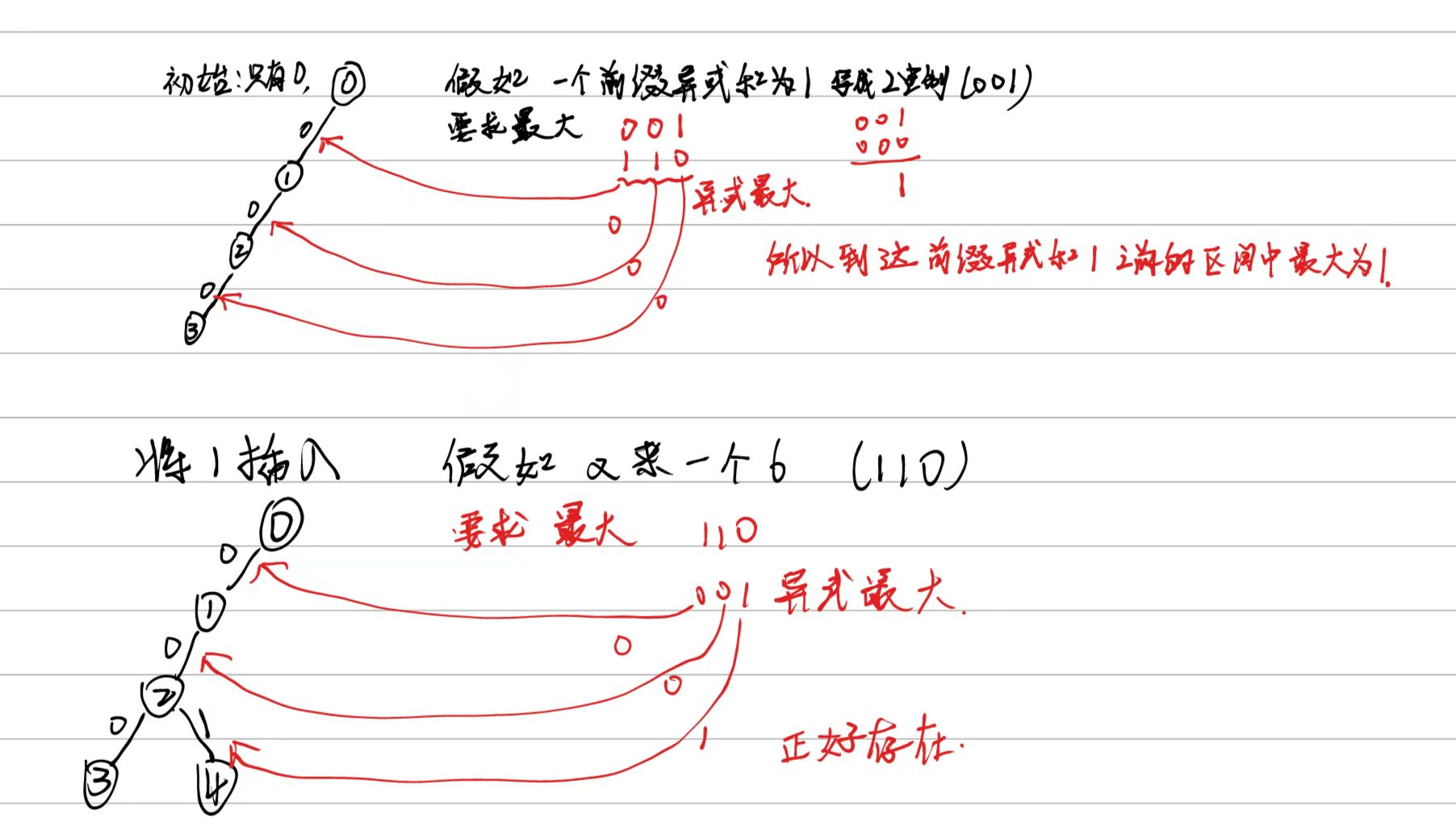
通过i将元素分成两半,对两边分别求最大最小然后作差求最大,将整个数组求前缀异或和,再求后缀异或和,就可以求出两边的最大最小了
代码:
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
typedef long long ll;
const ll MAX = 2e5 + 4;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll a[MAX];//存输入的数组
ll lmax[MAX], lmin[MAX], rmax[MAX], rmin[MAX];//分界线i时左侧的右侧的异或和最大值最小值
ll lsum[MAX],rsum[MAX];//前缀和,后缀和
ll ltree[1<<22][2], rtree[1<<22][2];
int index = 1;//动态节点
void insert(ll x, ll tree[][2])
{int p=0;//节点编号for (int i = 20; i >= 0; i--){int t = (x >> i)&1;if (tree[p][t] == 0){tree[p][t] = index++;}p = tree[p][t];}
}
ll selectMax(ll x,ll tree[][2])//找相反位 只要存在说明异或为1
{int p=0;//节点编号ll res = 0;for (int i = 20; i >= 0; i--){int t = (x >> i) & 1;if (tree[p][!t] != 0){res += (1 << i);p = tree[p][!t];}else {p = tree[p][t];}}return res;
}
ll selectMin(ll x, ll tree[][2])//找相同 只要存在说明异或为0
{int p=0;//节点编号ll res = 0;for (int i = 20; i >= 0; i--){int t = (x >> i) & 1;if (tree[p][t] != 0){p = tree[p][t];}else{res += (1 << i);p = tree[p][!t];}}return res;
}
int main()
{ll n;cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 0; i <= n+1; i++)//初始化{lmax[i] = rmax[i] = 0;lmin[i] = rmin[i] = INF;}//前缀最大最小 i左侧的index = 1;insert(0,ltree);for (int i = 1; i <= n; i++){lsum[i] = lsum[i - 1] ^ a[i];//分为两种情况,包含分界点i和不包含 lmax[i] = max(lmax[i - 1], selectMax(lsum[i], ltree));lmin[i] = min(lmin[i - 1], selectMin(lsum[i], ltree));insert(lsum[i], ltree);}//后缀最大最小 i右侧的index = 1;insert(0, rtree);for (int i = n; i >= 1; i--){rsum[i] = rsum[i + 1] ^ a[i];//分为两种情况,包含分界点i和不包含 rmax[i] = max(rmax[i + 1], selectMax(rsum[i], rtree));rmin[i] = min(rmin[i + 1], selectMin(rsum[i], rtree));insert(rsum[i], rtree);}ll ans = 0;for (int i = 1; i < n; i++)//i表示分界点{//左侧最大-右侧最小//右侧最大-左侧最小//不相交ans = max(ans, max(lmax[i] - rmin[i + 1], rmax[i + 1] - lmin[i]));}cout << ans << endl;return 0;
}