红黑树（原理）c++

红黑树，简称 RBT，也是一颗二叉搜索树。它是在搜索树的基础上，使每个结点增加一个存储位表示结点的颜色，可以是 Red 或者 Black;通过对任意一条从根到叶子的路径上各个结点着色方式的限制，确保没有一条路径会比其他路径长出 2倍，因而是一棵接近平衡的二又搜索树。红黑树相对于 AVL 树来说，牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作，整体来说性能要优于 AVL树。

红黑树的规则:

1. 前提是二叉搜索树;
2. 根结点以及叶子结点是黑色的；（注意，这里的叶子结点不是常规意义上的叶子结点，而是空结点）
3. 红色结点的左右孩子是黑色的；（也就是说，任意一条路径中，不会存在连续的红色结点）
4. 任一结点到叶子结点的路径上，黑色结点的数量相同。

          

• 还有任一结点到叶所有路径黑结点数量相同，11到叶子结点有特别多的路径，上图中有九条路径，其中必须是黑结点数量相同，比如从11走到第一个叶子节点有三个黑色结点，剩下八个也必须一样

总结规则：

• 左根右，左子树中所有的节点的权值小于根节点，根节点的值小于右子树中所有节点的权值，就是二叉搜索树
• 根叶黑，根节点和叶子节点全都是黑色的
• 不红红，同一个路径里面不能出现连续的两个红色节点，这样会违反红色节点的左右孩子必须是黑色的性质
• 黑路同，从当前节点开始，通往所有叶子节点的每条路径里，黑色节点的数量必须得是相同的才行

判断下面的树是否为红黑树

   

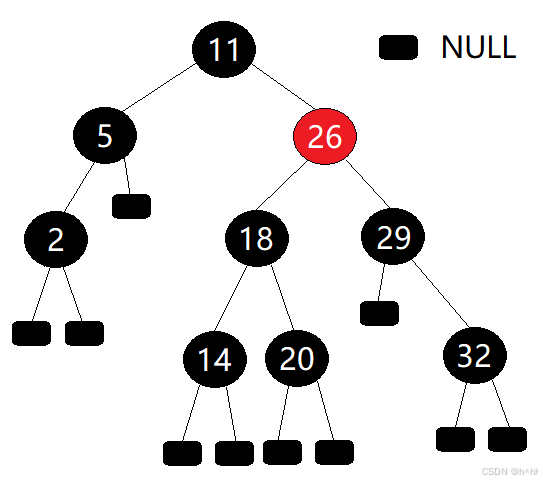
• 符合左根右，根叶黑，不红红规则，不符合黑路同，第一条从根节点到空节点的路径里黑色节点数量是4个，但但三条路径是3个

重要性质

• 最长路径不超过最短路径的两倍

     ​​​​​​

• 正是有这样的特性，导致红黑树的树高h不会超过log以2为底N+1的对数，这样查找删除插入的的时间复杂度，就是log以2为底N的对数

插入

• 按照二叉搜索树的插入方式插入新的结点;
• 默认该点是红色。如果破坏了红黑树的规则，然后就分情况调整成红黑树。

为什么插入节点默认为红色？

比如插入8，如果8是黑色节点，在第2条路径里黑色几点的数量是3，此时从根节点出发到第1、3、4条的路径全都违反了黑路同的规则，这样会导致要调整更多的路径，单单几个节点就要调整3个路径，如果创造10的5次方个节点，要调整数不过来的路径，所以如果插入的是黑色节点，调整起来会很麻烦；而插入红色节点，只可能违反根叶黑或者不红红，相比于插入黑色节点，调整起来比较简单

插入结点后,如果红黑树性质被破坏,分三种情况调整

1.插入结点是根结点

• 直接变黑即可

2.插入结点的叔叔是红色

• 叔父爷变色，爷爷变成插入节点，继续重复调整（此图根节点的右孩子是叔叔）

 3.插入结点的叔叔是黑色

• （LL, RR, LR, RL）旋转，然后变色（此图叔叔节点是NULL，红黑树里的NULL也是黑色节点）

通过构建红黑树，加深一下红黑树的插入操作