【优选算法】前缀和

一：一维前缀和

#include <iostream>
#include <vector>
using namespace std;int main() {int n = 0, q = 0;cin >> n >> q;vector<long long> arr(n+1);for(size_t i = 1; i <= n; i++) cin >> arr[i];// 构建前缀和数组vector<long long> dp(n+1);for(size_t i = 1; i <= n; i++) dp[i] = arr[i]+dp[i-1];int r = 0, l = 0;while(q--){cin >> r >> l;cout << dp[l]-dp[r-1] << endl;}return 0;
}

二：二维前缀和

#include <iostream>
#include <vector>
using namespace std;int main() {// 1.读入数据int n, m, q;cin >> n >> m >> q;vector<vector<int>> arr(n+1, vector<int>(m+1));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> arr[i][j];}}// 2.构建前缀和数组vector<vector<long long>> dp(n+1, vector<long long>(m+1));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1]-dp[i-1][j-1] + arr[i][j];}}// 3.使用前缀和数组int x1 = 0, y1 = 0, x2 = 0, y2 = 0;while(q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1] << endl;}return 0;
}

三：寻找数组的中心下标

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);// 1.预处理前缀和数组和后缀和数组for(int i = 1; i < n; i++)f[i] = f[i-1] + nums[i-1];for(int i = n-2; i >= 0; i--)g[i] = g[i+1] + nums[i+1];// 使用for(int i = 0; i < n; i++)if(f[i] == g[i])return i;return -1;}
};

四：除自身以外数组的乘积

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);// 1.预处理前缀和数组和后缀和数组f[0] = 1, g[n-1] = 1;for(int i = 1; i < n; i++)f[i] = f[i-1]*nums[i-1];for(int i = n-2; i >=0; i--)g[i] = g[i+1]*nums[i+1];// 2.使用vector<int> ret(n);for(int i = 0; i < n; i++)ret[i] = f[i]*g[i];return ret;}
};

五：和为K的子数组

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0] = 1;int sum = 0, ret = 0;for(auto& e : nums){sum += e;if(hash.count(sum-k)) ret += hash[sum-k];hash[sum]++;}return ret;}
};

六：和可被K整除的子数组

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0%k] = 1;int sum = 0, ret = 0;for(auto e : nums){sum += e;int r = (sum % k + k)%k;if(hash.count(r)) ret += hash[r];hash[r]++;}return ret;}
};

七：连续数组

class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int, int> hash;hash[0] = -1;int sum = 0, ret = 0;for(int i = 0; i < nums.size(); i++){sum += nums[i] == 0?-1:1;if(hash.count(sum)) ret = max(ret, i-hash[sum]);else hash[sum] = i;}return ret;}
};

八：矩阵区域和

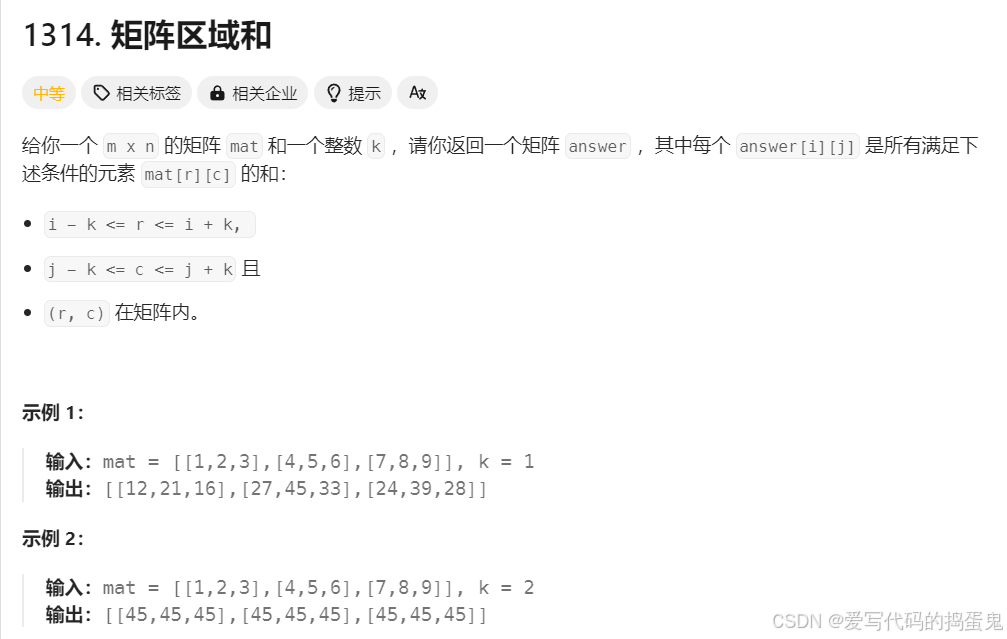
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();// 1.预处理一个前缀和矩阵vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];// 2.使用vector<vector<int>> ret(m, vector<int>(n));for(int i = 0; i < m; i++)for(int j = 0; j < n; j++){int x1 = max(0, i-k)+1, y1 = max(0, j-k)+1;int x2 = min(m-1, i+k)+1, y2 = min(n-1, j+k)+1;ret[i][j] = dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];}return ret;}
};