当前位置：首页 > news >正文

【leetcode】递归，回溯思想 + 巧妙解法-解决“N皇后”，以及“解数独”题目

news 来源：原创 2025/6/8 7:05:44

📚️前言

🌟 本期内容亮点：我们将深入解析力扣（LeetCode）上的几道经典算法题，涵盖不同难度和题型，帮助大家掌握解题思路和代码实现技巧。无论是准备面试还是提升算法能力，这些题解都能为你提供实用参考~

🌈 更多精彩内容：

欢迎访问小编的主页：GGBondlctrl-CSDN博客（点击跳转）
主页涵盖数据结构、算法、编程竞赛、面试经验等丰富内容，持续更新中！

🔥 你的支持很重要：
如果觉得内容对你有帮助，别忘了点赞👍 + 收藏⭐！你的鼓励是小编持续创作优质内容的动力~

🎆 直接进入正题：下面我们将从题目描述、解题思路、代码实现（附详细注释）和复杂度分析等方面，逐一拆解这几道力扣题目，助你高效攻克算法难关！

📚️前言

📚️1.N皇后

1.1题目描述

1.2题目解析

1.3题目代码

📚️2.有效的数独

2.1题目描述

2.2题目解析

2.3题目代码

📚️3.解数独

3.1题目描述

3.2题目解析

3.3题目代码

📚️4.总结

📚️1.N皇后

1.1题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

如下图所示：

这里就是正确的排列方式，为啥呢，看下所示：

可以看到连线的几个方向都是没有问题的；

1.2题目解析

对于N皇后，大家都知道使用递归回溯进行解决，让小编来说说具体的实现方法；

对于这种题目来说，首先我们就要画出这个决策树，这是非常重要的一步，如下所示：

小编这里就不再过多进行延伸了，那么小编就从这里开始讲解吧，很明显这里就是回溯，然后进行剪枝操作，所以重点就是如何进行剪枝呢???

如何剪枝操作：

皇后位置合法性判定逻辑
要确定棋盘上某个位置是否可以放置皇后，需要检查该位置的四个方向（行、列）以及两条对角线。可以通过循环遍历这些方向，判断是否存在其他皇后冲突。

数学优化与哈希表应用
利用数学规律（如行列坐标关系）可以高效判断对角线上是否存在皇后。同时，结合哈希表记录已占用的行、列及对角线，可以进一步优化查询速度，将时间复杂度降低至 O(1)。

第一种思路小编就不讲解了，小编着重讲解一下数学优化和哈希表的应用；

1.对于每一行，我们可以作为参数，来告诉我们的dfs，我们要对于那一行进行判断，那么这里的行就已经是判断，每一行只能是一个皇后1，就如小编上述所画；

2.对于每一列来说，我们可以使用boolean类型数组，来表示这一列是否存在皇后，若存在，那么对应的列来说就是true,那么就可以进行剪枝操作；

3.对于右对角线来说，如下图所示：

可以发现，一个位置的右对角线，可以使用上述图中函数进行表示，那么就有:

boolean[ y - x] = boolean[ b]

此时我们发现存在 b < 0 的情况，因此需要加上一个 row 值。若对角线上存在有效值，则返回 true；若返回 false，则表明对角线上不存在有效值。

4.对于左对角来说，如下图所示：

若某位置已有皇后，则满足 boolean[y + x] = boolean[b] = true 在放置新皇后时，可通过上述条件判断左对角线是否存在冲突

5.对于函数头的设计，那么就是我们需要给定dfs函数一个行数，然后对于每一列进行递归操作，实现我们的目的；

6.递归出口来说，就是当我们的row == 我们的N，就是已经越界了，说明之前的任务已经完成了，那么就以按照题意来进行输出的操作；

好啦，以上就是小编的思路见解，希望能够帮助你~~~~

1.3题目代码

如下所示：

class Solution {boolean[] col;boolean[] digt1;boolean[] digt2;int n;List<List<String>> ret;char[][] path;public List<List<String>> solveNQueens(int _n) {n = _n;path = new char[n][n];col = new boolean[n];digt1 = new boolean[2 * n];digt2 = new boolean[2 * n];ret = new ArrayList<>();//遍历我们的二维数组进行填充for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){path[i][j] = '.';}}dfs(0);return ret;}public void dfs(int row){if(row == n){List<String> tmp = new ArrayList<>();for(int i = 0; i < n; i++){        tmp.add(new String(path[i]));        }ret.add(tmp);return;}//函数体for(int i = 0; i < n; i++){if(col[i] == false && digt1[row - i + n] == false && digt2[row + i] == false){path[row][i] = 'Q';col[i] = digt1[row - i + n] = digt2[row + i] = true;dfs(row + 1);path[row][i] = '.';col[i] = digt1[row - i + n] = digt2[row + i] = false;}}}
}

解析：

对于要使用的参照布尔数组来说，小编设置为全局的；

当然这里还是要注意在满足递归出口条件时，我们的函数返回，以及如何添加到全局返回结果ret中，需要仔细操作；

在函数体中，我们按照上述分析进行剪枝操作；

然后进行修改，并将对应的参照数组进行修改，然后进行递归，返回后我们要恢复我们的现场，包括棋盘，以及我们的参照数组；

📚️2.有效的数独

2.1题目描述

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

2.2题目解析

第一种思路：

我们拿到一个数之后，我们可以遍历这个数的列，以及行；依次进行遍历；然后对于这个数的区域在进行遍历判断，但是这里的时间复杂符比较高

第二种思路：

利用哈希思想，这里我们对于每一行，以及每一列设置参照函数：

boolean[ row ][ num ]

boolean[ col ][ num ]

那么上述第一个row ,col代表的含义就是对应的哪一行，那一；然后后面的数字就是我们的目标判断值；当第一行出现了5：

boolean[ 1 ][ 5 ] == true;

当第一行又出现了 5，那么可以判断此时boolean [ 1 ][ 5 ]进行判断此时的值是否是false

我们的列也是如此

对于我们的三个小方格，那么也是同样的方式，但是如何确定一个位置，是属于那个小方格呢

如下图所示：

那么设计的布尔数组就是：

boolean[ x / 3 ] [ y / 3 ] [ num ]

表示属于哪个方格，然后对应的数值是多少

2.3题目代码

代码如下所示：

class Solution {public boolean isValidSudoku(char[][] board) {boolean[][] row = new boolean[9][10];boolean[][] col = new boolean[9][10];boolean[][][] grid = new boolean[3][3][10];for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if (board[i][j] != '.') {int num = board[i][j] - '0';if (row[i][num] == true || col[j][num] == true || grid[i / 3][j / 3][num] == true) {return false;}row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;}}}return true;}
}

注意：

当我们遇到一个非“.”的数字时，需要根据预先设置的布尔数组进行判断。如果该数字已存在于同一行、同一列或同一个3×3方格中，则返回false；否则，我们将更新布尔数组的记录。

📚️3.解数独

3.1题目描述

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

需要填充的数组：

目标已经填写的数组：

3.2题目解析

本题就是使用递归的操作，就是对于每个空进行遍历，然后进行递归操作，但是注意了会存在以下的情况：

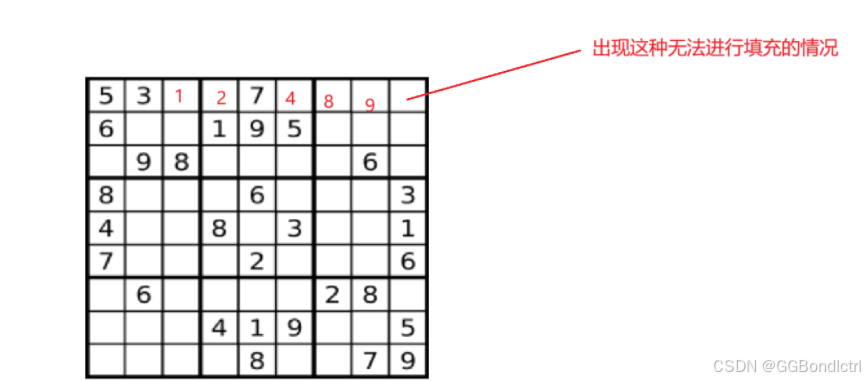
那么我们在设计我们的函数头的时候，对于什么时候是我们的递归出口，是很难判断的，那么此时我们就要进行递归的操作，但是正确的填法，我们不需要进行递归的操作，那么我们此时可以规定我们的函数头是存在一个返回值的；

那么对的就不是像普遍的深度优先搜索，那么每个节点都要进行递归，那么上述题目只有到一个不正确的情况才会进行回溯；

注意：这里的递归出口是很难进行操作的，所以这里使用剪枝，将不对的棋盘操作全部剪掉，留下的就是一个正确的棋盘；（那么这里就不需要所谓的递归出口了）

当然进行剪枝的时候，还是利用上述“有效数独题目”进行判断剪枝

3.3题目代码

代码如下所示：

class Solution {boolean[][] row;boolean[][] col;boolean[][][] grid;public void solveSudoku(char[][] board) {row = new boolean[9][10];col = new boolean[9][10];grid = new boolean[3][3][10];for(int i = 0; i < 9; i++){for(int j = 0; j < 9; j++){if(board[i][j] != '.'){int num = board[i][j] - '0';row[i][num] = col[j][num] = grid[i/3][j/3][num] = true;}}}dfs(board);}public boolean dfs(char[][] board) {for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if (board[i][j] == '.') {for (int pos = 1; pos <= 9; pos++) {if(row[i][pos] == false && col[j][pos] == false && grid[i/3][j/3][pos] == false){board[i][j] = (char)(pos + '0');row[i][pos] = col[j][pos] = grid[i/3][j/3][pos] = true;if(dfs(board)){//这里为真表示可以填数字，那么就不用回溯，进行下一个空格的填写return true;}//说明这里有不能填写的空格，那么就要恢复现场board[i][j] = '.';row[i][pos] = col[j][pos] = grid[i/3][j/3][pos] = false;}}return false;}}}return true;}
}

解析：

首先我们要对于原始数组进行布尔数组的设置，方便后序的剪枝操作

然后对于每个节点进行递归操作，在进行剪枝

若我们拿到的递归函数的值为true,说明没有问题，不用进行回溯，继续填充

相反若在if条件判断之外，那么就说明这次没有办法填充，那么返回false

最后循环完成后，说明所有的空填完了，那么直接返回true即可

📚️4.总结

本文系统介绍了回溯算法在棋盘类问题中的应用：

N皇后问题：通过递归逐行放置皇后，利用布尔数组记录列、左右对角线的占用情况（col[i]、digt1[row-i+n]、digt2[row+i]），实现冲突检测与剪枝，高效输出所有合法解。
数独问题：
- 有效数独验证：通过行列宫三组布尔数组（row[i][num]、col[j][num]、grid[i/3][j/3][num]）快速检测数字重复。
- 解数独：基于回溯框架，对空格尝试数字1-9，结合布尔数组剪枝，通过递归返回值控制回溯路径，找到唯一解即终止。