NLP学习路线图(二十六):自注意力机制
一、为何需要你?序列建模的困境
在你出现之前,循环神经网络(RNN)及其变种LSTM、GRU是处理序列数据(如文本、语音、时间序列)的主流工具。它们按顺序逐个处理输入元素,将历史信息压缩在一个隐藏状态向量中传递。
-
瓶颈显现:
-
长程依赖遗忘: 随着序列增长,早期信息在传递过程中极易被稀释或丢失。想象理解一段长文时,开篇的关键人物在结尾被提及,RNN可能已“忘记”其重要性。
-
并行化困难: 顺序处理特性严重阻碍了利用现代GPU/TPU强大并行计算能力,训练效率低下。
-
信息瓶颈: 无论序列多长,RNN都试图将所有历史信息塞进一个固定长度的隐藏向量中,导致信息损失。
-
这些限制呼唤着一种能直接建模序列元素间任意距离依赖关系,且高度并行的机制。你——自注意力机制,应运而生。
二、深入你的核心:工作原理与数学解析
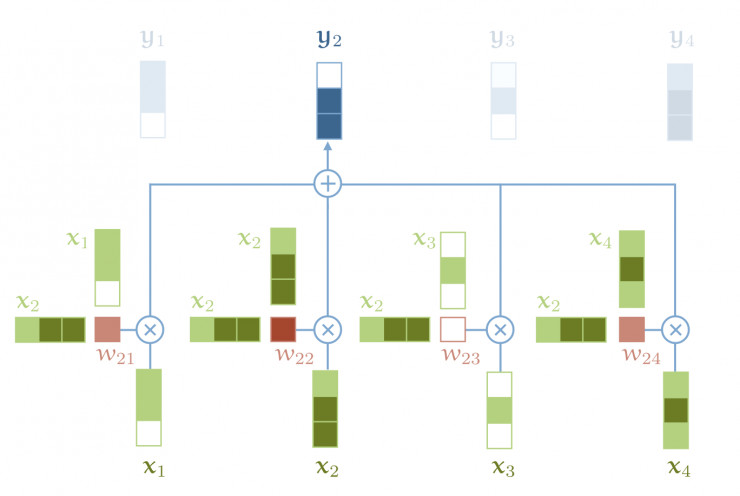
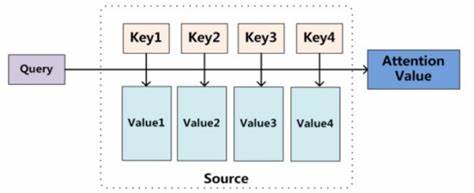
你的核心思想直击要害:序列中的每个元素,都应该能直接关注到序列中所有其他元素(包括自己),并根据它们的重要性(相关性)动态地聚合信息。 让我们拆解这一过程:
-
输入表示:
-
假设我们有一个输入序列,包含
n个元素(如单词):X = [x₁, x₂, ..., xₙ],其中每个x_i是一个d_model维的向量(通常是词嵌入)。 -
将
X堆叠成矩阵:X ∈ ℝ^(n × d_model)。
-
-
线性投影:生成Q, K, V:
-
为每个输入元素
x_i创建三个不同的向量表示:-
查询向量 (Query, q_i): 表示当前元素“正在寻找什么”。它像一个问题:“哪些信息与我相关?”
-
键向量 (Key, k_i): 表示当前元素“能提供什么”。它像一个标识符,用于匹配查询。
-
值向量 (Value, v_i): 表示当前元素“实际包含的信息内容”。它是在匹配成功后将被提取的信息。
-
-
通过可学习的权重矩阵
W^Q,W^K,W^V(每个维度为d_model × d_k或d_model × d_v,通常d_k = d_v)进行线性投影:Q = X * W^Q # Q ∈ ℝ^(n × d_k) K = X * W^K # K ∈ ℝ^(n × d_k) V = X * W^V # V ∈ ℝ^(n × d_v)
-
-
计算注意力分数:
-
目标:计算序列中 每个元素(作为查询) 对所有元素(包括自己,作为键)的“关注程度”(相关性分数)。
-
方法:计算查询向量
q_i与 所有 键向量k_j(j=1 to n) 的点积。点积衡量向量间的相似度(夹角越小,点积越大)。Score(q_i, k_j) = q_i · k_j^T -
将所有查询对所有键的分数组合起来,形成一个
n × n的注意力分数矩阵S:S = Q * K^T # S ∈ ℝ^(n × n) -
示例: 考虑句子 “The animal didn’t cross the street because it was too tired”。计算
it(作为Query) 的注意力分数时,理想情况下,it与animal和street的点积应较高(语义相关),而与didn’t、cross等的点积应较低。
-
-
缩放 (Scaling):
-
点积的值可能随着向量维度
d_k的增大而变得非常大(方差增大),导致Softmax后的梯度变得极小(梯度消失问题)。 -
解决方案:将分数除以
√d_k进行缩放,稳定梯度。S_scaled = S / √d_k
-
-
应用Softmax:获取注意力权重:
-
对
S_scaled矩阵的 每一行 应用Softmax函数。 -
作用: 将每个查询对应的那一行分数(与所有键的相关性)转换为概率分布(和为1)。
A = softmax(S_scaled, dim=-1) # A ∈ ℝ^(n × n) -
矩阵
A称为 注意力权重矩阵。元素A_ij表示当生成第i个位置的输出时,应该给予第j个输入位置多少关注度(权重)。 -
示例 (续): 对于
it对应的行,A_it, animal和A_it, street的权重会接近0.5(假设两者都相关),而其他位置的权重接近0。
-
-
加权求和:生成输出表示:
-
使用注意力权重矩阵
A对值向量矩阵V进行加权求和。 -
对于输出序列中的第
i个位置,其输出向量z_i是:z_i = Σ_j (A_ij * v_j) -
矩阵形式:
Z = A * V # Z ∈ ℝ^(n × d_v) -
输出矩阵
Z的每一行z_i是输入序列所有值向量的加权组合,权重由i位置对应的查询与所有键的匹配程度决定。 -
示例 (续):
z_it将是v_animal和v_street的加权组合(权重各约0.5),融合了这两个关键实体的信息,帮助模型正确理解it指代animal。
-
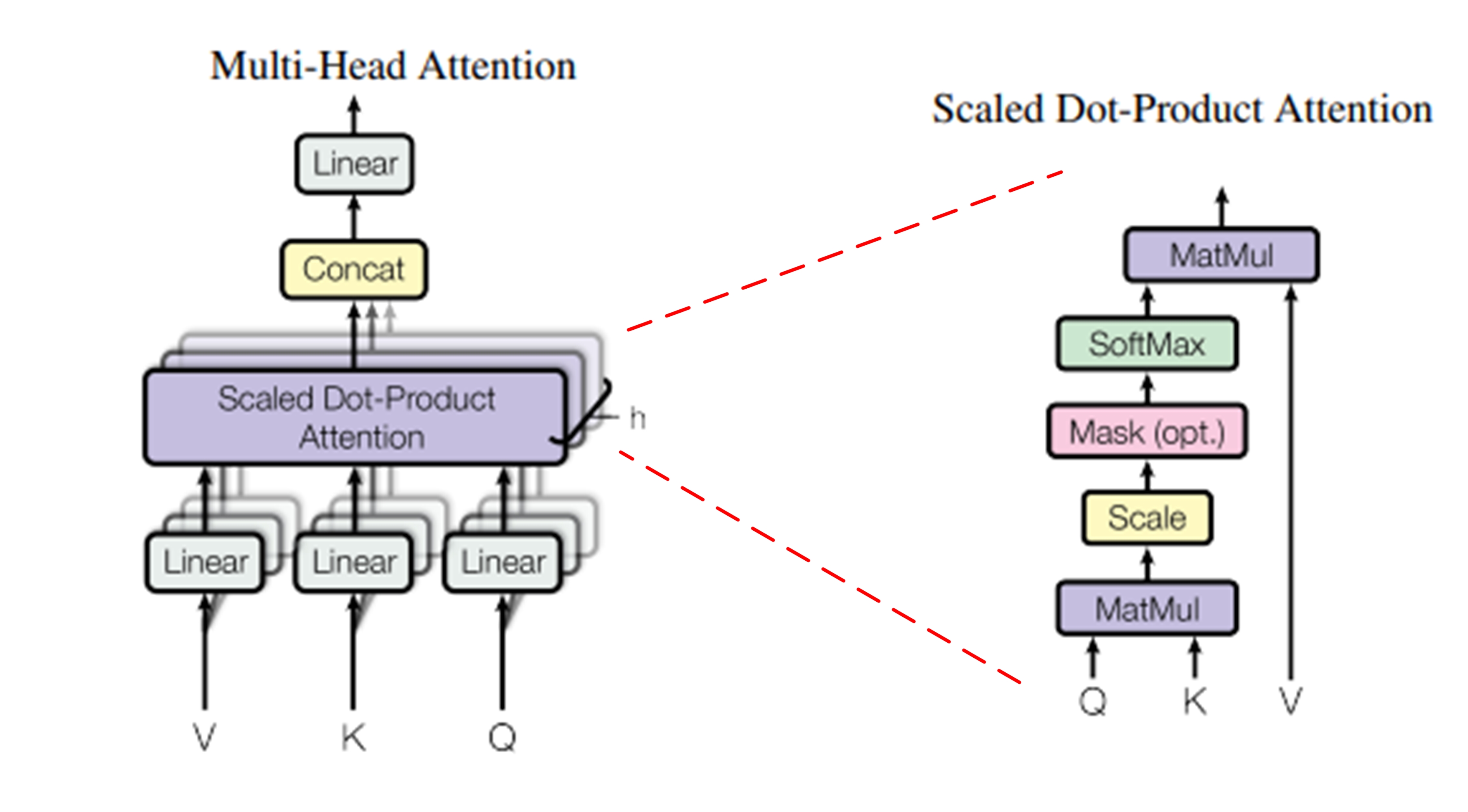
三、你的超能力:多头注意力 (Multi-Head Attention)
单一的自注意力机制捕捉到的关系模式可能有限。你进化出了更强大的形态——多头注意力:
-
并行化投影:
-
不再只使用一组
W^Q, W^K, W^V,而是使用h组不同的投影矩阵{W^Q_l, W^K_l, W^V_l} for l=1 to h。 -
将输入
X分别投影到h组不同的Q_l, K_l, V_l子空间。每组投影将输入向量映射到较低的维度(d_k' = d_k / h,d_v' = d_v / h)。
-
-
并行计算:
-
在每组投影后的
(Q_l, K_l, V_l)上 独立并行地 执行前面描述的缩放点积注意力计算,得到h个输出矩阵Z_l ∈ ℝ^(n × d_v')。
-
-
拼接与线性变换:
-
将所有
h个头的输出Z_l拼接 (Concatenate) 起来:Concat(Z_1, Z_2, ..., Z_h) ∈ ℝ^(n × (h * d_v'))。 -
通过一个可学习的线性投影矩阵
W^O ∈ ℝ^(h*d_v' × d_model)将拼接后的结果映射回原始的d_model维度:MultiHead(Q, K, V) = Concat(head_1, ..., head_h) * W^O where head_l = Attention(Q * W^Q_l, K * W^K_l, V * W^V_l)
-
-
为何强大?
-
捕捉不同关系模式: 不同的投影子空间允许每个“头”关注输入序列的不同方面或关系类型(例如,一个头关注句法依赖,一个头关注语义角色,一个头关注局部共现)。
-
增强表示能力: 相当于将模型的表征空间分解为多个子空间,并在这些子空间中学习不同的交互模式,最后再融合,极大地增强了模型的表达能力。
-
并行效率: 多个头的计算是完全独立的,可以高效并行。
-

四、位置信息的融入:位置编码 (Positional Encoding)
你有一个关键的特性:置换不变性 (Permutation Invariance)。输入序列的顺序改变(单词位置互换),只要内容相同,计算出的 Q, K, V 矩阵以及注意力权重矩阵 A 在行/列置换的意义下是相同的。这意味着你本身 无法感知元素的顺序信息!这对于理解语言(依赖词序)是灾难性的。
解决方案:位置编码 (Positional Encoding, PE)
-
思想: 为输入序列中每个元素的嵌入向量
x_i显式地注入其位置i的信息。 -
方法: 生成一个与输入嵌入
x_i维度相同 (d_model) 的位置向量p_i,然后将其加到x_i上:x'_i = x_i + p_i -
经典实现 (正弦/余弦波):
-
使用不同频率的正弦和余弦函数:
PE(pos, 2i) = sin(pos / 10000^(2i / d_model)) PE(pos, 2i+1) = cos(pos / 10000^(2i / d_model))-
pos:单词在序列中的位置(0, 1, 2, ...)。 -
i:维度索引(0 ≤ i < d_model/2)。
-
-
优点:
-
能唯一编码任意位置。
-
能相对轻松地学习到位置间的相对关系(
PE_pos + PE_offset可以表示为PE_pos的线性函数)。 -
值域有界([-1, 1]),适合模型处理。
-
-
-
可学习的位置嵌入 (Learned Positional Embeddings): 将位置
pos也视为一个需要学习的嵌入向量(类似词嵌入)。BERT等模型常用此方法。 -
作用: 通过
x'_i = x_i + p_i,你处理的实际输入就包含了“我是谁”(词义)和“我在哪”(位置)的信息,从而能够建模序列的顺序结构。
五、你在Transformer架构中的核心地位
你(通常以多头形式)是Transformer编码器和解码器层中无可替代的核心组件:
-
编码器 (Encoder):
-
输入:源序列(例如待翻译的句子)。
-
结构:由
N个相同的层堆叠而成。 -
每层核心子层:
-
多头自注意力层 (Multi-Head Self-Attention): 让序列中的每个单词关注源序列中所有单词(包括自身),学习源句内部的依赖关系。
-
前馈神经网络层 (Position-wise Feed-Forward Network): 对每个位置的表示进行独立变换(通常包含非线性激活)。
-
-
每个子层周围有:残差连接 (Residual Connection) + 层归一化 (Layer Normalization)。这是稳定深层训练的关键 (
SubLayerOutput = LayerNorm(x + SubLayer(x)))。 -
作用: 为源序列生成富含上下文信息的表示。
-
-
解码器 (Decoder):
-
输入:目标序列(例如正在生成的翻译句子),通常右移一位(Teacher Forcing训练)。
-
结构:也由
N个相同的层堆叠而成。 -
每层核心子层:
-
带掩码的多头自注意力层 (Masked Multi-Head Self-Attention): 让目标序列中的每个单词只能关注它自身及之前的位置(防止信息泄露,保证自回归生成)。这是通过在计算注意力分数时,将“未来”位置的分数设置为负无穷大(经Softmax后变为0)来实现的。
-
多头编码器-解码器注意力层 (Multi-Head Encoder-Decoder Attention): 这一层的
Q来自解码器上一层的输出,而K和V来自编码器最终的输出。这允许解码器中的每个位置关注源序列中的所有位置,获取与当前生成目标词最相关的源信息。 -
前馈神经网络层 (Position-wise Feed-Forward Network)。
-
-
同样,每个子层周围有残差连接和层归一化。
-
作用: 基于编码器提供的源信息以及已生成的目标序列,自回归地预测下一个目标词。
-
六、你带来的革命与深远影响
自注意力机制,你赋予了Transformer模型一系列颠覆性的优势:
-
无与伦比的长程依赖建模: 序列中任意两个元素间的依赖关系,无论距离多远,都只需一步计算即可建立联系。彻底解决了RNN的长程依赖难题。
-
极致并行计算: 矩阵乘法 (
Q*K^T,A*V) 是现代硬件加速(GPU/TPU)的绝佳搭档。训练速度比RNN快几个数量级。 -
强大的表征学习能力: 通过动态加权聚合全局信息,为序列中的每个元素生成高度上下文化的表示。多头机制进一步增强了捕捉复杂模式的能力。
-
架构简洁优雅: 核心计算基于线性变换和矩阵乘法,结构清晰,易于理解和扩展。
七、你的辉煌舞台:现代大模型的基石
你的思想已成为当今几乎所有最先进NLP模型的基石:
-
BERT (Bidirectional Encoder Representations from Transformers):
-
本质:仅使用Transformer编码器堆叠。
-
预训练任务:
-
Masked Language Model (MLM): 随机掩盖输入句子中的部分单词,让模型基于上下文预测被掩盖的词。这迫使模型学习强大的双向上下文表示。
-
Next Sentence Prediction (NSP): 判断两个句子是否是连续的上下文关系。
-
-
影响: 开创了“预训练+微调”范式。其强大的上下文表示能力在众多下游任务(文本分类、问答、NER等)上取得突破性进展。
-
-
GPT (Generative Pre-trained Transformer) 系列:
-
本质:仅使用Transformer解码器堆叠(注意:GPT的解码器块去除了编码器-解码器注意力层,只保留带掩码的自注意力和前馈层)。
-
预训练任务:自回归语言建模。 根据上文预测下一个词。强大的生成能力是其核心。
-
演进:
-
GPT-1:证明仅解码器架构的有效性。
-
GPT-2:更大规模,展示零样本/少样本学习潜力。
-
GPT-3:庞大规模(1750亿参数),强大的上下文学习 (In-Context Learning) 和提示 (Prompting) 能力震惊世界。
-
GPT-4 / ChatGPT:多模态、对话能力、指令遵循能力达到新高度。
-
-
影响: 引领了大语言模型 (LLM) 和生成式AI的浪潮。
-
-
其他闪耀明星:
-
T5 (Text-to-Text Transfer Transformer): 将所有NLP任务统一转换为“文本到文本”的格式(如输入
"translate English to German: ..."),使用标准的编码器-解码器Transformer架构处理。 -
RoBERTa, ALBERT, DistilBERT 等: 对BERT的优化(如动态掩码、移除NSP、参数共享、模型蒸馏),追求更高效或更强大的表示。
-
Transformer-XL, Longformer, BigBird: 致力于克服Transformer在超长序列上计算复杂度高 (
O(n²)) 和内存消耗大的问题,引入分块、稀疏注意力(局部+全局)、随机注意力等机制。 -
ViT (Vision Transformer): 开创性地将Transformer应用于计算机视觉。将图像分割成块 (Patches),视为序列输入Transformer编码器处理,在图像分类等任务上媲美甚至超越CNN。证明了你的通用性。
-
多模态模型 (CLIP, DALL·E, Flamingo): 利用Transformer架构处理文本、图像、音频等多种模态信息,学习它们之间的对齐和联合表示。
-
