当前位置：首页 > news >正文

实数域上的二分

news 来源：原创 2025/6/6 8:49:14

实数域上的二分需注意精度，若要保留k位小数，则精度eps = 10的-(k + 2)次方。若不确定精度则在二分时循环给定次。

实数域上的二分基础

OpenJudge - 02:二分法求函数的零点

画出函数图像，f(x)具有单调性，可用二分。

代码如下：

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;double f_check(double x) {return pow(x, 5) - 15 * pow(x, 4) + 85 * pow(x, 3) - 225 * pow(x, 2) + 274 * x - 121;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);double L = 1.5, R = 2.4, mid = 0.0, eps = 1e-8;while (L + eps < R) {mid = (L + R) / 2.0;if (f_check(mid) < 0)  R = mid;else  L = mid;}cout << fixed << setprecision(6) << L;return 0;
}

当f_check(mid) < 0时，答案在区间左半段，R = mid ≠ mid - 1，因为精度问题，当R = mid - 1时错过答案。当f_check(mid) >= 0时，L= mid。

实数域二分转化为整数域二分

P1577 切绳子 - 洛谷

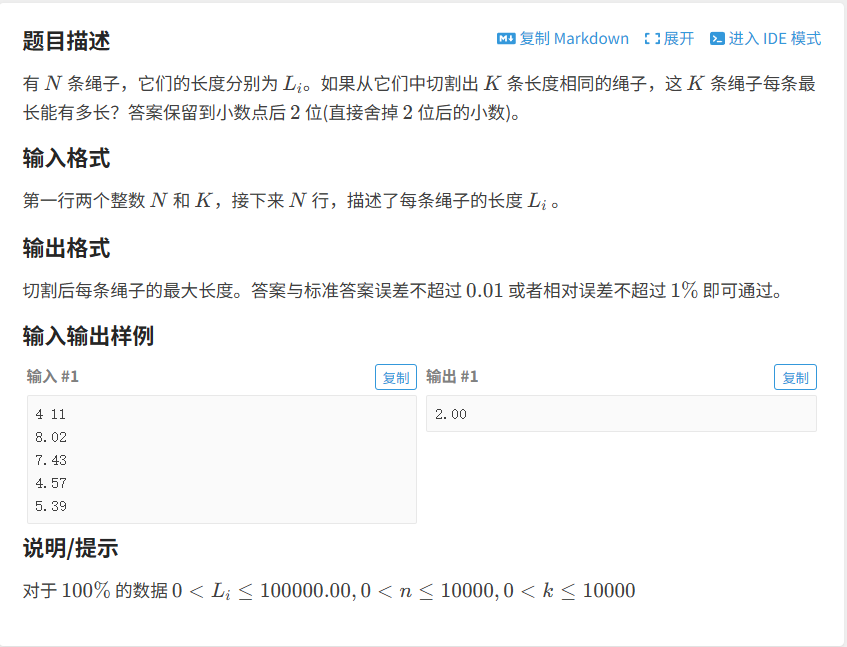
答案保留两位小数，可把输入的Li*100转换成整数，最后的答案/100即可。设最大长度为S，则>S不是解，<S不是最优解，问题具有单调性，用二分答案。

这道题的关键是将小数转换成整数处理。

代码如下：

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;typedef long long LL;const LL Maxn = 1e4 + 5;LL vct[Maxn];LL f_check(LL x, LL n, LL k) {LL num = 0;for (LL i = 1; i <= n; ++i) {num += vct[i] / x;}return num >= k;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);LL n, k, mVal = 0;double inNum = 0;cin >> n >> k;for (LL i = 1; i <= n; ++i) {cin >> inNum;vct[i] = static_cast<LL> (inNum * 100);mVal = max(mVal, vct[i]);}LL L = 1, R = mVal, mid = 0;while (L < R) {mid = L + ((R - L) >> 1) + 1;if (f_check(mid, n, k) != false)  L = mid;else  R = mid - 1;}cout << fixed << setprecision(2) << static_cast<double> (L * 1.0 / 100);return 0;
}

查找多个解

P1024 [NOIP 2001 提高组] 一元三次方程求解 - 洛谷

x1<x2，f(x1)×f(x2)<0，则在 (x1,x2) 之间一定有一个根，此时具有单调性，可用二分。

若一个范围内只有一个根就好了，实根的范围是-100到100，根与根的绝对差>=1，设x为-100到100 - 1的整数，且x1<x2，f(x1)×f(x2)<0，则[x, x+1]间只有一个根。

代码如下：

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;typedef long long LL;double f_check(double x, double a, double b, double c, double d) {return a * x * x * x + b * x * x + c * x + d;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);double a, b, c, d, L, R, mid = 0, Lval, Rval, cnt = 0, eps = 1e-4;cin >> a >> b >> c >> d;for (LL i = -100; i <= 100; ++i) {L = i, R = i + 1, mid = 0;Lval = f_check(L, a, b, c, d), Rval = f_check(R, a, b, c, d);if (Lval == 0) {++cnt;cout << fixed << setprecision(2) << L << ' ';} else if (Lval * Rval < 0) {while (fabs(R - L) > eps) {mid = (L + R) / 2.0;if (f_check(mid, a, b, c, d) * Rval <= 0)  L = mid;else  R = mid;}cout << fixed << setprecision(2) << L << ' ';++cnt;}if (cnt == 3)  break;}return 0;
}

写if else if的原因是，若Lval * Rval <= 0，直接二分找根，有三种情况，第一种情况Lval是根，第二种情况[Lval + 1, Rval - 1]中有根，第三种情况Rval是根，如果当前是第三种情况，下次遍历的Lval * Rval为0是第一种情况，会重复输出根，所以要判断当Lval为0（Lval是根）或Lval * Rval < 0（[Lval + 1, Rval - 1]中有根）才输出根。

一个范围内有多个解且具有单调性，每个解之间绝对值>=k，什么范围有解确定，x + k为该范围内的数，则每次二分查找有解的区间[x, x+k]，注意不要重复输出一个解。