利率的计量

当我们谈论年利率的时候，根据复利频率的不同，会有不同的表现形式。

比如，假设年利率是10%，那么可以是一年按10%复利一次，也可以是半年按5%复利两次，还可以是每3个月按2.5%复利4次。

假设将A资金投资n年。如果利率是按年复利的，那么投资的终值为：

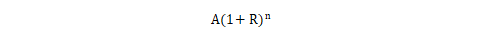
如果利率是对应于一年复利m次，那么投资终值为：

下面用Python程序来对复利m次的投资终值进行一个模拟操作。
假设初始投资 A 为100元，年利率 R 为10%，投资1年（n值），复利次数从1到15（m值）。

从图中可以看到，随着复利频率的增加，投资终值趋近于一个极限。
可以从数学上进行证明，当复利频率趋于无穷大的时候，投资的终值为：

其中e=2.71828。这种情况下对应的利率被称为连续复利（continuous compounding）利率。

在实际情况下，由于每天计算复利的频率非常高（每年复利365次）​，非常接近于连续复利，因此可以认为普通复利的计算方法与连续复利的计算方法是等价的。

对一笔资金，以利率R连续复利n年，相当于乘以e^Rn；
反过来我们可以计算贴现值。什么是贴现值呢？未来到手的资产在当前值多少钱，就是某资产的贴现值。一笔n年后的资金如果要计算贴现值，则以利率为R按连续复利进行贴现，相当于除以e^Rn。

假设Rc是连续复利利率，Rm是与之等价的每年m次复利利率。可以得到：

即：

用这个公式可以对m次复利利率和连续复利利率进行相互转换，公式如下：