四元素、旋转矩阵与旋转向量
算法
文章目录
- 算法
- 摘要
- 旋转矩阵
- Rodrigue旋转向量
- 四元素
- 参考链接
摘要
本文介绍了三种表示三维空间旋转的方法:旋转矩阵、Rodrigue旋转向量和四元素。旋转矩阵通过绕X、Y、Z轴(分别对应俯仰角、偏航角、翻滚角)的乘积构建正交矩阵;Rodrigue旋转向量用旋转轴和角度表示旋转,并推导了旋转向量到矩阵的转换公式;四元素作为复数域的扩展,通过实部和虚部描述旋转。文章还提供了相关参考链接,为读者深入学习提供了资源。这三种方法各有特点,在计算机视觉和机器人领域有广泛应用。
旋转矩阵

1、坐标系绕X轴旋转ϕ \phiϕ角(Pitch 俯仰角)

2、坐标系绕Y轴旋转θ \thetaθ角(Yaw 偏航角

3、坐标系绕Z轴旋转ψ \psiψ角(Roll 翻滚角)

整个坐标系的旋转矩阵是绕各个轴旋转的旋转矩阵的乘积。
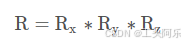
旋转矩阵必须是正交的。
Rodrigue旋转向量
设旋转向量的单位向量为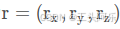 (旋转轴),模为 θ (旋转角),三维点 p 在旋转向量 r 的作用下变成p ′ :
(旋转轴),模为 θ (旋转角),三维点 p 在旋转向量 r 的作用下变成p ′ :

旋转向量转旋转矩阵:

其中

四元素
四元素是三维复数域,可表示为Q=[x,y,z,w]或Q=w+xi+yj+z*k,其中w是实部,[x,y,z]是虚部,[i,j,k]是虚轴,四元数是单位向量。描述了旋转轴r = 
和角θ \thetaθ,对应的四元数为:

两个四元素叉乘的物理含义:先绕第一个四元素旋转,再绕第二个旋转。
参考链接
https://blog.csdn.net/tchenjiant/article/details/51485745
https://blog.csdn.net/hongbin_xu/article/details/78929006
https://zhuanlan.zhihu.com/p/93563218
